引言

接續前一篇的投影介紹，今天要正式來應用線性代數中的投影公式，跨過第一道門檻—「將物體三維座標轉成二維座標」。

概念

這邊我直接放一張概念圖，更好來介紹投影公式：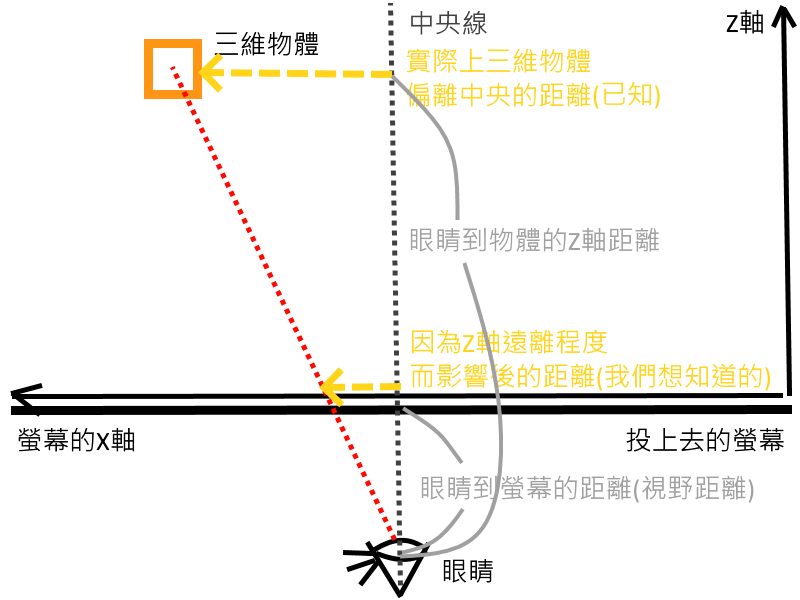

大家可以從這張圖看到兩點：

1. 原本三維物體的Z分量，被轉換為X分量變化快慢(Z分量愈大，離觀察者愈遠，X分量變化愈慢。明明移動很多，在螢幕上只移動一點點)，因此可捨棄掉Z座標，目標達成！

2. 物體、中央線、眼睛、螢幕形成了兩層直角三角形，一共有四組重要的邊，分別是：

   • 眼睛到螢幕的距離(取名為esd)
   • 眼睛到物體的Z軸距離(取名為eod)
   • 已知的，實際上三維物體偏離中央的距離(ax)
   • 想知道的，因Z軸偏離距離而影響的X軸偏移距離(bx)

   我們想知道的，就是那個在螢幕上的X軸偏移距離(bx)，這代表著轉換後二維座標的X座標，最後我們只要同理類推就可以知道二維座標的Y座標，而得知整個二維座標，這樣一來目標就達成啦！

公式

我們直接由那四個資訊，加上那兩層直角三角形的關係(小直角三角形的高比上大直角三角形的高，等於小直角三角形的底比上大直角三角形的底，也就是相似三角形的關係啦～)，可以得出公式：

移項一下：

求得bx啦！也就是投影後的二維X座標哦，同理Y座標：

這樣也求得by了，也就是我們投影後的二維座標是：(bx, by)

只要將每個三維座標點的(bx, by)一一繪製到螢幕上，就顯示出了原三維物體的二維投影啦～

總結

經過了這些推導與觀察，大家可以發現投影的概念是將想要捨棄的Z分量，轉為X,Y分量移動的難易程度。

這個在生活中也是很好觀察的，相信大家都有抬頭看過飛機飛在空中過吧！不知道大家有沒有發現，飛機速度明明那麼快，為什麼我抬頭看的時候看起來飛得好慢...

其實不是飛機真的飛得慢，只是飛機離我們太遠(Z軸方向距離遠)，我們的觀測平面上(X,Y平面)飛機移動的程度就會非常小。

這就是投影的原理，直接模擬這種特性，讓人的大腦誤以為二維中存在三維物體，只是一種錯覺罷了～