真實世界的物體，在針孔相機成像模型下，其座標轉化的過程可以以下列式子表示: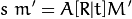

or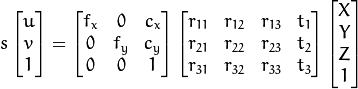

(X,Y,Z)是根據世界坐標系所描述的一個3D點的x,y,z座標
(u,v)是以像素為單位的投影點座標
A是相機矩陣，或是內參數矩陣
(cx,cy)是principal point通常是影像中心
fx,fy 是焦距以像素為單位

[R|t]是旋轉平移矩陣，也被稱之為外參數矩陣，它用於描述靜態場景下相機的運動，反之亦然，也可以解釋為相機前方物體的剛性運動。

一般來說我們可以透過上面式子來表示針孔成像的部分，然而真實影像因為鏡片光學原理的關係會有畸變，而為了校正這部分的變形而又有許多畸變參數。然而這部分牽扯到相機校正在此不予贅述，故我們先假定我們的相機沒有任何畸變。

首先根據上面式子搭配以下程式碼。

#include<opencv2/core/core.hpp>
#include <opencv2/core/types.hpp>
#include<iostream>

int main() {
	cv::Point3d pointA =  cv::Point3d(0, 0, 800);


	cv::Mat cameraMatrix_out = (cv::Mat_<double>(3, 4) << 1, 0, 0, 0,
														  0, 1, 0, 0,
														  0, 0, 1, 0);

	cv::Mat cameraMatrix_in = (cv::Mat_<double>(3, 3) << 800, 0, 400,
														 0, 800, 300,
														 0, 0, 1);

	cv::Mat image_place = cameraMatrix_in * cameraMatrix_out*(cv::Mat_<double>(4, 1) << pointA.x, pointA.y, pointA.z, 1);

	std::cout << image_place<<std::endl;

	std::cout << image_place/image_place.at<double>(2,0) << std::endl;
	return 0;
}

這段程式碼有幾個假設，我假設相機的原點就是世界座標的原點，並且有一個點在我的前方(Z軸的方向)800個單位遠。然後相機成像平面為800X600的解析度且距離相機的原點800個像素單位遠。(注意這裡的像素單位並沒有物理意義並不是一個像素單位等校於1cm或是1mm)
所以這個點剛好與影像中心重疊，就會剛剛好成像於影像中心。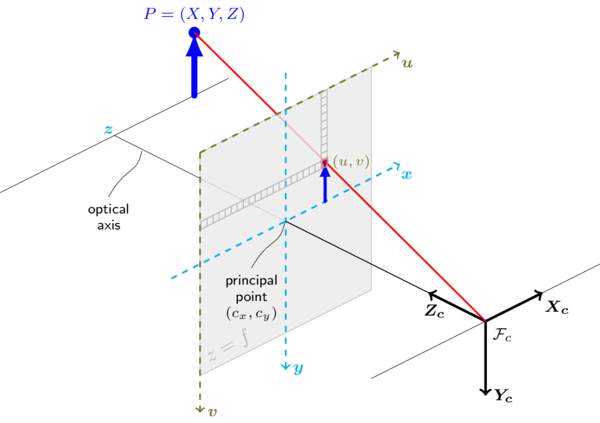

你可以觀察到，透過相機原點向四個成像平面的頂點的射線，可以形成一個四角椎的場景。而出現在這個場景裡面的物體才有機會出現在成像平面上而被感光元件所記錄。

接者你可以嘗試改變[R|t]觀察其變化，你可以說是你改變了相機的位置，或是換句話說相機沒有動，但場景內的點移動了。