上一篇的最後，我們透過修改[R|t]裡面的值可以觀察其變化，然而我並沒有教你怎麼修改。
這邊就讓我來說說幾個簡單的旋轉矩陣的表示方法。

在三維座標軸的旋轉中，可以將旋轉分解成分別對X軸、Y軸與Z軸做旋轉。假設對X、Y、Z的旋轉角度分別是Θx、Θy、Θz。其旋轉矩陣可以表示為下: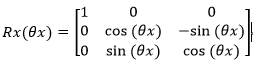

	cv::Mat rotation_x = (cv::Mat_<double>(3, 3) << 1, 0, 0,
													0, cos(AngleX * CV_PI / 180), -sin(AngleX * CV_PI / 180),
													0, sin(AngleX * CV_PI / 180), cos(AngleX * CV_PI / 180));

	cv::Mat rotation_y = (cv::Mat_<double>(3, 3) << cos(AngleY * CV_PI / 180), 0, sin(AngleY * CV_PI / 180),
													0, 1, 0,
													-sin(AngleY * CV_PI / 180), 0, cos(AngleY * CV_PI / 180));

	cv::Mat rotation_z = (cv::Mat_<double>(3, 3) << cos(AngleZ* CV_PI/180), -sin(AngleZ * CV_PI / 180), 0,
													sin(AngleZ * CV_PI / 180), cos(AngleZ * CV_PI / 180), 0,
													0, 0, 1);

而有了這三個分別對三個軸的旋轉我們就可以透過矩陣的乘法得到最後的旋轉矩陣，而在
的前提下我們可以組合出我們的旋轉矩陣以下列程式表示，並透過修改點的位置來簡單驗證我們的旋轉是否合理。
(注:這裡組合的順序會影響最後旋轉矩陣的結果，矩陣乘法沒有交換律)

#include<opencv2/core/core.hpp>
#include <opencv2/core/types.hpp>
#include <math.h>
#include<iostream>

int main() {
	cv::Point3d pointA =  cv::Point3d(0, 0, 1);

	double AngleX=0, AngleY=90, AngleZ=0;

	cv::Mat rotation_x = (cv::Mat_<double>(3, 3) << 1, 0, 0,
													0, cos(AngleX * CV_PI / 180), -sin(AngleX * CV_PI / 180),
													0, sin(AngleX * CV_PI / 180), cos(AngleX * CV_PI / 180));

	
	cv::Mat rotation_y = (cv::Mat_<double>(3, 3) << cos(AngleY * CV_PI / 180), 0, sin(AngleY * CV_PI / 180),
													0, 1, 0,
													-sin(AngleY * CV_PI / 180), 0, cos(AngleY * CV_PI / 180));
	
	cv::Mat rotation_z = (cv::Mat_<double>(3, 3) << cos(AngleZ* CV_PI/180), -sin(AngleZ * CV_PI / 180), 0,
													sin(AngleZ * CV_PI / 180), cos(AngleZ * CV_PI / 180), 0,
													0, 0, 1);

	cv::Mat result = rotation_y * rotation_x * rotation_z;
	std::cout << "result1/n" << result << std::endl;

	cv::Mat cameraMatrix_out= cv::Mat::eye(3, 4, CV_64FC1);
	result.copyTo(cameraMatrix_out.rowRange(0, 3).colRange(0, 3));

	std::cout << "cameraMatrix_out/n" << cameraMatrix_out << std::endl;


	cv::Mat space_place = cameraMatrix_out*(cv::Mat_<double>(4, 1) << pointA.x, pointA.y, pointA.z, 1);

	std::cout << space_place<<std::endl;
	return 0;
}

下一篇我想嘗試整理旋轉向量的表示法.........並帶入opencv::Rodrigues()