我們昨天提到了兩個重要的知識，分別出現在我們超級簡化流程裡的二、三步驟，一個是用來判定函式的好壞的損失函式，一個是要讓我們持續逼近最好的函式的梯度下降法。
今天會主攻損失函式！ＧＯＧＯ！

在機器學習中，損失函式有非常多種類，例如：均方誤差(Mean square error，MSE)、平均絕對值誤差(Mean absolute error，MAE)、交叉熵(cross-entropy)等等。

今天只會介紹到比較基礎好懂的MAE，也是常用在做回歸相關案例的損失函式。

平均絕對誤差(Mean Absolute Error，MAE)

平均絕對誤差也可以稱作L1損失。光看到這個名詞「平均絕對誤差」，我們就可以從中推敲他的公式，一定有是「絕對值」也有「平均」的概念在裡頭。
先放上MAE公式給大家瞧瞧：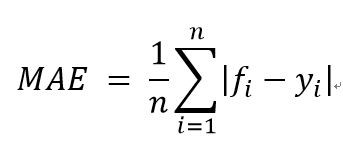

沒錯沒錯，果真有絕對值和要找平均值！
而參數們個別代表

1. n : 資料數
2. fi : 預測值
3. yi : 實際值

JOHN國為例

id | price | sqft_living
------------- | ----------
1 | 500000 | 55
2 | 275000 | 27
3 | 360000 | 33
4 | 780000 | 70
5 | 145000 | 13
6 | 280000 | 26
7 | 860000 | 89
8 | 200000 | 21
9 | 90000 | 10
10 | 680000 | 67

也就是說現在n = 10，而各個price就是yi。

實際做做看：假設我們現在從函式池子選到 fi(預測的價格) =6000 * x(sqft_living) + 10000

先把各個sqft_living的fi算出來：
id | fi | sqft_living
------------- | ----------
1 | 340000 | 55
2 | 172000 | 27
3 | 208000 | 33
4 | 430000 | 70
5 | 88000 | 13
6 | 166000 | 26
7 | 544000 | 89
8 | 136000 | 21
9 | 70000 | 10
10 | 412000 | 67
然後開始計算MAE：
id ||fi - yi|| sqft_living
------------- | ----------
1 | 160000 | 55
2 | 103000 | 27
3 | 152000 | 33
4 | 350000 | 70
5 | 57000 | 13
6 | 114000 | 26
7 | 316000 | 89
8 | 64000 | 21
9 | 20000 | 10
10 | 268000 | 67
那麼這個函式所算出來的MAE=160,400

光是只有一個函式我們並不會知道它到底好不好，所以我們拿之前在【Day 04】超級基礎的機器學習－Linear Regression 介紹（1/2）用程式算出來的最佳解來重新算算看。

最佳解試試看：fi2 = 9987 * x + 6531

同樣地先計算出各個fi2
先把各個sqft_living的fi算出來：
id | fi2 | sqft_living
------------- | ----------
1 | 555816 | 55
2 | 276180 | 27
3 | 336102 | 33
4 | 705621 | 70
5 | 136362 | 13
6 | 266193 | 26
7 | 895374 | 89
8 | 216258 | 21
9 | 106401 | 10
10 | 675660 | 67
然後開始計算MAE：
id ||fi2 - yi|| sqft_living
------------- | ----------
1 | 55816 | 55
2 | 1180 | 27
3 | 23898 | 33
4 | 74379 | 70
5 | 8638 | 13
6 | 13807 | 26
7 | 35374 | 89
8 | 16258 | 21
9 | 16401 | 10
10 | 4340 | 67
那麼這個函式所算出來的MAE=25,009.1

可以看得出來我們用程式找到的最佳解所算出來的MAE會小於隨便撈的函式，所以MAE越小，表示函式越好！

問題1：為什麼要取平均？

因為在我們的訓練資料中不會只有一筆，可能會有成千上萬筆，所以如果取平均的話，可以看出大多數的誤差大致落在哪裡。

隨便舉一個例子：今天有100筆資料，和有一個隨便的方程式fi，且fi - yi(誤差)除了異常值為1000外，其他都是10
如果不取平均：1990
如果取平均：19.9
可以從取平均後的19.9觀察到相對於不取平均的1990，我們更可以看出大部分的誤差值分布。

問題2：為什麼要加絕對值？

因為我們的資料不只一筆，所以可能會有的誤差是正，有的誤差是負，會有機會抵銷，這樣會導致機器判斷錯誤，找到比較不好的函式。
如：現有兩筆資料，有一筆誤差是+100，有一筆誤差是-100，這樣當我們加起來的時候誤差會變為0，導致機器判定此函式為最佳解，但事實上不是。

今天比較忙碌，非常匆忙的完成這篇介紹，尤其是在計算各MAE的時候花了一些時間，我會在不斷地再看幾次，如果有打錯字或者數值算錯還先請包涵，一定會找時間改正！

今天完成了MAE的介紹，明天將開始介紹Gradient Decent，敬請期待囉！