昨天講完損失函數的式子，以及實際操作了一遍數學，今天要來分享Gradient Decent拉！
我們要先補充一個名詞，叫做優化器！

優化器(optimizer)

優化器是在coding中才會碰上的問題，因為優化器有很多很多種類可以挑選，如GradientDescentOptimizer、AdagradOptimizer、RMSPropOptimizer、AdamOptimizer等等，選擇一個適合的優化器也是一門學問！
而優化器具體來說在幹嘛呢？透過優化的方法，對目標函數進行優化進而找到最好的函式，而優化的方式就是要最小化損失函數。
也就是說，優化器要用來找到損失函數最小的函式！

今天只會提到最常用也最簡單的優化方法-Gradient Descent

梯度下降(Gradient Decent)

先來看一張圖：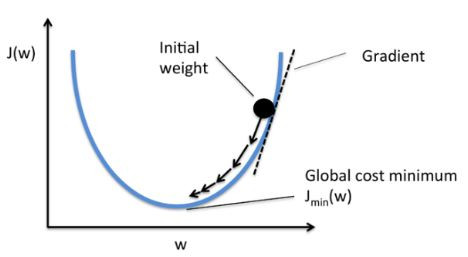

圖片出處
之前有提到梯度下降法將會帶領機器找到擁有最小損失函數的那個函式！而從上方這張圖可以看到，一開始我們會選擇一個隨便的位置，然後開始做Gradient Decent，那Gradient Decent將會帶我們找到有最低loss的那個點。

梯度下降的數學理論

我們先以更簡單的式子y = w * x去解釋，我們可以把梯度下降的式子寫成：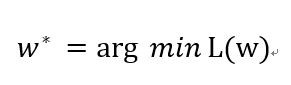

w* : 更新後的參數
arg min : 從後面的式子取到最小值時，裡面變量的取值。
L() : 損失函數

那實際上到底要怎麼找呢？
首先我們會找到一點w0(起始位置)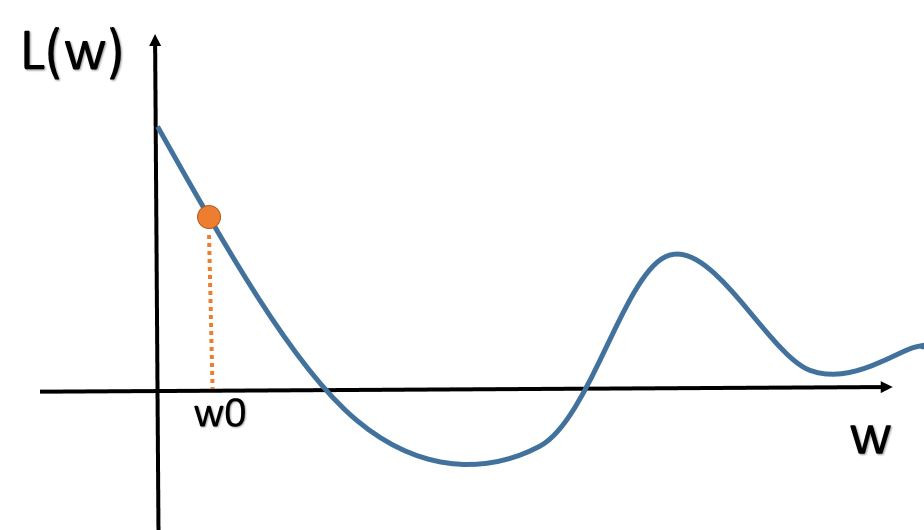

然後，對L()做一次微分，dL/dw|w=w0。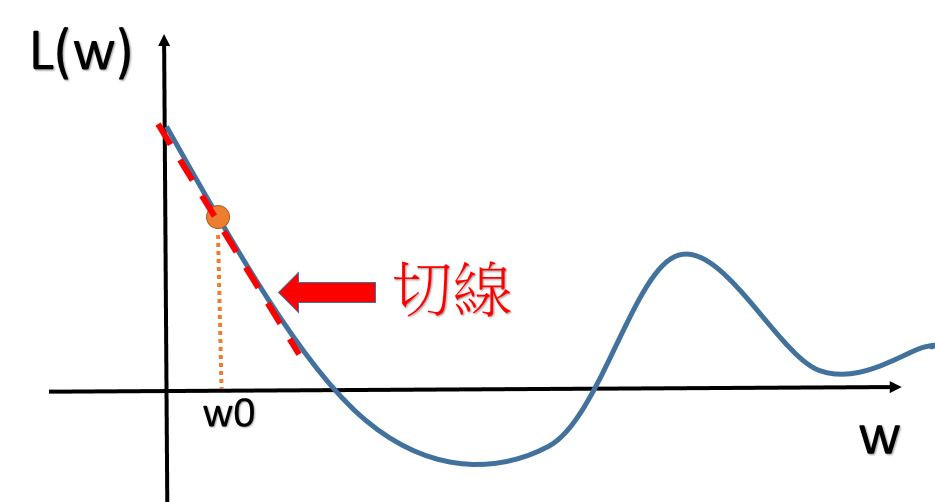

機器會藉由微分出來的結果是正還是負，去更新w，像上圖中，斜率(dL/dw|w=w0)算出來會是負的(左高右低)，那麼機器就會知道新的w要往右邊走(所以η前面才會是負號)，所以w0要增加；反之，如果(dL/dw|w=w0)算出來會是正的(左低右高)，那麼就會往左邊走。
而式子會變成：　w = w0 - η × (dL/dw|w=w0)

其中的η意思是學習率(Leraning Rate)。
學習率就是學習的速度，如果學習率越高，圖上走一步的步伐就會越大，例如今天w0=10，(dL/dw|w=w0)=-10，η=0.01，那麼新的w就會等於10.1；那如果 η=0.1，新的w就會等於11。

最後機器會一直重複：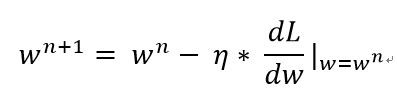

那會到什麼時候呢？當微分值等於0的時候就會停止更新，因為這時候(dL/dw|w=wn)這項會是0。
那這代表什麼意思？當微分值等於0的時候，就代表我們到最低處了！
也就是會到這裡：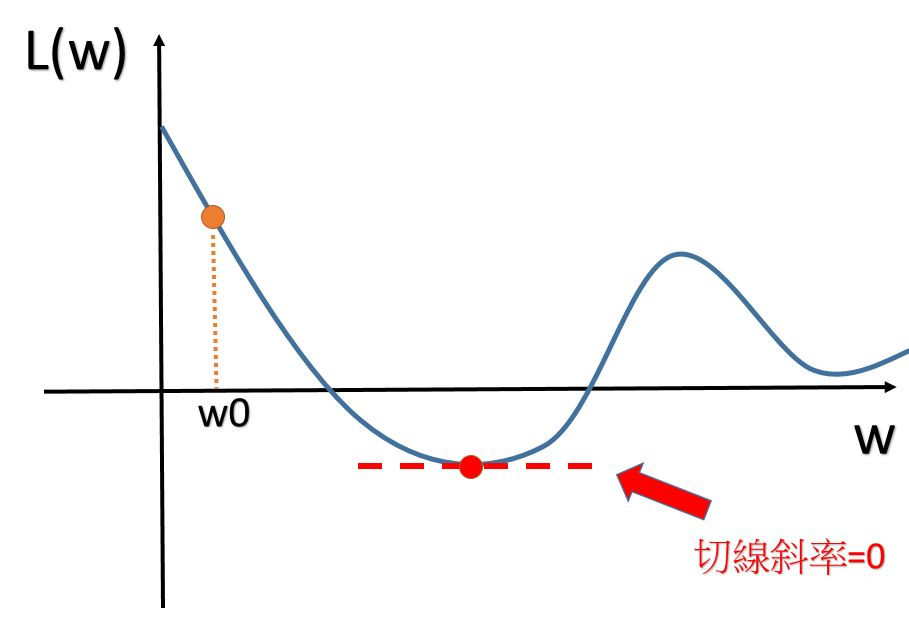

這時候我們就找到讓損失函數最小的地方，也就是這時候的w*是我們要的答案！

學習率大小問題補充

學習率越大越好嗎？不是代表學得越快？
先看下這張圖：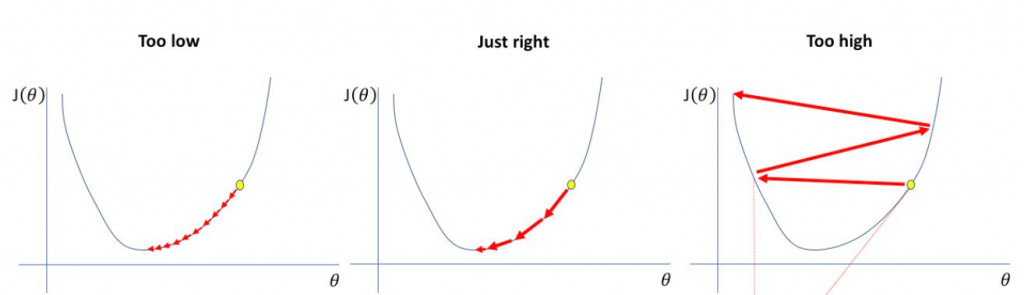

圖片出處
當在做梯度下降法時，學習率如果設的過大，就會造成右邊的圖那樣，會無法跳到最低點，而是左右左右亂跳。
那如果太小呢？雖然可以跑到最低點，但是會變得非常非常耗時，所以在訂定學習率大小時也要特別注意。

因為最近學校事情比較多，今天的文章也打得比較急一些，以防有錯字，會在發文後再次檢查的！
今天把Gradient Decent的流程帶入，並以較基礎數學的方式進行介紹，明天會開始介紹python的安裝！然後開始介紹會使用到的重要套件！