路遙知碼力，日久練成精- 只要在程式之路鑽研的夠深，便能夠充分發揮程式碼的力量; 練習的日子夠久，便能夠練成寫出精簡代碼的能力。

其實這標題來自某八○年代卡通的哏。
那麼為什麼我稱遞迴函數為黑魔法呢?
首先就要來了解一下到底什麼是遞迴函數了。

(圖片來源: 截自動畫「魔法咪路咪路」)

遞迴函數工作原理?

遞迴函數就是在一個函數裡面調用函數自己稱為遞迴函數，
為什麼要在函數裡呼叫自己呢?
假設我們本來想要解一個比較複雜的問題但不會解，
這時我們想到說如果我們會解一個與原本問題相同類型的小問題，
就可以解開原本的大問題了。
講起來非常的抽象，我們看一些例子吧。

範例21-1: 階乘

在數學上，n階乘定義為1到n之間所有自然數的乘積，即
n! = 1*2*3*…*(n-1)*n
有經驗的人可能直覺會想到可以用for迴圈來計算，
這邊我們用遞迴函數的思想來計算n階乘。
假設我們定義一個函數fact(n)，它的效果就是計算n階乘。
上個圖示說明一下: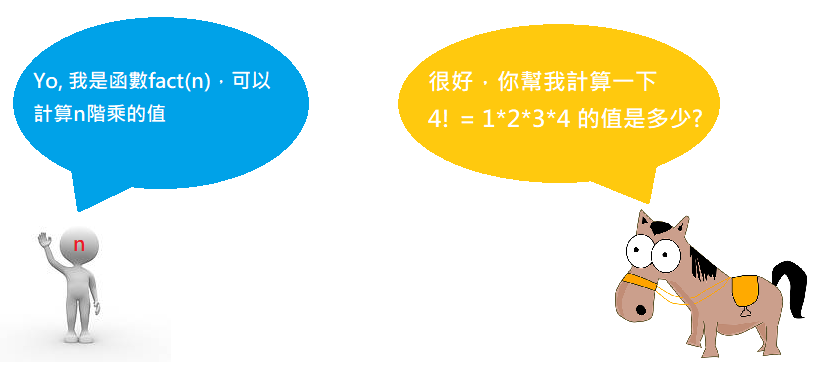

左邊的人代表fact(n)這個函數，
右邊的馬兒代表使用者，他去呼叫了fact(4)這個函數，
但是對於fact(n)這個人來說，
他其實也不知道完整的運算過程是怎麼樣的，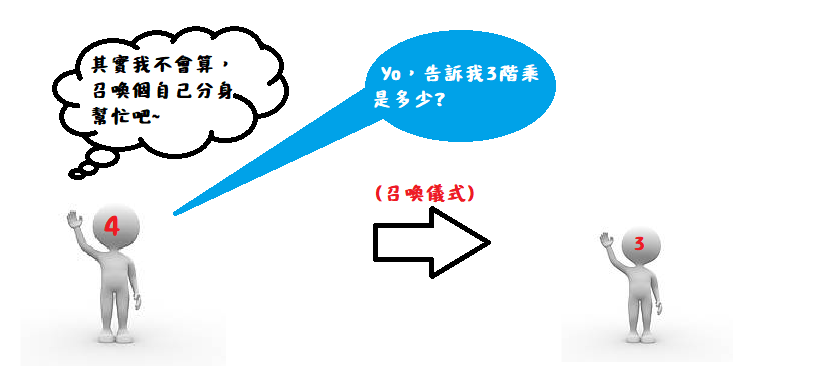

但是fact(n)靈光一閃，他想到因為n! = 1*2*3*…*(n-1)*n = (n-1)! * n，
如果可以知道(n-1)階乘是多少的話，
那麼其實只要把(n-1)階乘的答案再乘上n就是n階乘了，
於是他便呼叫自己的小分身出來，
他的分身跟自己能力相同(都是計算階乘)，但是能力稍微弱化一些:

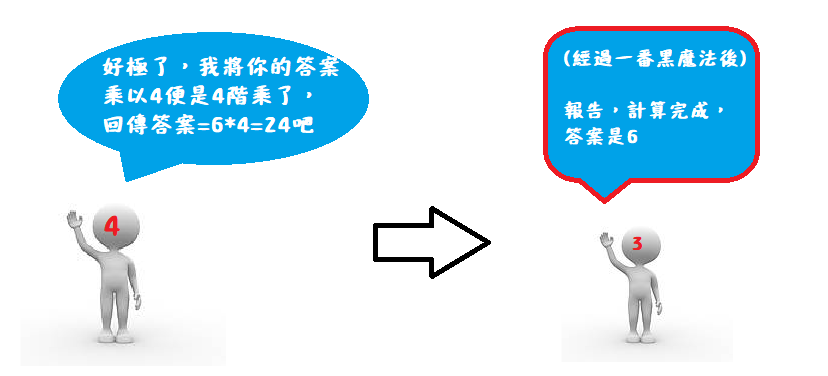
透過遞迴呼叫「小分身」幫fact(4)算出3階乘=6，
fact(4)只要把它拿到的答案再乘上4就是答案了。

讓我們再想想，fact(4)不知道完整的運算過程，
難道fact(3)就知道嗎?
他當然也不知道，但是他知道做一樣的事情，也去呼叫「自己的分身」: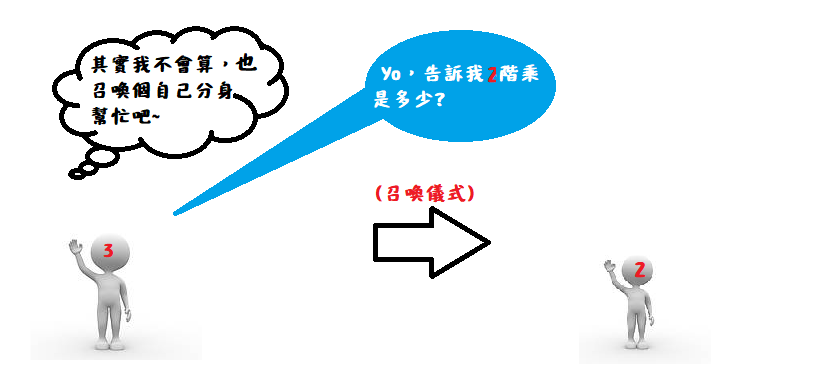

接下來的事大概就可以想像了，
fact(2)會告訴fact(3)說2階乘答案是2，
fact(3)他只要把2乘上3就得到6這個答案了。

這大概就是整個遞迴的原理了，
若把每個fact(n)想像成單獨的個體的話，
他們都不知道答案怎麼來的，
可是卻能夠透過上、下合作而得到正確的答案。
另一個比喻是說，你可以把fact(n)想成是fact(n-1)的「直屬主管」，
對於每個人來說，他們只需要將分內工作做好回傳給直屬主管就好，
其它事就不用多管了
儘管無法一窺全局，仍然可以知道答案，
因此我覺得遞迴就像「黑魔法」。
想法直接打成程式如下:
(階乘的英文是factorial，這邊函數名取簡寫叫fact)

def fact(n):
    return fact(n-1)*n
    
print(fact(4))

但目前這支程式應該會出錯，
還忽略一個重要要素不知讀者們發現了嗎?

遞迴函數兩大要素: 「遞迴關係」與「終止條件」

相信看了上例應該大家對遞迴有一些概念知道如何運作了，
構成遞迴函數的兩大要素便是「遞迴關係」與「終止條件」，

1. 遞迴關係，也就是本文所稱的「黑魔法」，指函數之間大問題與小問題之間的關係，如上例中的fact(n)=fact(n-1)*n即是一例。
2. 終止條件，指遞迴關係的停止條件，例如上例的條件應為fact(1)=1。

回顧剛剛fact(3)呼叫fact(2)的場景，
這個動作總要有停下來的一天，
否則fact(1)會去問fact(0)0階乘是多少，
fact(0)又會去問fact(-1)-1階乘是多少，
如此下來沒完沒了。

因此，範例21-1的正確程式為:

def fact(n):
    if n==1:
        return 1
    return n*fact(n-1)

不過我們是學精簡程式的，此程式可進一步化簡為:

def fact(n):
    return 1 if n==1 else n*fact(n-1)

現在再去呼叫print(fact(4))已能夠得到正確結果24。

範例21-2: 河內塔

河內塔問題是遞迴函數中一個非常經典的例子，
問題為有A, B, C三個石柱，
其中A石柱有n個由大小不一的圓形金片，
由大至小的依序疊在A石柱上，如圖所示: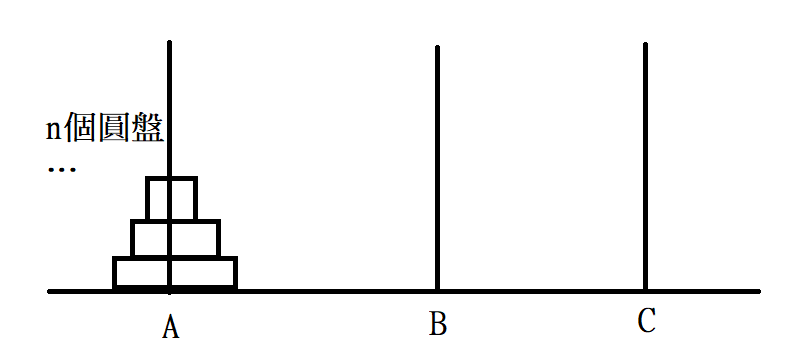

規定一次只能移動一個金片到另一個石柱上，
而且小的金片永遠在大的金片上面，
那麼請問我們如何將所有金片移動到C石柱上呢?

首先假設我們會解小一點的問題，
即我們知道該如何搬動n-1個金片到另一個石柱上，
那麼整個問題其實可以拆解成三個步驟:

1. 將A石柱的前n-1個金片搬到B石柱上
2. 將A石柱最大的金片搬到C石柱上
3. 將B石柱的n-1個金片搬到C石柱上

最後，別忘了設置終止條件，
當n=1時，直接把A石柱的金片搬到C石柱上即可。
我們假設金片由小到大編號為1，2，…，n，
我們實際實作函數演示要如何搬金片可以達到目的，
程式如下:

def hanoi(n,a,b,c): #將石柱a的n個圓盤移到石柱c(b為輔助)
    if n==1:
        print(f"將1號金片由{a}石柱移動到{c}石柱")
    else:
        hanoi(n-1,a,c,b)
        print(f"將{n}號金片由{a}石柱移動到{c}石柱")
        hanoi(n-1,b,a,c)
        
hanoi(4,'A','B','C')

結果為:

將1號金片由A石柱移動到B石柱
將2號金片由A石柱移動到C石柱
將1號金片由B石柱移動到C石柱
將3號金片由A石柱移動到B石柱
將1號金片由C石柱移動到A石柱
將2號金片由C石柱移動到B石柱
將1號金片由A石柱移動到B石柱
將4號金片由A石柱移動到C石柱
將1號金片由B石柱移動到C石柱
將2號金片由B石柱移動到A石柱
將1號金片由C石柱移動到A石柱
將3號金片由B石柱移動到C石柱
將1號金片由A石柱移動到B石柱
將2號金片由A石柱移動到C石柱
將1號金片由B石柱移動到C石柱

範例21-3: 爬樓梯問題

此例也是經典的遞迴問題，
假設總共有n階階梯，你每次可以爬1階或2階，
你總共有幾種爬法?
例如: n=3時，
共有三種方法:

1. 每次都爬一階
2. 先爬一階再爬兩階
3. 先爬兩階再爬一階

由於每次只能爬1階或2階，
要爬到n階階梯，
一定從n-1階跨一步上來，
或者從n-2階跨兩步上來，
終止條件為n=0或n=1時，只有一種方法，
(註: 為什麼爬0階階梯算只有一種方法呢?
你可以想成是爬0階就「站在原地不動」一種方法。)
直接遞迴呼叫函數如下:

def stair(n): #注意: 執行速度非常慢
    return stair(n-1)+ stair(n-2) if n>=2 else 1

然而，這並不算一個好方法，因為很多資訊被重複計算了，
每個函數都去呼叫兩個小函數，
計算量大概是2的n次方，效率不佳。
這時，我們用迴圈從小的case往上推會是比較好的做法，
函數改寫如下:

def stair_fast(n):
    ways = [0]* (n+1) #用一個列表記錄爬到第i階階梯共幾種方法
    ways[0] = 1 # 初始條件
    ways[1] = 1 # 初始條件
    for i in range(2,n+1):
        ways[i]=ways[i-1]+ways[i-2]
    return ways[-1]

好啦，今天就教到這裡了，
總結來說，
適當的使用遞迴可以讓程式邏輯更簡單，
但不適當的使用遞迴也可能讓程式計算量爆炸。
預計明天來給大家講講遞迴中的經典- 八皇后問題，
我們明天見啦。