簡單回顧
在ML_Day13(SVM Kernel-1)有稍微介紹SVM kernel的主要觀念，簡單來說就是為了解決非線性問題，這一章節會做做一些複習並且做一點簡單練習。

使用Kernel在高維空間找到分離平面
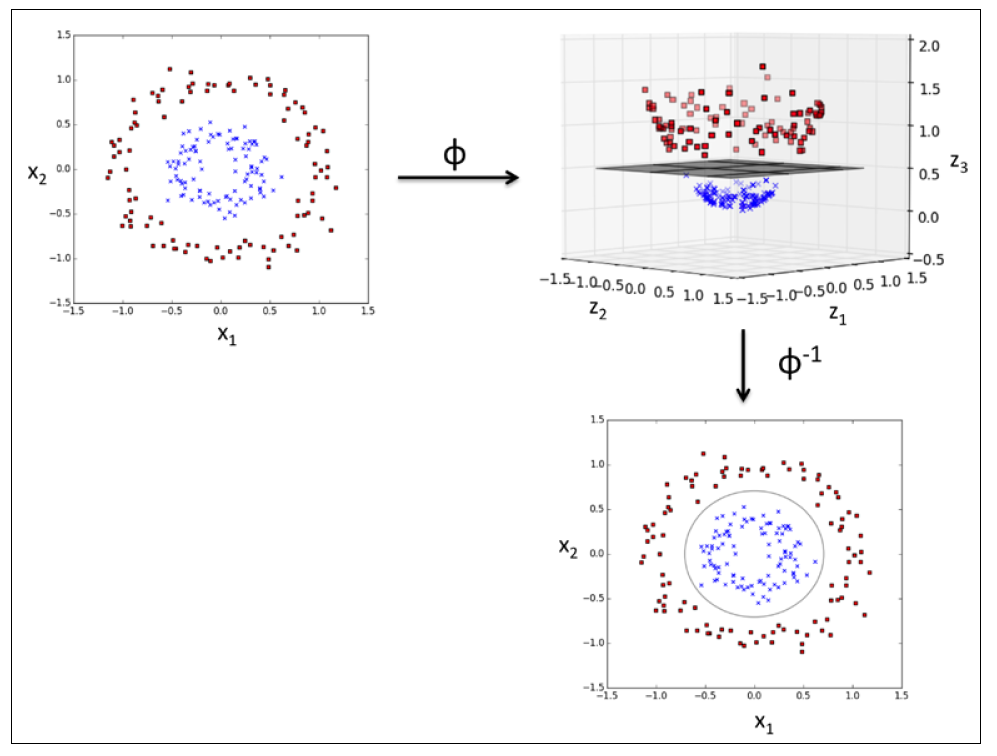
為了用SVM解決非線性問題，必須將數據資料轉換到更高維度的空間，並對這個新的空間中的數據，訓練一個線性分類器來做分類。將數據轉換到更高維度的函數我們稱為 φ

Kernel定義
k(x,l)=⟨φ(x),φ(l)⟩ = φ(x)^T φ(l)
這個k(x,l)就是一個kernel函數，表示把數據轉換後在做內積。

其中最為廣泛使用的Kernel為Gaussian kernel(ML_Day13(SVM Kernel-1)有介紹，就是相似度 f )

k(x, l) = exp(-|x-l|²/2σ²)

使用Kernel做分類
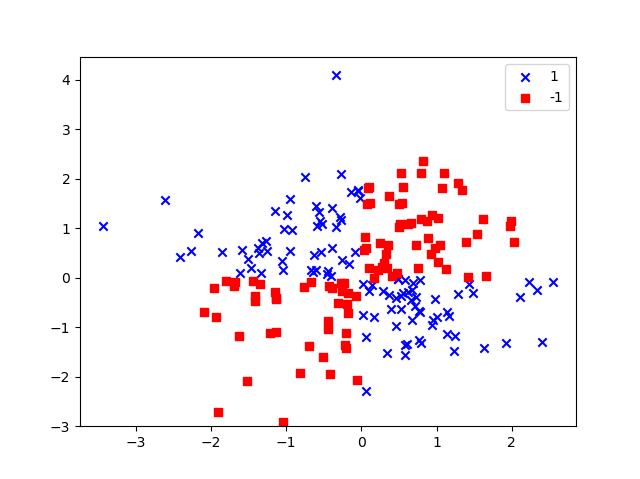
先用Numpy中的logical_xor函數產生數據，其中100筆數為1，另外100筆為-1。

X_xor = np.random.randn(200, 2)
y_xor = np.logical_xor(X_xor[:, 0] > 0, X_xor[:, 1] > 0)
y_xor = np.where(y_xor, 1, -1)
plt.scatter(X_xor[y_xor==1, 0], X_xor[y_xor==1, 1], c='b', marker='x', label='1')
plt.scatter(X_xor[y_xor==-1, 0], X_xor[y_xor==-1, 1], c='r', marker='s', label='-1')
plt.ylim(-3.0)
plt.legend()
plt.show()

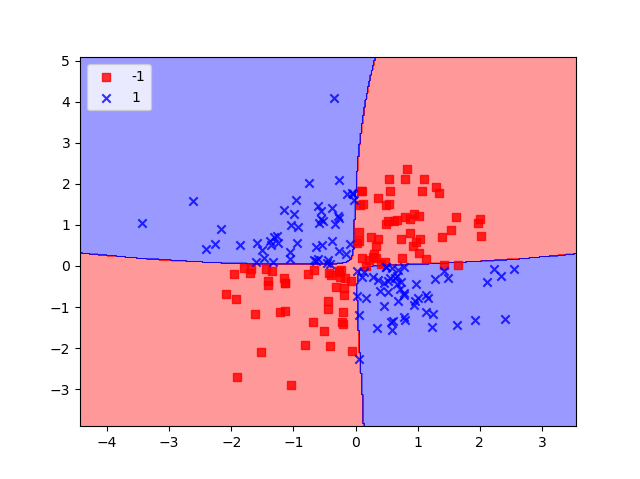
跟前一章節 一樣，使用scikit-learn提供的SVC，並將kernel換成rbf，這裡的rbf其實就是我們前面所提到的Gaussian kernel，這邊的另一個參數gamma，就是在前一章節提到的1/ 2σ²，輸出結果如下圖所示，可以看到成功的分開了整個數據。

svm = SVC(kernel='rbf', random_state=0, gamma=0.1, C=10.0)
svm.fit(X_xor, y_xor)
plot_decision_regions(X_xor, y_xor, classifier=svm)
plt.legend(loc='upper left')
plt.show()