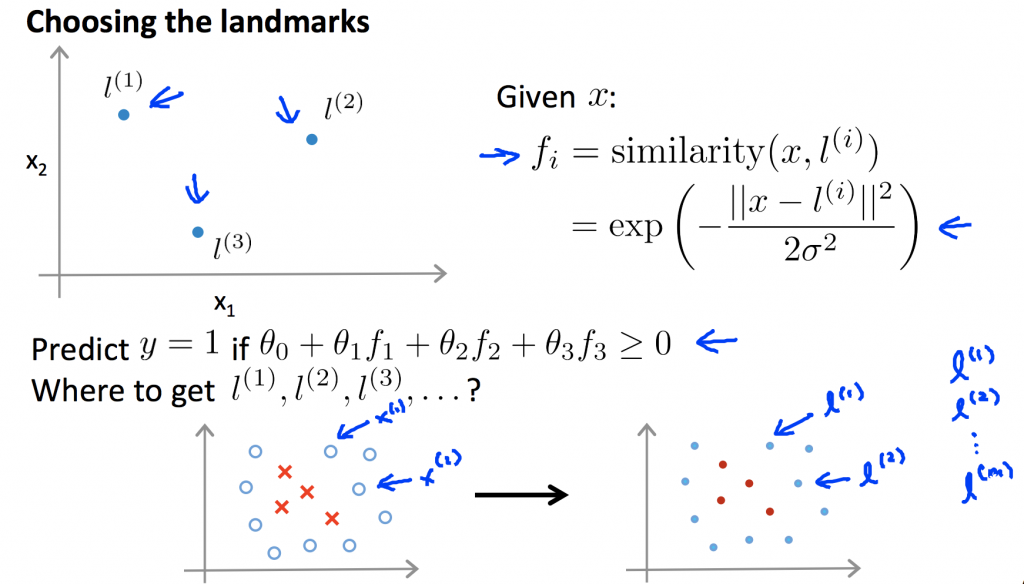
之前ML_Day11(支援向量機(Support Vector Machine, SVM))主要提到，SVM找到decision boundary讓margin最大化，就能完美分割兩類資料。但前提是這兩類資料必須是線性可分，如果像下圖一樣的資料要怎麼辦？

這就好像我們直覺地看到下面這張圖片，一條繩子上串了很多圈圈，很簡單的你就可以對他做分類：

直接在中間畫一條線，左邊是紅色圈圈，右邊是藍色圈圈。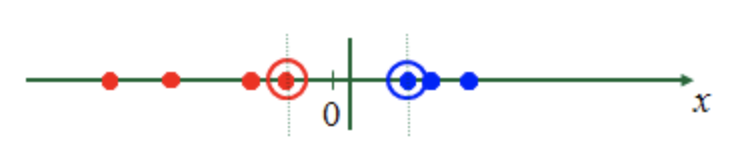

那如果是下面這張圖，不管怎麼切好像都沒辦法完全區分這兩種顏色的圈圈。這個時候靈機一動，繩子是可塑性的，我可以把它隨便彎曲，這個時候再來做分類。

如下圖所示，如果在低維度無法將兩類做區分，就必需把它轉換到更高維度的空間，再去做分類。那唯一有能力做到這件事情的就是kernel。

Kernel
以下的介紹是取自吳恩達老師機器學習課程。之前在做分類時是透過θ^T*x的正負值判斷其分類。在非線性分類，我們可以看到越複雜的方程式它的特徵量維度越高，假如在計算一張圖片時，它的pixel非常多，會造成運算量非常大，所以必須用其他特徵變量來取代原本高次方的變量。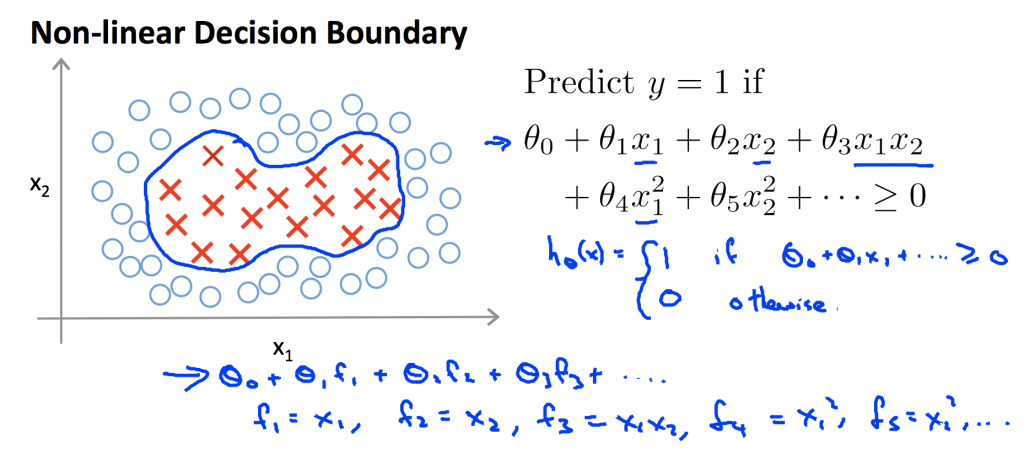

所以假設新的變量f = exp(-|x-l|²/2σ²)，代表就是相似度，比較專業的說法就是kernel，這邊所用的是Gaussian Kernel，其中l為平面上的標記點，假設目前有三個標記點（實際上可以假設很多），然後根據所給定的標記點 l 計算出相對應的f。從第二張圖可以得知，在二維平面上，如果某個點距離標記點很近，那相對應的f趨近於1；反之，如果某個點距離標記點很遠，那相對應的f趨近於0。

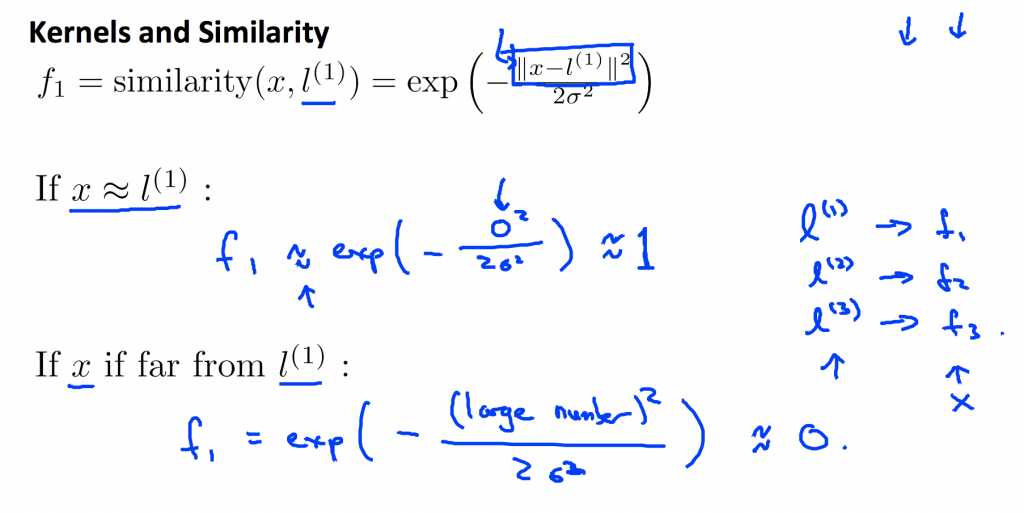
當給定一個標記點後，可以計算出在一個空間裡的點所對應到的f值，如左邊的圖，當x等於標記點時，f值剛好等於1，如果x遠離標記點，f趨近於0。

當σ越小，投影在二維平面的等高線圖也越往內縮，f形狀也越來越尖，也就是說f值變化速度較快；反之，當σ越大，投影在二維平面的等高線圖也越往外擴，f形狀也越來越鈍，也就是說f值變化速度較慢。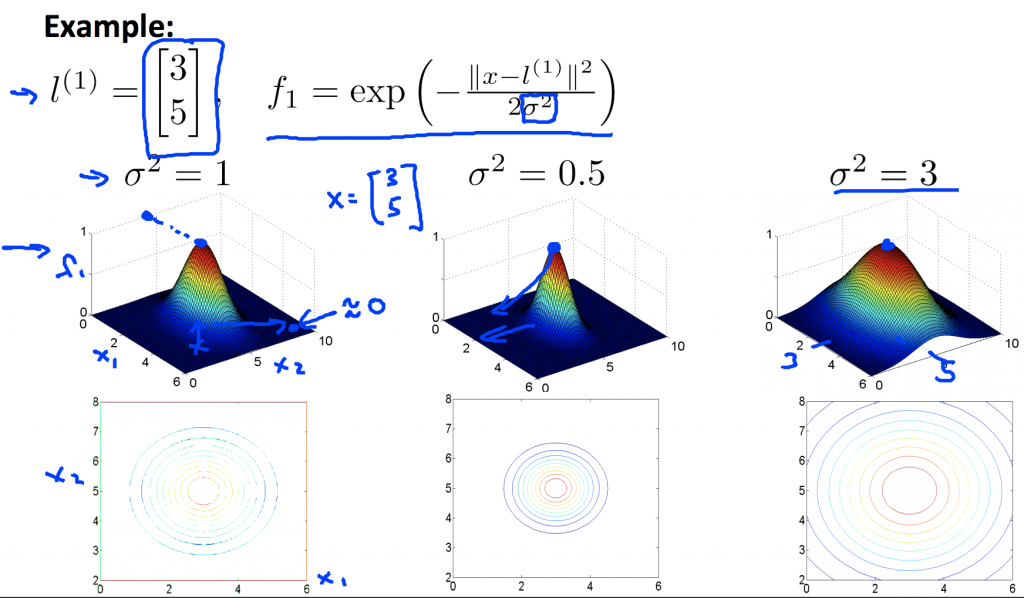

從下面的圖可以得知，假設已知θ，三個標記點，如果在這二維平面上對的多個x計算f的值，我可以得到再三個標記點內的x代入θ0+θ1f1+θ3f3是大於0，所以透過計算f我們可以針對非線性分布的資料做分類。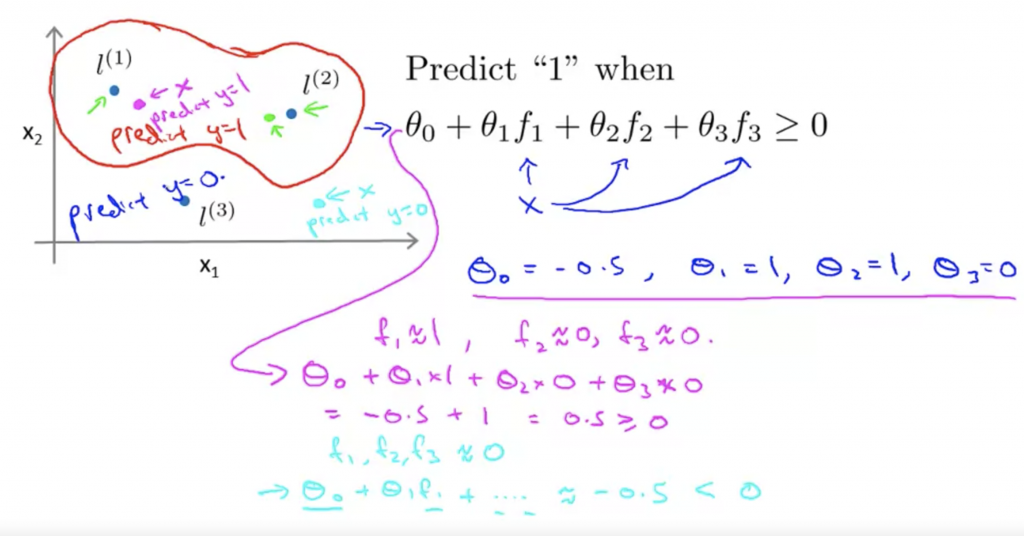

前面介紹時，我們只是隨機假設標記點，接下來我們把每一個資料點都當作是一個標記點，所以當我們在平面上所找到的一個點，都必須跟其他的點做計算，求出跟其他點的f。