在前面章節30天Flutter手滑系列 - 井字遊戲實作(Tic Tac Toe)(5)有提到，在今天開始會來嘗試加入AI到我們遊戲中，這樣才真的有玩遊戲感覺嘛。

Minimax演算法簡介

Minimax演算法常見於棋盤類遊戲，該演算法是一個零總和(zero-sum game)演算法，即一方要在可選的選項中選擇將其優勢最大化的選擇，另一方則選擇令對手優勢最小化的方法。而開始的時候總和為0。

舉一個完美的例子來說，人腦可以在井字遊戲計算出最佳解，而AI要如何評估哪一步是最佳的呢？
那就得用計算出的分數來衡量了。

• 我贏了！得10分!！！
• 我輸了，減10分。（此時對手是加10分）
• 平手。行，0分，沒有任何一方玩家在這一局獲得芳樹。

下圖是示例：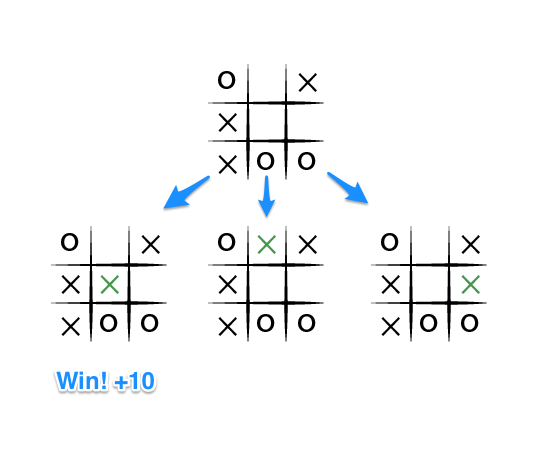

在這個圖例中，對於X來說，有三種下法，第一種會贏，其他兩種則不會結束遊戲，所以第一局的下法是一種完美走法。

但是對於O來說，假設同時也在進行遊戲，所以X得想盡辦法阻止O獲勝。這時候就得模擬一個分數，讓O去選擇較低的分數(輸掉-10或是平手0)，來作為O的最佳走法。

下圖示例：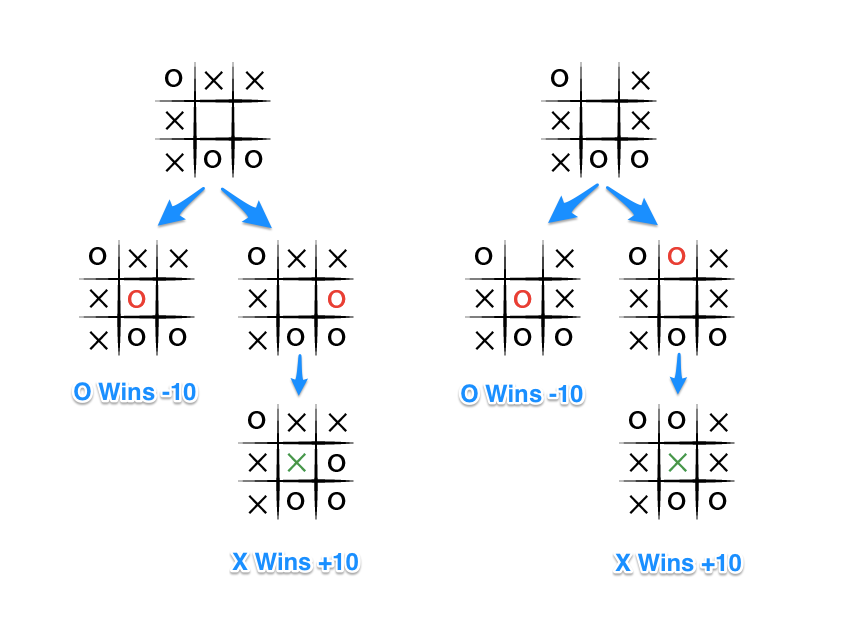

在這個圖例中，O的最佳走法是只要一步就可以贏得比賽。

Minimax演算法實現

實現這個演算法的資料結構是利用Game Tree模型。利用樹狀結構去計算出所有的結果，每個結果對應的走法就是樹的一個分枝(Branch)，每一個可能的結果就是節點(Node)，而遊戲結束的那個結果就是根節點(Root)。算法要遍例整個數，獲得節點的分數，選擇分數最高的節點。

參考資料

https://zh.wikipedia.org/wiki/%E9%9B%B6%E5%92%8C%E5%8D%9A%E5%BC%88
https://zh.wikipedia.org/zh-tw/%E6%9E%81%E5%B0%8F%E5%8C%96%E6%9E%81%E5%A4%A7%E7%AE%97%E6%B3%95
https://www.neverstopbuilding.com/blog/minimax
http://www.wukai.me/2018/03/04/minimax-alpha-beta-pruning-and-tic-tac-toe/
https://miketech.it/minimax-algorithm