前言

今天沒有前言，以後也不會有系列

1.Introduction to Optimization

如題 本章節討論的是優化ML模型
順帶一提我們的課程已經快要完成一半了
太棒了 然後我們會提到
損失函數loss functions
最佳化Gradient Descent演算法
制定Performance Metrics作業務決策
雖然的東西我現在完全看不懂 總之就是優化的一部分

2.Defining ML Models

如圖，為了優化我們的模型，我們要先定義ML模型
然後，我們要查看損失函數對於這個模型的好壞
利用梯度下降法 Gradient Descent 決定優化的方向，由損失函數定義
在環境 TensorFlow Playground下模擬模型損失的變化
最後會討論如何衡量 關鍵績效指標 Performance Metrics 優化模型

ML模型本身裡面就像是一個函數模型ｆ()，根據維基百科的解釋函數模型就如下圖XD：

現階段當我們討論監督式學習
我們透過修改模型參數使模型能夠輸出對應的答案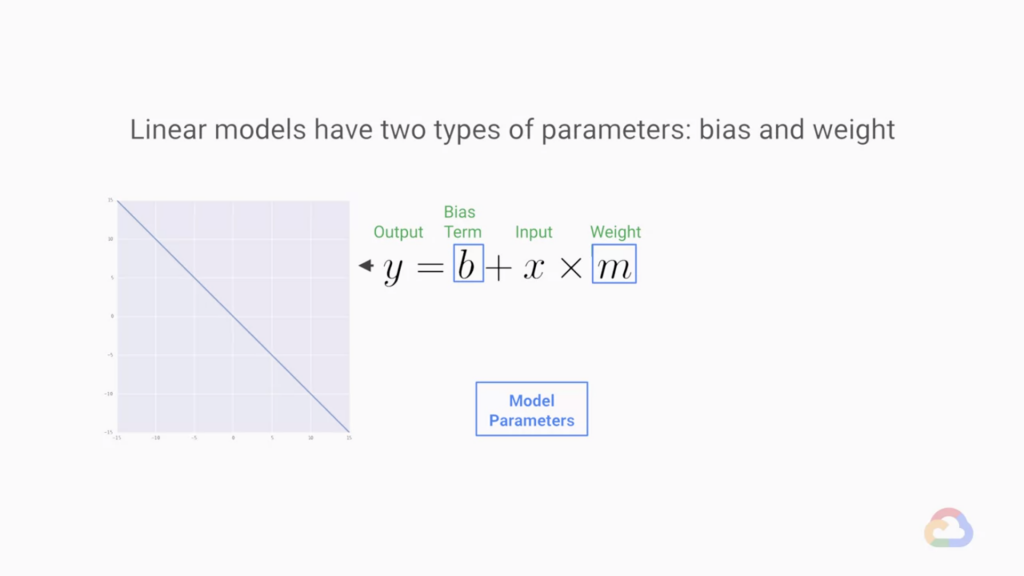

參數又分成兩種，一種是參數parameters和 超參數hyper-parameters
參數parameters：是可變的，是訓練模型時變化的參數
超參數hyper-parameters：反之超參數不可變，是順練前就決定好的參數，之後也不會改變

線性模型是最早的ML模型之一。
至今它們仍然是重要且廣泛使用的模型類別。

我們所做的就是不斷的調整參數好讓我們的輸入和輸出相對應

然後看到Regression model回歸模型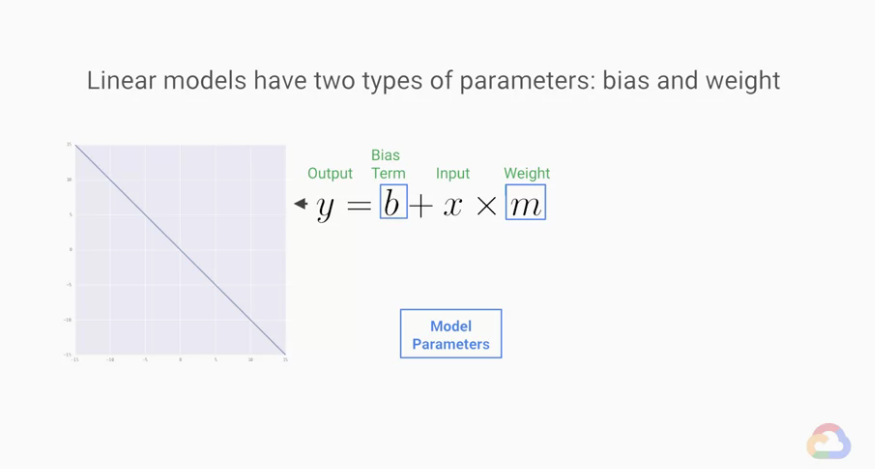

這是一個函數方程式y = b + x * m(廢話X)
y是我們的輸出，X是輸入，透過調整 b 和 m 讓輸入盡可能等於輸出
有了這個方程式，幾乎可以解決二為平面上大多數問題，
更多甚至到 n 維都可以由二維往上推

This same concept of a relationship defined by a fixed ratio change between labels and features can be extended to arbitrarily high dimensionality, both with respect to the inputs and the outputs. Meaning, we can build models that accept many more features as input, model multiple labels simultaneously, or both.

當增加 n 個輸入也就代表增加 n 個維度，同時為 n 個輸入或更多標籤建模
所以當增加輸入的維數時，我們的斜率項 m 就變成 n 維度 我們稱這個 m 為權重。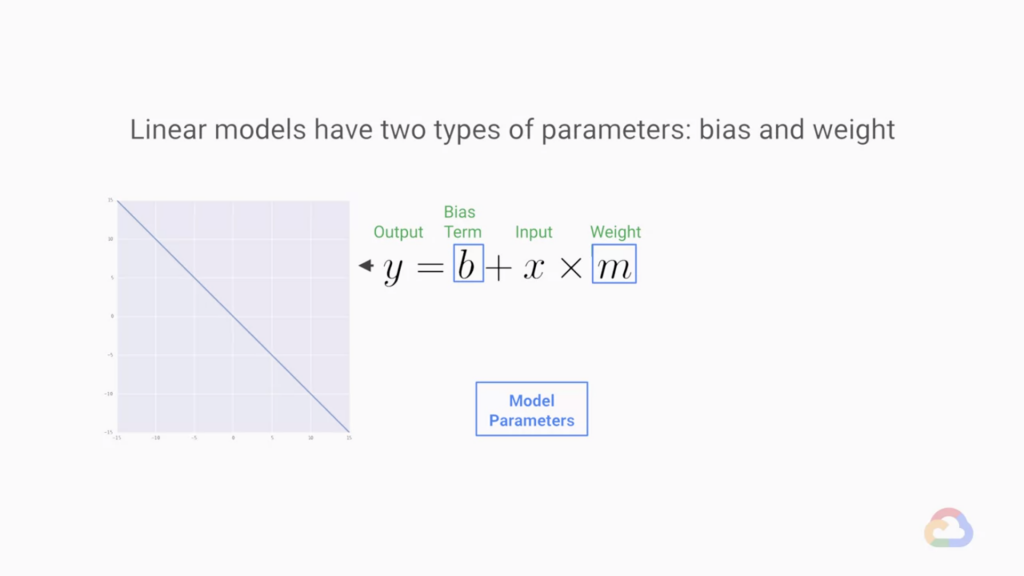

從二維變為 n 維的同時，原本的斜率 m 也變成了超平面 ω
實際上我們有輸入和輸出 x 和 y，配合 n 維度的解
只需要調整參數 b 和 ω使等式恆成立
是不是很簡單呢 oωo

參考資料

Google ML 課程
函數-維基百科

結語和一些小心得

感謝閱讀 今日里程數－2500字

如果圖片侵權通知我，我會將圖片刪除