梯度下降法

在上一篇文章當中，我們談到機器學習訓練優化的過程可視為一個不斷地尋找一組能最小化損失函數的模型參數的過程，但是卻尚未解釋我們是如何去尋找那組最適當之模型參數的? 儘管我們可以使用損失函數來判斷我們在目前優化階段上表現如何，但是有沒有一個方法來引導我們該往哪個方向以及調整多少? 今天即將和各位介紹的 梯度下降法(Gradient Descent) 就能夠幫助我們回答這個問題。

梯度下降法是一個在機器學習領域當中經常被使用的經典方法，其過程可以使用一個假想的登山例子來幫助想像。當一位登山者在攻頂途中，假設今天他的手上並沒有指引明確方向與路線的任何工具，他該如何達成目標呢? 這時他可以使用的方式為先判斷周遭的坡度為何，若其中有一個坡度為向上的路線(斜率為正值)，他將往該方向嘗試，在下一步時，他在延續此方法，首先判斷四周的坡度，接著再往坡度向上的方向繼續邁進，慢慢地，等到該登山者發現四周皆為平地時(斜率為零)，他就有非常大的可能是已經攀登至峰頂了(可視為最大值)。

而在機器學習的優化過程裡其實也是一個類似的過程(見圖1)，只是今天我們所面對的問題是要尋找損失函數的最小值，所以在調整模型參數的方向上，會變成是當前斜率的反方向(見圖2與圖3)。

而除了優化過程中前進的方向外，每次調整的大小也是相當重要的，若我們每次調整的步伐長度太小，我們將花上更長的時間才能讓優化過程收斂，而如果步伐長度太大時，則會導致調整幅度過大，會不斷地超過收斂的範圍，難以完成優化的過程(見圖4與圖5)，通常此步伐長度在機器學習當中是由一個被稱為 學習率(Learning Rate) 的 超參數(Hyperparameter) 所決定的。

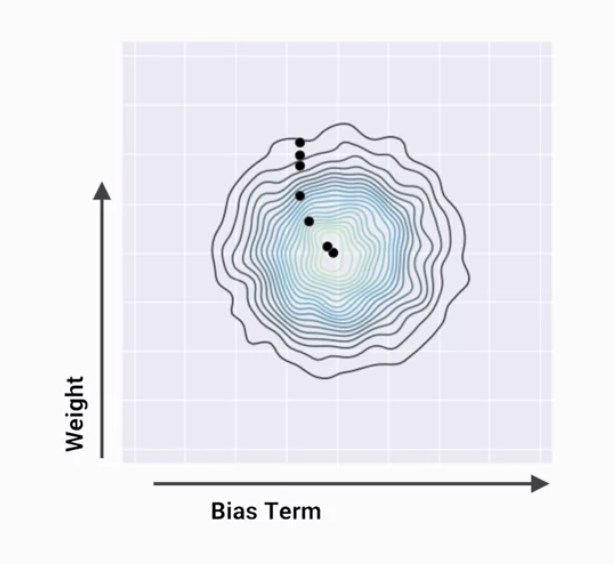
圖1
Source: Coursera - Launching into Machine Learning

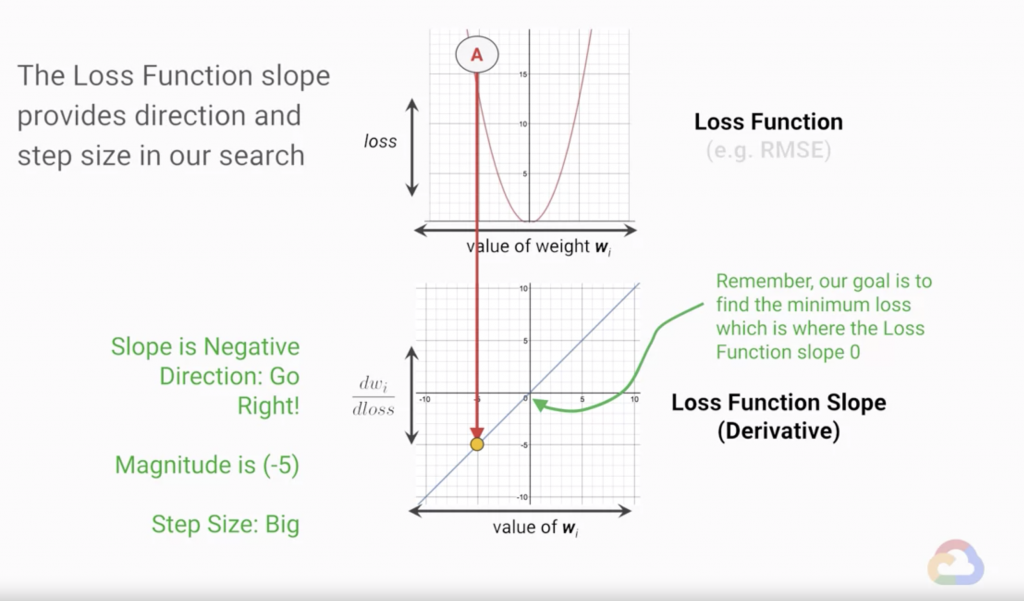
圖2
Source: Coursera - Launching into Machine Learning

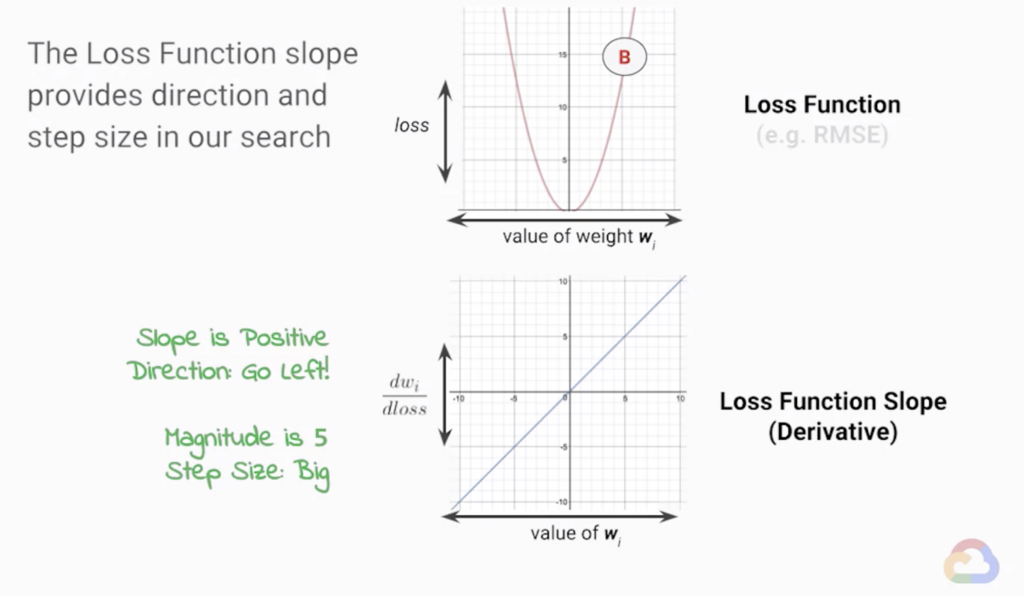
圖3
Source: Coursera - Launching into Machine Learning

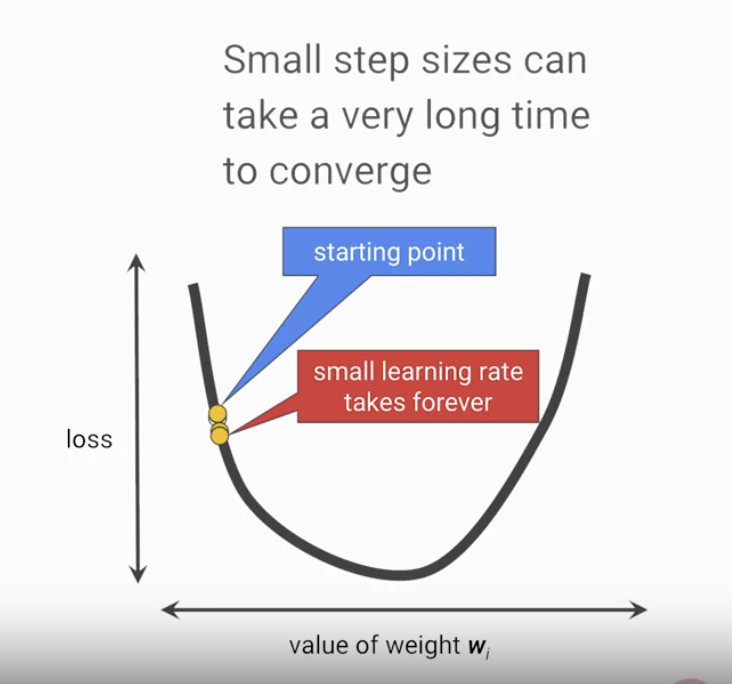
圖4
Source: Coursera - Launching into Machine Learning

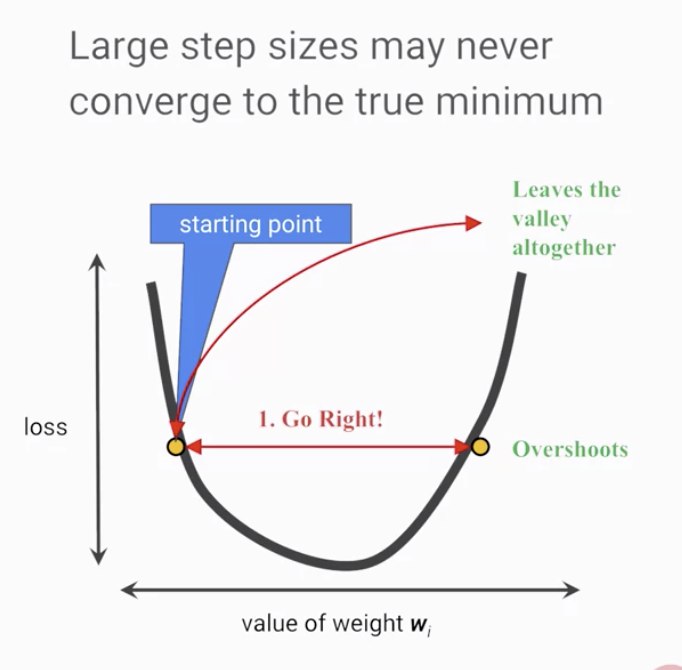
圖5
Source: Coursera - Launching into Machine Learning