損失函數

機器學習的訓練過程可以視為在選定的模型之下，針對所給定的資料集，尋找出一組最適合的 模型參數(Model Parameter) ，以達到最好的表現。而在尋找最終模型參數的階段，是一個不斷嘗試各種模型參數組合在訓練資料上的表現，並且不斷優化的過程，在這個優化的過程中，需要有個數值去衡量目前的表現如何，並且該往什麼方向繼續嘗試優化下去，而這個指導模型優化過程的數值就是我們今天要介紹的 損失函數(Loss Function) 。

從損失函數的名稱上來看，我們可以知道損失函數是模型在優化過程中必須去極力 最小化(Minimize) 的數值，並且根據所使用的模型，該損失函數也必須滿足一些條件才可以讓模型順利地使用，比如說可以進行微分等。選定適合的損失函數對於我們的模型訓練過程是相當重要的。以下我將會針對機器學習當中的兩種問題類型，也就是回歸與分類問題，分別去介紹裡面有哪些常見的損失函數。

首先是在回歸問題當中，常見的損失函數有 均方誤差(Mean Square Error, MSE) (註1)，用以衡量預測值和真實值之間誤差平方的平均值。另外還有針對均方誤差取平方根的 均方根誤差(Root Mean Square Error, RMSE) (見圖1與註2)，可以得到和目標值相同的單位。

而在分類問題當中，常見的損失函數為 交叉熵(Cross Entropy) (見圖2與註3)，考量對類別進行分類預測的機率與真實值，以大幅度地懲罰分類錯誤程度大的狀況，引導正確的優化方向。

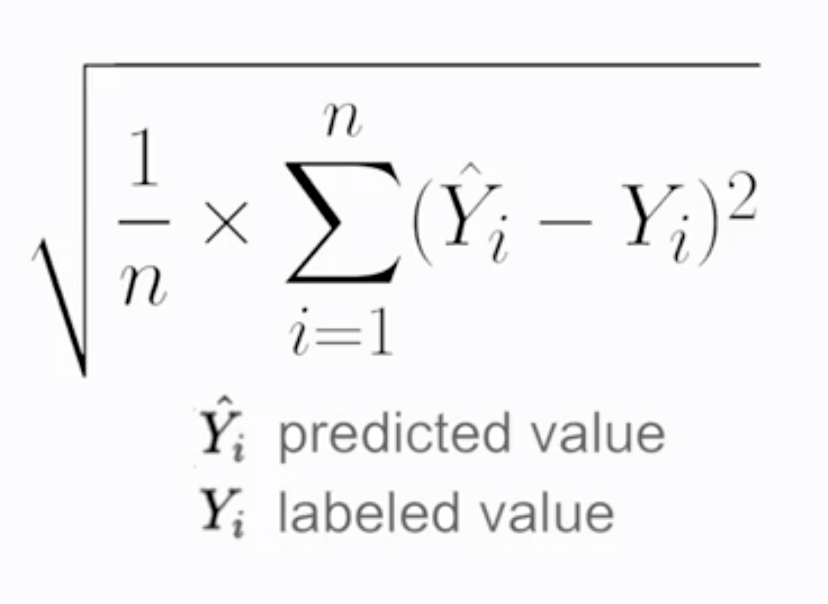
圖1
Source: Coursera - Launching into Machine Learning

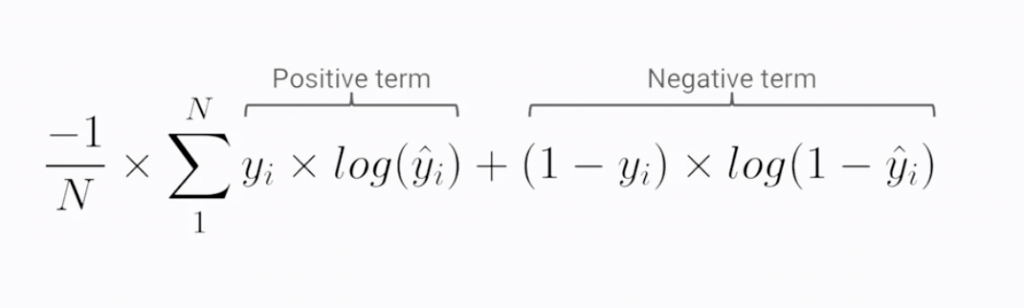
圖2
Source: Coursera - Launching into Machine Learning

註1: https://zh.wikipedia.org/wiki/%E5%9D%87%E6%96%B9%E8%AF%AF%E5%B7%AE
註2: https://zh.wikipedia.org/wiki/%E5%9D%87%E6%96%B9%E6%A0%B9%E8%AF%AF%E5%B7%AE
註3: https://zh.wikipedia.org/wiki/%E4%BA%A4%E5%8F%89%E7%86%B5