numpy 底層是 C 語言在計算所以非常快，通常會用在矩陣運算上．

安裝 numpy

pip3 install numpy

使用 numpy 建立一維矩陣

>>> import numpy as np
>>> np_array = np.array([1,2,3])
>>> print(np_array)
[1 2 3]

建立一維矩陣並設定元素的型態

>>> np_array = np.array([1,2,3] , dtype=np.float)
>>> print(np_array)
[1. 2. 3.]
>>> print(np_array.dtype)
float64

建立二維矩陣

>>> np_array = np.array([[1,2,3],[4,5,6]])
>>> type(np_array)
<class 'numpy.ndarray'>
>>> print(np_array)
[[1 2 3]
 [4 5 6]]

看矩陣的維度

>>> np_array.ndim
2

看矩陣的行列數

>>> np_array.shape
(2, 3)

看矩陣的元素

>>> np_array.size
6

建立初始值為 0 的 2 列 3 行的矩陣．

>>> np_array = np.zeros((2,3))
>>> print(np_array)
[[0. 0. 0.]
 [0. 0. 0.]]

建立初始值為 1 的 2 列 3 行的矩陣．

>>> np_array = np.ones((2,3))
>>> print(np_array)
[[1. 1. 1.]
 [1. 1. 1.]]

使用 linspace 建立一個從 1 到 10 之間分成 6 等分的數組．

>>> np_array = np.linspace(1,10,6)
>>> print(np_array)
[ 1.   2.8  4.6  6.4  8.2 10. ]

將上面的數組 reshape 成 2 列 3 行的矩陣．

>>> np_array = np.linspace(1,10,6).reshape((2,3))
>>> print(np_array)
[[ 1.   2.8  4.6]
 [ 6.4  8.2 10. ]]

2 個矩陣的計算

>>> a1 = np.array([1,2,3,4])
# 建立一個 [0 1 2 3] 的矩陣
>>> a2 = np.arange(4)
>>> print(a1)
[1 2 3 4]
>>> print(a2)
[0 1 2 3]
>>> print(a1 + a2)
[1 3 5 7]
>> print(a1 - a2)
[1 1 1 1]
>>> print(a1 * a2)
[ 0  2  6 12]

將 2 個矩陣相乘後做相加

>>> print(np.dot(a1,a2))
20

argmin 取出矩陣元素最小值的 index，argmax 取出矩陣元素最大值的 index．

>>> a = np.arange(2,14).reshape((3,4))
>>> print(a)
[[ 2  3  4  5]
 [ 6  7  8  9]
 [10 11 12 13]]
>>> np.argmin(a)
0
>>> np.argmax(a)
11

將元素作累加

>>> np.cumsum(a)
array([ 2,  5,  9, 14, 20, 27, 35, 44, 54, 65, 77, 90])

將元素作相減

>>> np.diff(a)
array([[1, 1, 1],
       [1, 1, 1],
       [1, 1, 1]])

Cosine similarity

餘弦相似度(Cosine similarity)的公式如下 :

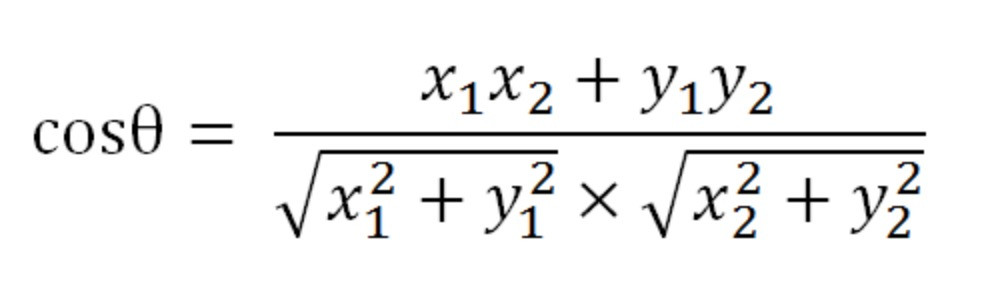
使用 numpy 來做就會是

>>> a1 = np.array([1, 2, 2, 1, 1, 1, 0])
>>> a2 = np.array([1, 2, 2, 1, 1, 2, 1])
>>> cos_sim = np.dot(a1,a2) / (np.linalg.norm(a1) * np.linalg.norm(a2))
>>> print(cos_sim)
0.9381941874331419

所以 a1 跟 a2 的餘弦相似度是 0.93 ，餘弦相似度的值越接近 1 表示兩個向量的夾角越小表示它們越接近也就越相似．