上一次談到『假設檢定』(Hypothesis Testing),它可以檢定一項實驗是否有顯著性的效果,但是,我們要蒐集多少樣本才能驗證實驗的可靠度呢? 這時就要借助『檢定力分析』(Power Analysis)來幫我們解決這個問題。
回顧一下假設檢定之混淆矩陣(Confusion Matrix),詳細的說明請參閱這一篇。
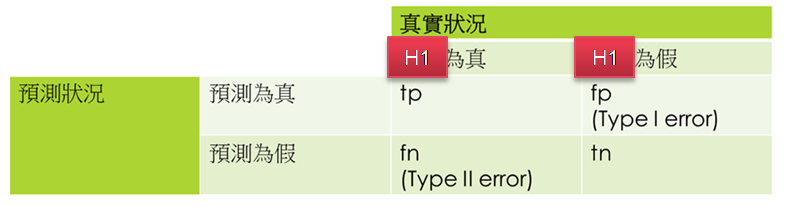
圖. 假設檢定之混淆矩陣(Confusion Matrix)
假設檢定是在避免『型一誤差』(Type I Error),即效果不顯著時(H0為真),我們卻誤認為實驗有效(H1為真),相對的,『型二誤差』(Type II Error)是當效果顯著時(H0為假),卻誤認為實驗無效(H1為假),檢定力分析希望避免此一錯誤,亦即當效果顯著時,我們有多少機率可以偵測到此一效果,因此,兩者是互補的分析方法。
『型二誤差』以β表示,檢定力(Power) 等於 1 - β。 例如Power = 0.2,就表示只有20%的機率,可以偵測到效果是顯著的,因此建議檢定力通常設為 0.8 或更高。
檢定力與樣本大小(n)、效應值(effect size)高度相關,三者在給定的臨界值(α)下,形成一等式的關係。
效應值(effect size)是指干預組和控制組之間差異量,其絕對值越大表示效應越強,也就是差異越明顯。因此,科學家 Cohen 定義下表說明效應值(Cohen's d)的效果:
| # | 效應值(d) | 意義 |
|---|---|---|
| 1. | 0 - 0.2 | 可忽視的 |
| 2. | 0.2 - 0.5 | 小 |
| 3. | 0.5 - 0.8 | 中 |
| 4. | 0.80 + | 大 |
效應值(d) = 0.2,表示希望干預組比控制組差異達20%,若效應值設的很小,表示我們希望能偵測到很小的差異,所以,需要的樣本數就要很大。
所以,進一步設定檢定力與效應值的水準,就可以知道我們要蒐集多少樣本才夠,計算很簡單,statsmodels 套件直接支援如下:
from statsmodels.stats.power import tt_ind_solve_power
# effect_size: 效應值
# nobs1: 樣本數,設為 None,表示要求算樣本數
# alpha:臨界值(α)
# power: 檢定力
# ratio: 干預組與控制組的樣本數比例,若不等於1,nobs1 算出來的是較少的樣本數,nobs2 = nobs1 * ratio
# alternative: 單尾或雙尾檢定,單尾再分右尾(larger)及左尾(smaller)
tt_ind_solve_power(effect_size=0.2, nobs1 = None, alpha=0.05, power=0.8, ratio=1, alternative='two-sided')
函數傳回的結果是每組需要蒐集的樣本數,若ratio不等於1,則另一組樣本數(nobs2) = nobs1 * ratio。
談到這裡,對於機器學習要蒐集多少樣本,準確率/精確率/召回率才具有公信力,構建了一個初步的概念,同時也是這一系列的文章告一段落了(江郎才盡)。
