前言

昨天我們用-greedy來當作我們的目標policy，並用同樣的policy來與環境互動，這樣跟我們的目標好像有點衝突，一邊要學習optimal policy；一邊又要保持-soft來進行exploration。

實際上，我們可以將目標policy與互動用的policy分開，幫助我們同時進行exploration與exploitation，稱為off-policy；而之前用同個policy同時當作目標policy與行為policy的方法就稱為on-policy

Importance Sampling

在進入off-polciy之前，必須先了解importance sampling的概念。我們將policy分成兩個，

• 與環境互動的policy稱為behavior policy，我們寫作
• 而我們要學習的optimal policy稱為target policy，我們寫作

如果我們用behavior policy來當作與環境互動的行為的話，求出來的期望值為，但我們想要知道的應該是才對。
透過importance sampling，我們可以某個分布中採樣，並用來估測另一個分布中的值。

簡單的推導可以看下圖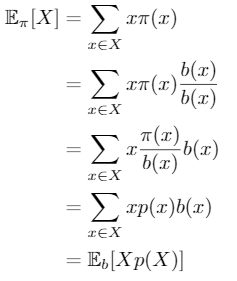

從取樣的期望值為從分布中取樣在乘上兩個分布的比例，被稱為importance ratio

上述公式可以擴展到的期望值，因為為時間到的累積reward，而每次reward的回傳也會因policy的不同而不同，所以我們的importance ratio必須考慮到時間到的轉移機率，寫作

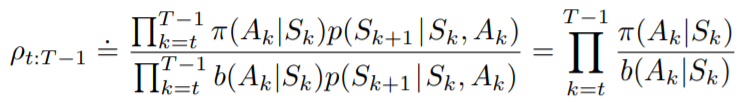
帶回剛剛推導的期望值公式，得到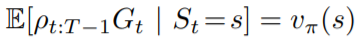

就能利用behavior policy來估測target policy的值囉！

Off-Policy Monte Carlo

昨天介紹的monte carlo稱為on-policy monte carlo，on-polciy方法的target policy與behavior policy相同，故稱為on-policy。

現在我們來實現off-policy版本的monte carlo
把target policy和behavior policy分開，一個為我們的目標policy，一個為與環境互動用的policy。

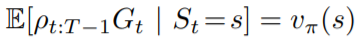
根據上面的公式，期望值可以跟on-policy monte carlo一樣用一般平均來算，但在這裡我們改用加權平均數來計算，表示為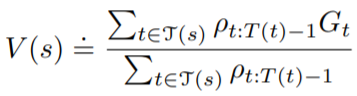

其中指的是在state 下的timestep集合

加權平均數的variance會比直接平均來的小，可以參考Sutton書中p105

另外，加權平均數也可以用incremental的方式來計算，可以參考裡的weighted mean部分，這邊就不做另外的推導。

將上面的內容寫成新的演算法如下：

其中

• epsiode是根據而不是來決定
• 的更新方式就是以incremental與weighted mean來實現
• 為importance ratio，跟一樣從epsiode的結尾往回計算比較方便
• 為到的和
• target policy是將greedy action的機率設為1的方式更新
• 因為是greedy action，所以當時，，造成，故後面都不需要更新，可以直接break

Blackjack

用新的off-policy monte carlo來看看結果跟昨天是否一樣

import gym
import numpy as np
import sys
from collections import defaultdict

env = gym.make('Blackjack-v0')

num_episodes = 500000
gamma = 1.0
epsilon = 0.2

returns_sum = defaultdict(float)
returns_count = defaultdict(float)
Q = defaultdict(lambda: np.zeros(env.action_space.n))
C = defaultdict(lambda: np.zeros(env.action_space.n))
behavior = defaultdict(lambda: np.ones(env.action_space.n) / env.action_space.n)
target = defaultdict(lambda: np.ones(env.action_space.n) / env.action_space.n)

for i in range(num_episodes):
    state = env.reset()
    episode = []
    while True:
        action = np.random.choice(np.arange(env.action_space.n), p = behavior[state])
        next_state, reward, done, info = env.step(action)
        episode.append((state, action, reward))
        if done:
            break
        state = next_state
    update(episode)
    #first_visit_update(episode)
    #every_visit_update(episode)
    print(f'\repisode: {i + 1}/{num_episodes}', end = '')
    sys.stdout.flush()

上面是與昨天的程式碼很像，把first_visit_update與every_visit_update改成off policy的update、增加C變數用來實現incremental的部分以及將原本policy改成behavior policy與target policy兩種

這邊實現的是every visit的off policy版本

def update(episode):
    G = 0
    W = 1
    for idx, (state, action, reward) in enumerate(episode[::-1]):
        G = gamma * G + reward
        C[state][action] += W
        Q[state][action] += (W / C[state][action]) * (G - Q[state][action])
        pi_S = np.argmax(Q[state])
        target[state] = np.zeros(env.action_space.n)
        target[state][pi_S] = 1
        if action != pi_S:
            break
        W = W * 1. / behavior[state][action]

update部分直接參考演算法實作

# evaluation
win = 0
for i in range(num_episodes):
    state = env.reset()
    while True:
        action = np.argmax(target[state])
        next_state, reward, done, info = env.step(action)
        if reward == 1:
            win += 1
        if done:
            break
        state = next_state
print(f'\nWin Rate: {win / num_episodes}')

最後用target policy評估勝率，跟on-policy一樣為43%左右。

總結

on-policy和off-policy的概念在之後的q learning與sarsa中也會看到，強化學習演算法的一種分類。
明天將會進到強化學習裡最有名的Temporal-Difference Learning(TD Learning)，將會用到之前教的所有概念，來實現簡單又快速的演算法，所以前面有不懂得趕快回去複習或發文喔！