前言

我們不一定會知道環境的Dynamic，昨天的Taxi環境gym好心提供給我們，但如果像是更複雜的環境，比如自駕車、21點、圍棋等等。如果要將所有機率算出來，再算Value Function就有點困難。

蒙地卡羅方法(Monte Carlo Method)

這時候蒙利卡羅方法就有用了，還記得大數法則(Law of large numbers)嗎？只要抽樣的樣本數越多，就越能趨近期望值。

而我們說過強化學習中的Value Function，其實就是求全部Reward和的期望值：

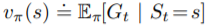
根據大數法則，我們可以知道當我們的樣本數越多，就離真實值越近。這種用隨機採樣來估測問題的隨機性的方法，就稱為蒙地卡羅方法。

所以我們只要跑足夠多的Epsiode，得到足夠多的，再將這些平均(取期望值)，就是的估計值。

為在時間點上的State的Value

演算法相當簡單，只要把所有Return平均當成期望值

• Monte Carlo有first-visite與every-visite的版本，差別只在同個epsiode裡同個state要不要全部計算。
• 圖片標題上的Prediction為Policy Evaluation的另一種稱呼

Exploration and Exploitation

Monte Carlo Method也遵循著GPI的流程

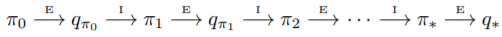
如果我們的Policy更新一直都是以更新的話，會造成我們的Agent停止探索更多的行為。
從例子上來看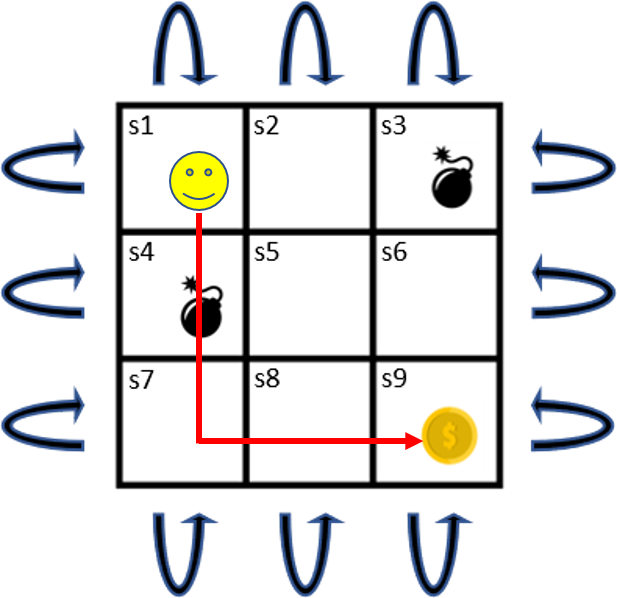

我們把每個State的Value Function都初始化為0，Agent在一開始為隨機策略，並在第一個episode走了塗上紅色的路線，獲得Reward = 5，假如為1，那根據上面的Monte Carlo Method，的Value Function都會變為5。Policy Improvement後的因為是根據greedy action，它會認為紅色這條路徑的Value比其他高，所以是最好的走法，導致之後的每一個episode都走同樣紅色的路線。其實不經過炸彈的Value會更高，但永遠都不會知道。

這種情況發生在用取樣方法的強化學習算法上，稱為Exploration and Exploitation trade-off。

• Exploration是指我們需要足夠的時間去探索未知的行為
• Exploitation是指我們利用已知的知識，來走最佳的行為

上面的情形是因為我們只花了一個episode去exploration，導致Agent的經驗不足，有很多方法可以在這兩種行為中平衡，這邊我們主要談論最簡單的-greedy。

-greedy

-greedy的概念非常簡單，我們的policy有的機率會做隨機行為，的機率做greedy action，這樣就能有的機率去做exploration來學習環境。
-greedy是一種-soft policy，-soft policy指的是對於所有State與Action，都滿足。
像是random policy也是一種-soft方法，普遍我們比較常用的還是-greedy。

Monte Carlo Control

上面提到Prediction指的就是Policy Evaluation的部分，用來估計目前的值，
而Control就是指Policy Improvement的部分，用來更新policy。

直接看演算法

1. 根據當前的跑完整個episode
2. 算每個時間點的
3. 將的值append到(s,a)的list中，方便計算平均
4. 將更新成的平均值
5. 依據-greedy更新

需要注意的是：

• 需要跑完整個episode才能得到
• 從算到比較方便
• 不用而用的原因是為了方便計算，不用特別去看下個State的Value
• 每次episode結束後更新一次policy，這邊policy看似很複雜的更新其實就是的機率為隨機，為greedy
• 這邊一樣是用first visit的方式，與every visit的方式差別不大，只要episode夠多都能夠收斂

Blackjack

今天我們使用gym裡blackjack環境

1. 不知道blackjack是甚麼的話可以看維基百科，簡單來講就是跟莊家比手牌中的大小，大的就獲勝，但手牌不能超過21點，而莊家在17點一下會持續抽牌
2. gym環境中的blackjack不包含特殊規則，且假設抽牌後牌會放回牌堆中，所以同樣一張牌可能出現不只一次

在blackjack中，只有兩種action：繼續抽牌、停止；三種reward：贏為+1，輸為-1，平手為0。
我們用Monte Carlo Method來找找看最佳的Value Function與Policy

import gym
import numpy as np
import sys
from collections import defaultdict

env = gym.make('Blackjack-v0')

num_episodes = 500000
gamma = 1.0
epsilon = 0.2

returns_sum = defaultdict(float)
returns_count = defaultdict(float)
Q = defaultdict(lambda: np.zeros(env.action_space.n))
policy = defaultdict(lambda: np.ones(env.action_space.n) / env.action_space.n)

先初始化需要的變數，這裡將returns、Q與policy都設為defaultdict，可以讓我們不用一開始就初始化state大小的array，有時候我們並不知道state總共有多少，或是state太多避免浪費空間。

def first_visit_update(episode):
    G = 0
    used = set()
    for idx, (state, action, reward) in enumerate(episode[::-1]):
        G = gamma * G + reward
        if (state, action) in used:
            continue
        returns_sum[(state, action)] += G
        returns_count[(state, action)] += 1
        Q[state][action] = returns_sum[(state, action)] / returns_count[(state, action)]
        A_star = np.argmax(Q[state])
        policy[state] = np.ones(env.action_space.n) * epsilon / env.action_space.n
        policy[state][np.argmax(Q[state])] += 1 - epsilon
        used.add((state, action))

定義first visit的update function，used用來判斷(state, action) pair是否visit過

def every_visit_update(episode):
    G = 0
    for idx, (state, action, reward) in enumerate(episode[::-1]):
        G = gamma * G + reward
        returns_sum[(state, action)] += G
        returns_count[(state, action)] += 1
        Q[state][action] = returns_sum[(state, action)] / returns_count[(state, action)]
        A_star = np.argmax(Q[state])
        policy[state] = np.ones(env.action_space.n) * epsilon / env.action_space.n
        policy[state][np.argmax(Q[state])] += 1 - epsilon

也可以用every visit的方法來更新Value

for i in range(num_episodes):
    state = env.reset()
    episode = []
    while True:
        action = np.random.choice(np.arange(env.action_space.n), p = policy[state])
        next_state, reward, done, info = env.step(action)
        episode.append((state, action, reward))
        if done:
            break
        state = next_state
    first_visit_update(episode)
    #every_visit_update(episode)
    print(f'\repisode: {i + 1}/{num_episodes}', end = '')
    sys.stdout.flush()

總共跑num_episodes次迴圈，每次迴圈先跟環境互動，並用一個list存放環境回傳的資訊。再用剛剛寫的update 更新Value

# evaluation
win = 0
for i in range(num_episodes):
    state = env.reset()
    while True:
        action = np.argmax(policy[state])
        next_state, reward, done, info = env.step(action)
        if reward == 1:
            win += 1
        if done:
            break
        state = next_state
print(f'\nWin Rate: {win / num_episodes}')

最後可以用求出的policy來看看我們的Agent效果好不好，記得這裡使用的是greedy action，我們不希望評估效能的時候還要繼續exploration。

最後勝率大約在43%左右，而隨機策略的勝率約為37%~38%，提升了5~6%

可以參考udacity裡的plot function來看我們的policy與value

from plot_utils import *

plot_policy(dict((k, np.argmax(v)) for k, v in Q.items()))
plot_blackjack_values(dict((k, np.max(v)) for k, v in Q.items()))

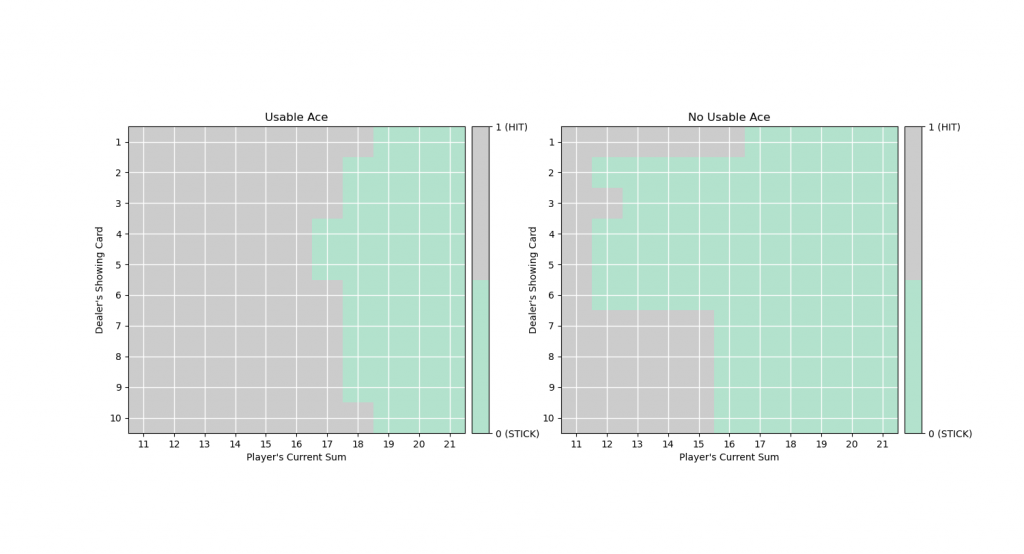
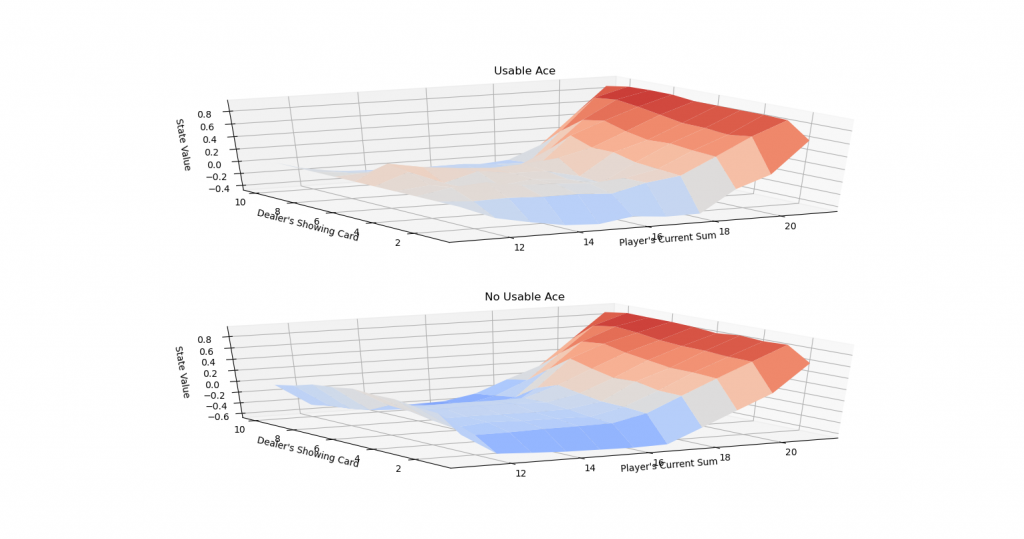
可以對照Sutton書中的optimal policy與對應的value：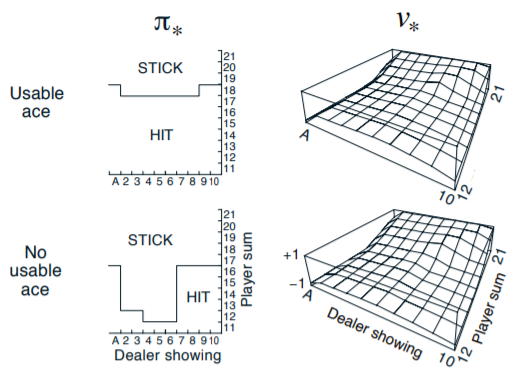

跟我們訓練出來得值差不多。

總結

Monte Carlo Method還有很多地方可以優化，像是

• 使用Epsilon Decay，會隨著時間越久，越來越少。可以在訓練後期越來越接近greedy policy。
• 使用Incremental Implementation，平均的部分可以改寫成incremental的形式，原本 的部分可以換成任意0~1的數，此數也被稱為Learning Rate

我們可不可以不要用-greedy來達到Exploration and Exploitation的平衡呢？只要行為的policy與目標的policy分開就行了，明天將會介紹這種方法。