機器學習的數學基礎不外乎就是離散數學或是線性代數(我沒學過這兩個科目，但我修過工程數學)。所以沒學過的朋友建議先去了解一下離散數學或是線性代數，才不會看到一堆數學式子時開始慌。所以這邊我就不細述矩陣及向量了。

從線性代數中可以知道，我們可以用多種方法來衡量事物。以下表為例，從表中大致可以分為兩類，成長期及成熟期。

• 成長期: 亞古獸、比丘獸
• 成熟期: 惡魔獸、奧加獸

因為成熟期數碼寶貝比較大隻，所以重量較重，因此利用重量就可以來判斷是成長期或成熟期。如果用數學來解釋的話，我們可以把每隻數碼寶貝當成是一個物件(這邊指每一個row)，物件包含很多的特徵(這邊指每一個column)，所以可以把這些物件看成是座標系統上的某一個點，透過計算點兩點之間的距離來衡量彼此的差異。

接下來我會介紹幾種計算距離的方式:

• Minkowski Distance
• Euclidean Distance
• Manhattan Distance
• Chebyshev Distance
• Cosine
• Hamming Distance
• Jaccard Similarity Coefficient

Minkowski Distance

它是一組距離的定義。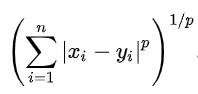

如上式所示，p是一個參數，p=1時，是Minkowski Distance。p=2時，是Euclidean Distance。p->∞時，是Chebyshev Distance。

Euclidean Distance

這個大家應該都不陌生，以前應該都有學過。沒錯，就是最常拿來計算距離的公式了，在歐式空間計算兩點的距離。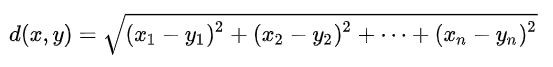

程式碼實作:

import numpy as np
v1 = np.mat([1,2,3])
v2 = np.mat([4,5,6])
print(np.sqrt((v1-v2)*(v1-v2).T))

Manhattan Distance

由下圖可知，Manhattan Distance為水平距離加垂直距離。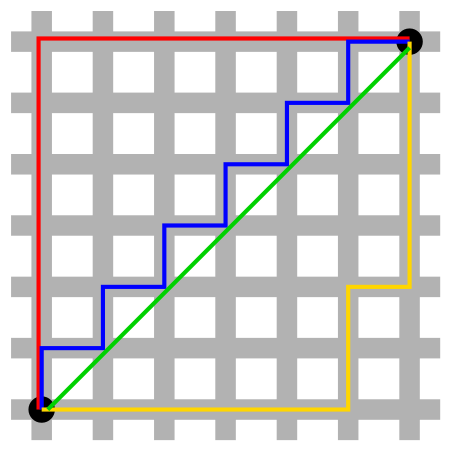

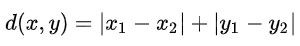
程式碼實作:

import numpy as np
v1 = np.mat([1,2,3])
v2 = np.mat([4,5,6])
print(np.sum(abs(v1-v2)))

Chebyshev Distance

Chebyshev Distance是指，西洋棋上王要從一個位子(x1, y1)移至另一個位子(x2, y2)需要走的步數，會發現步數為max(|x2-x1|,|y2-y1|)，所以d=max(|x2-x1|,|y2-y1|)。若是兩個n維向量(x11, x12,..., x1n)與(x21, x22,..., x2n)，d=max(|x1i-x2i|)，i從1到n。

程式碼實作:

import numpy as np
v1 = np.mat([1,2,3])
v2 = np.mat([4,5,6])
print(abs(v1-v2).max())

Cosine

數學中常常用Cosine來計算兩向量方向的差異，機器學習也常用此概念來計算兩向量的誤差。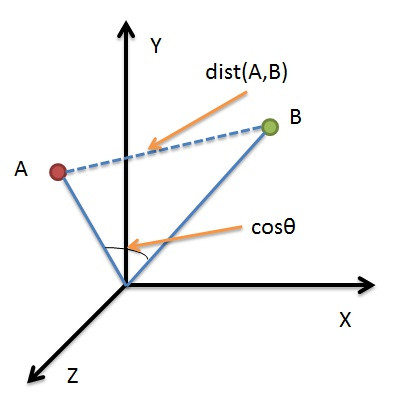

如上圖所示，Cosine值越大，代表兩向量間夾角越小；反之，Cosine值越小，代表兩向量間夾角越大。

程式碼實作:

import numpy as np
v1 = np.mat([1,2,3])
v2 = np.mat([4,5,6])
cosv = np.dot(v1, v2.T)/(np.linalg.norm(v1)*np.linalg.norm(v2))
print(cosv)

Hamming Distance

兩個長度相等的字串，將其中一個變換成另外一個字串所需要替換的字元個數。例如字串"1111"與"1000"之間的Hamming Distance為3。

程式碼實作:

import numpy as np
v = np.mat([[1,1,0,1,0,1,0,0,1], [0,1,1,0,0,0,1,1,1]])
smstr = np.nonzero(v[0] - v[1])
print(len(smstr[0]))

Jaccard Similarity Coefficient

用於比較樣本集的相似性與多樣性的統計量。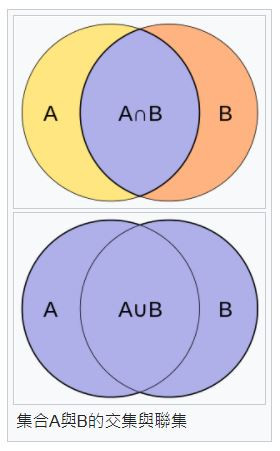

而Jaccard Distance，與Jaccard Similarity Coefficient是相反的概念。

程式碼實作:

import numpy as np
import scipy.spatial.distance as dist
v = np.mat([[1,1,0,1,0,1,0,0,1], [0,1,1,0,0,0,1,1,1]])
print(dist.pdist(v, 'jaccard'))