這是一個為了在實體機器上面互動而做的演算法，簡單來說是透過幾個理論去推演出來的
•兩個N維空間的向量，它們之間的距離可以定義為兩點之間的直線距離，稱為歐基里得距離（Euclidean Distance）

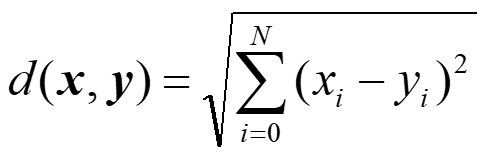
•假設有兩個3維空間的向量，分別為x(4 , 7)與y(7 , 11)，則此兩向量之間的距離為:

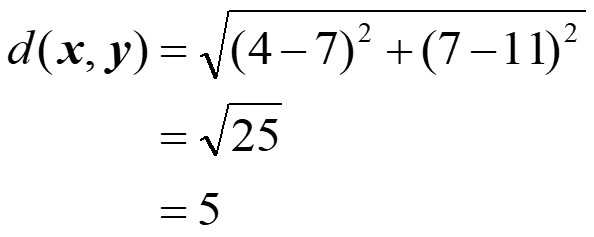
•若兩個向量的長度不同，那它們之間的距離，可利用動態時間校正來解決
•假設有兩個向量t(t1,t2,…,tN)與r(r1,r2,…,rM)，它們各別的長度為N與M，則DTW 的目標是要找出一條最短路徑，使得兩向量的距離最小

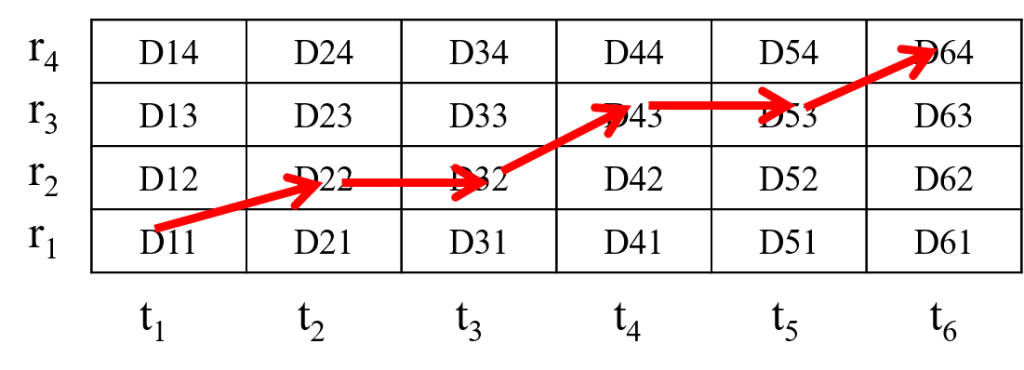
路徑必須滿足下列條件:
•端點關係：頭對頭、尾對尾
•局部關係：假設某一點D(i , j)為最佳路徑上的點，其前一點路徑只有三種可能 ： D(i-1 , j)、D(i-1 , j-1)和D(i , j-1)

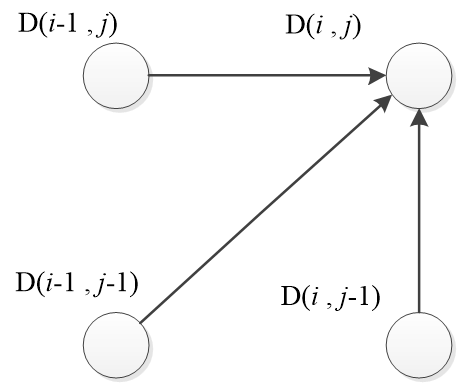
最後是DTW演算法的步驟 ：
•定義D(i , j)為ti與rj之間的距離值
•利用遞迴找出向量t與r之間的最小累積距離值A(N,M)，其遞迴關係如下所示:

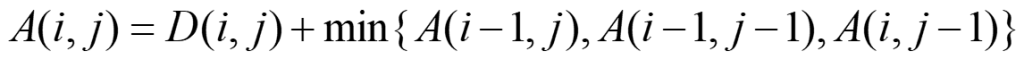
其中D(i , j)為ti與rj之間(i , j)的距離值 ， A(i , j)為原點(1 , 1)到(i , j)的最小累積距離值 。