75：...(ﾟдﾟ≡ﾟдﾟ)老師呢

75：老師抱歉我睡著了....(|||ﾟдﾟ)

RN：沒關係... 我習慣了...

75：那你...還願意繼續講嗎XD

RN：願意呀，哪次不願意 ( ˘•ω•˘ )
　　我們來說說以前在學校會學到的多項式函數的係數吧

上次說到如果我們要猜一個現象的函數
會先從低次的多項式函數開始做起
而這個多項式函數的係數會告訴我們那些事情呢

我們先從一次多項式函數
它的一次項係數告訴了我們這個函數的升降情形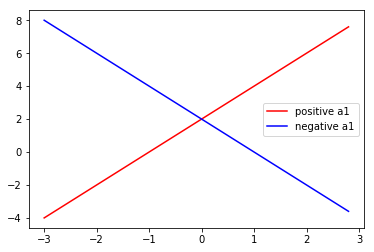

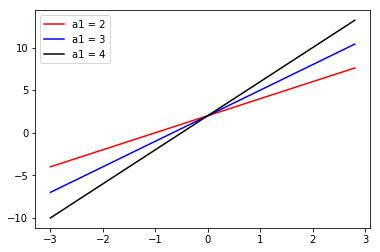
從上面兩張圖你可以看到

• 一次項係數為正：x 上升，則 y 上升；x 下降，則 y 下降
• 一次項係數為負：x 上升，則 y 下降；x 下降，則 y 上升
• 一次項係數的絕對值越大，則上升越快

一次項係數的解讀：
當 x 的值上升 1 時，對函數值的變化
它就如同幫你找到了一個趨勢
說明你的觀察中 x 與 y 的互動關係

murmur....(這也可以套用到一般的多變數多項式函式，只要這個多變數多項式函式的最高次項為 1)

75：蛤？你剛有什麼嗎？

RN：沒，我哪敢，你到現在還沒睡我就很開心了，哪敢再碎碎念呀~

為什麼會用到二次或更高次的多項式函數呢
就像我們之前有說過的
從二次多項式開始他可以「轉彎」

所以我們主要關注它轉彎的部分

那當然也是從最簡單的二次多項式開始
(你會發現數學很喜歡先簡化問題到最簡單的部分
解決後再往後推廣)

二次項係數告訴了我們轉彎的情形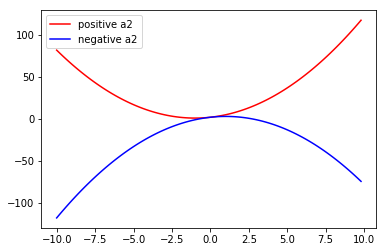

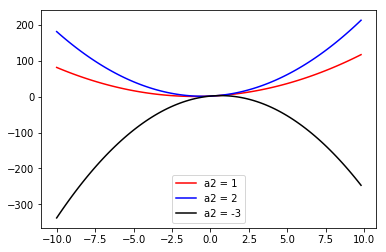
從上面兩張圖你可以看到

• 二次項係數為正：凹口向上，轉彎點是最小值
• 二次項係數為負：凹口向下，轉彎點是最大值
• 二次項係數的絕對值越大，則洞口越小(甩尾的那種)

二次項係數就如同幫你找到了一個規則
說明你的觀察中如果 x 往某個地方走，y 可以達到最大或最小
或是 y 的走勢有轉彎

murmur....(如果是一般的多變數多項式函式，就不是二次項係數而已，還要看 Hessian 矩陣)

75：(´～`)....我再想想好了

RN：沒關係，慢慢來，我先去吃水餃了~ 8~