因為曾經有的不好經驗，老頭和同事們對於避免過適有著「偏執狂式的執著」，這沒什麼不好，畢竟葛洛夫曾經說過「只有偏執狂才能生存 (Only the Paranoid Survive.)」（註一）。不過看了「Deep Double Descent」這篇論文之後才驚覺到，我們對於過適的了解可能太狹隘了。

在學習過適現象時，我們常常看到類似下面這張圖的說明：

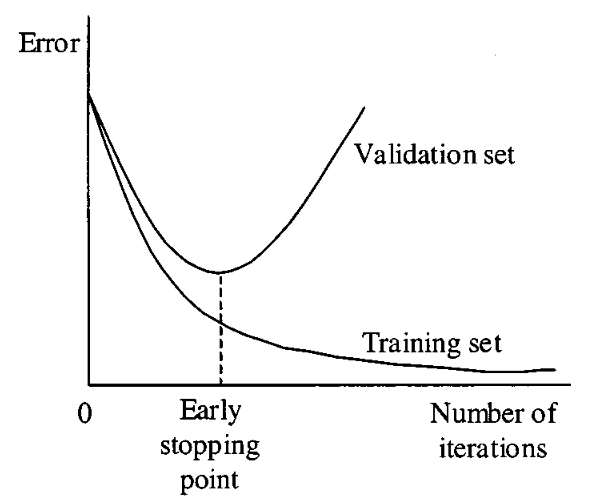
它告訴我們，過了「Early stopping point」之後，如果繼續訓練下去，儘管「Training set」的錯誤會逐漸減少，但「Validation set」的錯誤會越來越大，而整個模型就會過適。所以，為了避免過適，在模型訓練的過程中，我們要時時監測 Validation set 的錯誤率，當發現它開始提升的時候，就該停止訓練程序了。這個原則被大多數 AI 人視為金科玉律，而我們都沒有想過，如果我們一直把模型訓練下去，Validation set 的錯誤率會有怎樣的變化？「Deep Double Descent」這篇論文給了我們一些答案。

這篇論文全名為「Deep Double Descent: Where Bigger Models And More Data Hurt」（註二），它發現了在訓練 DNN 的過程中一個所謂「Double Descent」現象，在論文的第 6 節，特別說明了訓練過程中的 Double Descent ，它的結論是：

過去我們認為模型訓練的過程分為兩個階段，第一階段時，訓練資料和驗證資料的錯誤率的趨勢是一致的，兩者之間的差距有限；第二階段時，模型開始過適，驗證資料的錯誤率開始上升。然而我們的實驗結果卻顯示，並不是所有模型的訓練過程都只有這兩個階段，有時候，驗證資料的錯誤率在上升之後會再度下降，甚至於會下降到先前未曾到達的新低點！

下面這張圖就可以很明顯的看出 Double Descent 現象（現在大家應該可以了解為什麼作者稱之為 Double Descent，因為有兩段下降的區段！）

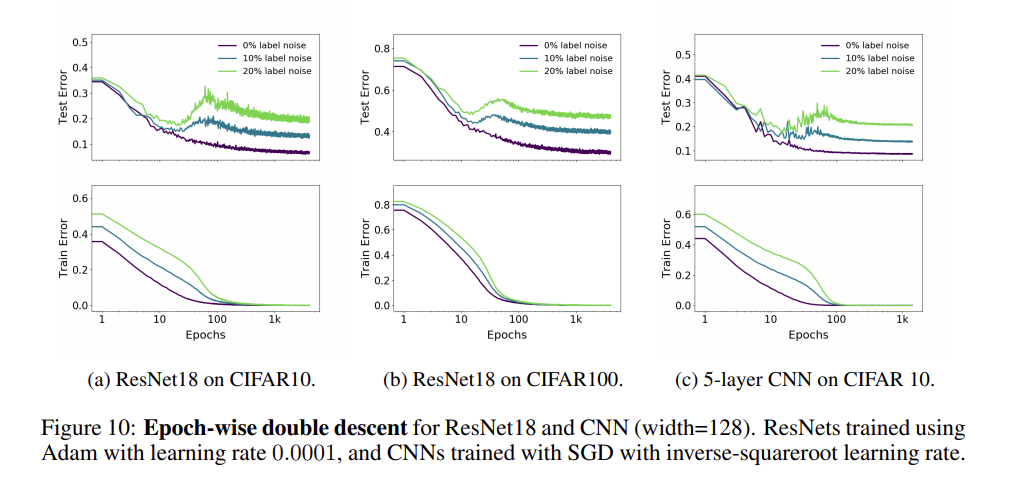
因此，老頭和同仁們修正了我們過去的 S.O.P.，如今，在訓練及調整模型的初期，我們仍然使用先前嚴格的避免過適流程，但在模型調整的最後階段，我們會在模型第一次發生過適時，記錄目前的 epoch 數（假設是 N)，讓訓練繼續下去，一直到 2N 個 epoch 為止。

有時候，真的有意外的驚喜！

（註一：安迪·葛洛夫（Andy Grove）英特爾創辦人之一，此語出自葛洛夫的著作 Only the Paranoid Survive，中文版譯名《10倍速時代》）

（註二：論文 arXiv 號碼 1912.02292 https://arxiv.org/abs/1912.02292 ）