上篇介紹了相關與相關係數，討論了誤把相關當因果的嚴重性。
這篇要再延伸介紹迴歸，然後解說一下機器學習的基本概念，
以及為什麼我說機器學習裡面充滿把相關當因果的問題。

在討論相關的時候，基本上我們是沒有方向性的。
也就是A跟B有關，並不能直接說是A造成B或是B造成A
(前面有討論過有相關性的兩個變數之間有可能的關係）
我們能從相關知道的事情是，
這兩個變數的值在其中一個往一個方向改變時，
另一個變數大概會往同個方向或反方向改變多少。

比如說，我們假設一個人看政治新聞的數量，
會跟他臉書所跟隨的政治人物的數量成正比（假設等比例），
我們就可以說，假設如果一個人看政治新聞的數量是A，
臉書所跟隨的政治人物數量是B，
那如果有另一個人他看政治新聞的數量是2A，
那我們就可以推測他跟隨的政治人物數量大概會是2B。

假設有另一個變數是信用卡欠款的機率(Y)，
他跟收入(X1)還有年紀(X2)都有關係，
那我們就可以找出Y跟X1還有X2的關係，
接著我們如果知道一個人的X1跟X2，
就可以大致推出Y是多少。

這就是「迴歸」的基本想法。

迴歸的想法就是，我們可以從一堆資料點中，
找出一條線去近似所有X（X1, X2, X3...)跟Y之間的關係，
就像這個圖：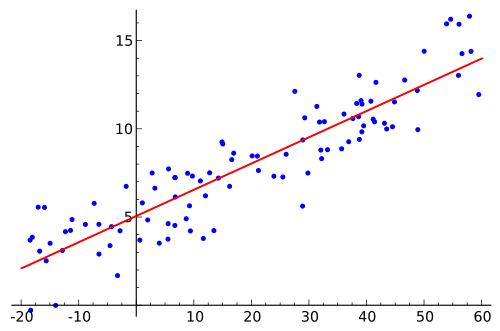

（圖片來源：https://commons.wikimedia.org/wiki/File:Linear_regression.svg）

藍色的是資料點，橫軸是X，縱軸是Y，
紅色的那條就是「迴歸直線」，也可以叫做「趨勢線」，
當我們有新的資料點且知道X是什麼的時候，
我們就可以從這條直線去推測Y值是什麼。

迴歸直線的算法是「最小平方差」，
也就是所有資料點與這條線的Y軸距離的平方和，
是所有可能的直線之中最小的。

這個例子是單一變數的迴歸，
如果我們有多個X變數，那麼這個概念就是往上推廣，
到迴歸平面，迴歸超平面，
總之就是在該維度中讓所有的點距離這個迴歸線/平面最近。
要注意的是迴歸中，所有的X必須要是獨立的，
不能有相依性，不然會造成相對應的變動量被加成的問題。

迴歸分析也可以被拿來當作推論統計檢定的方法，
而ANOVA其實也是迴歸分析檢定的一種特殊情況。
不過這部分不是我接下來想講的重點。

然後這上面舉的例子都是線性迴歸，
實際上迴歸線/平面也可以是曲線/曲面，
也就是所謂的非線性迴歸。
但這部分太過複雜，有興趣的人可以參考這篇。

那機器學習跟迴歸的關係是什麼呢？

首先我們先來定義一下「模型」這個概念。

「模型」是什麼呢？在統計或是在數學中，
模型是指一種數學表達，用來近似地描述特定對象。
有了模型之後，我們就可以基於模型，
來對原本的對象進行推測/更多的理解。
而模型的好壞，
也會影響我們能夠做出的推測和獲得的理解的品質。

就像一個火車模型，
非常普通的就只是大致模仿一台火車的外型，
但很厲害的就可以模仿火車在鐵道上的移動。
而非常差的長得可能根本就不像火車。

一個數學模型也是，
一個好的數學模型可以用來捕捉目標對象的性質，
甚至用來預測目標對象的可能行為。
但一個不好的數學模型，
就是一個與現實世界差距甚遠的產物，
做出來的推斷也沒有什麼意義。

機器學習，他的本質上就是從資料之中，
透過演算法去推出一個模型。
更精確的說，
機器學習的本質是由創建者建立一個模型的架構，
再透過演算法去從現有資料中推出架構中的細節。

就像上面的迴歸直線，
我們是先假設了我們要的是一條直線，
才去用方法算出那條直線應該長怎麼樣子。

下一篇我們再來細談機器學習如何使用模型做判斷，
而這之中有什麼問題吧！