前言

首先，先來介紹最常見的排序法，顧名思義就是將數字由大到小重新排列

生活常識

身為東方人，最喜歡作的動作大概就是比較了吧XD，跟兄弟姊妹比，跟同學比，甚至連鄰居也難逃被拿去比較，那要比什麼呢？無非是成績啦，或是身高、體重也會加入評比範圍，想必大家都有經歷過這個過程吧

圖片來源：https://www.pexels.com/zh-tw/photo/4412924/

以前安排學校的班級座位時，都會請同學們依照身高排列好，一直覺得這個過程很殘酷，因為很容易知道誰是班上最高，但同時，也會知道班上誰最矮XD

專業知識 - 排序 Sort

排序的是一種很常見的行為，主要是將資料由小到大、或由大到小排列，根據資料量的多寡又分為：

• 內部排序：資料量小，可在記憶體內完成排序
• 外部排序：資料量大，需透過硬碟才能完成排序

而相關的排序演算法有非常多種，其優點缺點與執行速度的快慢表現如何，會在這幾天逐一介紹

• 初等排序

1. 氣泡排序法 Bubble Sort
2. 選擇排序法 Selection Sort
3. 插入排序法 Insertion Sort
4. 謝耳排序法 Shell Sort)

• 高等排序

1. 快速排序法 Quick Sort
2. 合併排序法 Merge Sort
3. 堆積排序法 Heap Sort

專業知識 - 氣泡排序 Bubble Sort

又稱交換排序法，顧名思故就是與相鄰的資料兩兩比較，如果數字較大者在前面，則需交換位置到後面，這樣一來可確保，數字最大者會排在最後面

例子

假設目前有 5 個數字，排列情況由大到小為：9, 8, 7, 6, 5 以氣泡排序將排列改為由小到大

第一次掃描 9, 8, 7, 6, 5
1.　9 與 8 相比，發現 9 比 8 大，所以交換位置，排列狀況為： 8, 9, 7, 6, 5
2.　9 與 7 相比，發現 9 比 7 大，所以交換位置，排列狀況為： 8, 7, 9, 6, 5
3.　9 與 6 相比，發現 9 比 6 大，所以交換位置，排列狀況為： 8, 7, 6, 9, 5
4.　9 與 5 相比，發現 9 比 5 大，所以交換位置，排列狀況為： 8, 7, 6, 5, 9 (最大的 9 在最後面)

第二次掃描 8, 7, 6, 5, 9
1.　8 與 7 相比，發現 8 比 7 大，所以交換位置，排列狀況為： 7, 8, 6, 5, 9
2.　8 與 6 相比，發現 8 比 6 大，所以交換位置，排列狀況為： 7, 6, 8, 5, 9
3.　8 與 5 相比，發現 8 比 5 大，所以交換位置，排列狀況為： 7, 6, 5, 8, 9

第三次掃描 7, 6, 5, 8, 9
1.　7 與 6 相比，發現 7 比 6 大，所以交換位置，排列狀況為： 6, 7, 5, 8, 9
2.　7 與 5 相比，發現 7 比 5 大，所以交換位置，排列狀況為： 6, 5, 7, 8, 9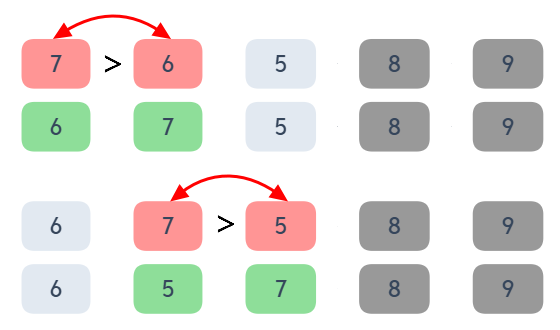

第四次掃描 6, 5, 7, 8, 9
1.　6 與 5 相比，發現 6 比 5 大，所以交換位置，排列狀況為： 5, 6, 7, 8, 9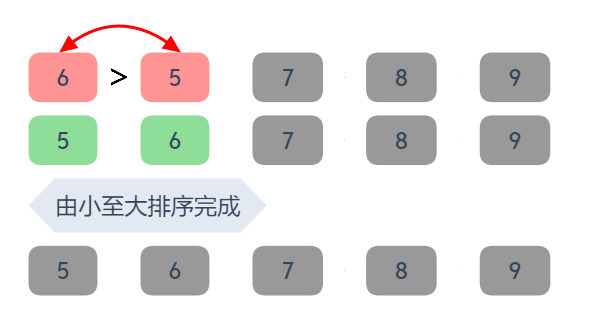

兩兩相比較，都沒有發生交換的動作時，就代表資料已由小至大排列完成

分析

• 最壞的情況
  資料是反序排序，如上述例子
  第一次掃描做了 4 次交換 = (5-1)次 = (n-1)次，n = 數字個數
  第二次掃描做了 3 次交換 = (5-2)次 = (n-2)次
  第三次掃描做了 2 次交換 = (5-3)次 = (n-3)次
  第四次掃描做了 1 次交換 = (5-4)次 = (n-4)次
  總次數為 = (n-1) + (n-2) + ... + 2 + 1 = ，取最高項次

• 最好的情況
  資料原先就已經排列好，則只需做 n-1 次的比較，發現沒有交換情況，時間為 O(n)

專業知識 - 選擇排序 Selection Sort

選擇排序重點在於選，此演算法會直接挑選出全部數值中的最小值出來做比較，若大小相反則交換，不會進行兩兩相鄰的比較

例子

假設目前有 5 個數字，排列情況由大到小為：9, 8, 6, 5, 7 以選擇排序將排列改為由小到大

• 第一個步驟 9, 8, 6, 5, 7
  鎖定第 1 個位置，在 8 6 5 7，4 個數字中選擇最小值，選到 5
  5 比 9 小，將 5 與 第 1 個位置的 9 交換，得到 5, 8, 6, 9, 7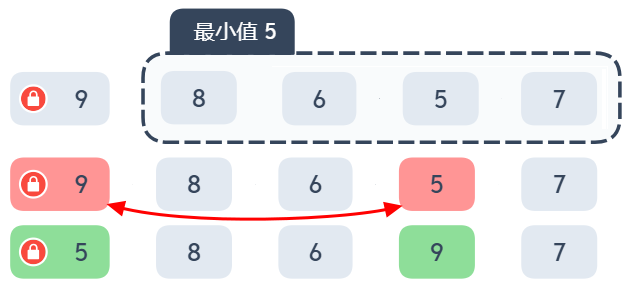
  

• 第二個步驟 5, 8, 6, 9, 7
  鎖定第 2 個位置，在 6 9 7，3 個數字中選擇最小值，選到 6
  6 比 8 小，將 6 與 第 2 個位置的 8 交換，得到 5, 6, 8, 9, 7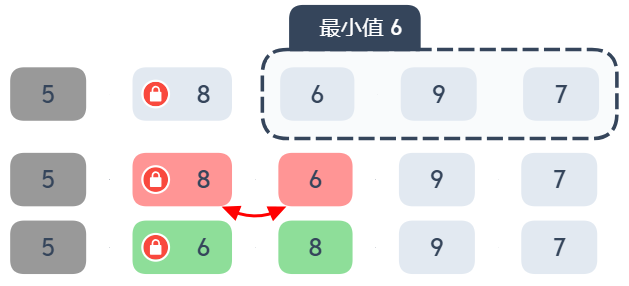
  

• 第三個步驟 5, 6, 8, 9, 7
  鎖定第 3 個位置，在 9 7，2 個數字中選擇最小值，選到 7
  7 比 8 小，將 7 與 第 3 個位置的 8 交換，得到 5, 6, 7, 9, 8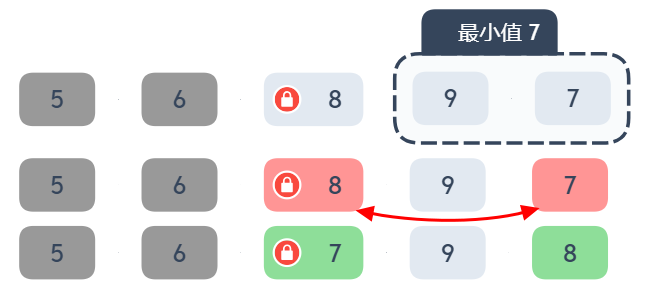
  

• 第四個步驟 5, 6, 7, 9, 8
  鎖定第 4 個位置，在 8，1 個數字中選擇最小值，選到 8
  8 比 9 小，將 8 與 第 4 個位置的 9 交換，得到 5, 6, 7, 8, 9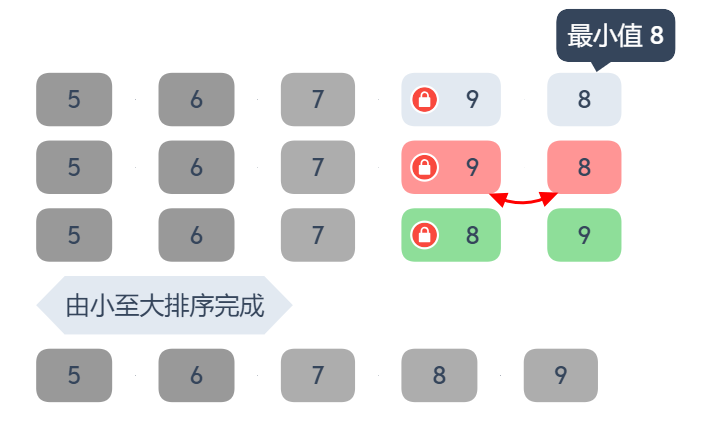
  

分析

• 最壞的情況
  第 1 個位置要與 4 個數中找到最小值 = 找(5-1)次 = (n-1)次，n = 數字個數
  第 2 個位置要與 3 個數中找到最小值 = 找(5-2)次 = (n-2)次
  第 3 個位置要與 2 個數中找到最小值 = 找(5-3)次 = (n-3)次
  第 4 個位置要與 1 個數中找到最小值 = 找(5-4)次 = (n-4)次
  找最小值的總次數為 = (n-1) + (n-2) + ... + 2 + 1 = ，取最高項次

• 最好的情況
  與最壞情況相同

今日小結

氣泡與選擇排序法算式很經典的排序演算法，在書籍中常常看到它們的介紹，也非常簡易好懂，明天再來介紹插入與合併演算法

今日謎題

最近的國慶日有一場音樂演奏會，聽說會出現某種樂器
你能由小至大排序以下數字 15, 3, 12, 5, 12，並根據下表推算出是哪一種樂器嗎？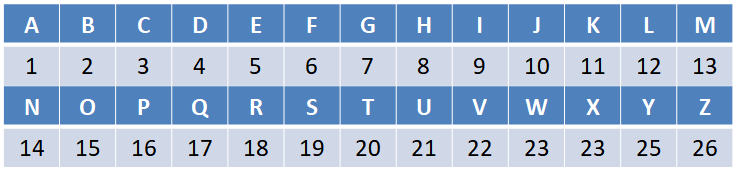

昨日解謎

謎題說明：根據圖片下方，有寫 FIND CODE，這邊可能會誤以為是要找程式碼，但其實不是，真正要找的是 C、O、D 與 E 在表格內的分佈，並把它們相連起來，即可得到 ALGO(演算法的縮寫)