前言

今天這兩個例子剛好可以用撲克牌舉例，也許會幫助你加深印象哦，一起來看看吧！

生活常識

你有玩過撲克牌嗎？通常拿到牌之後會需要根據牌的點數大小去做排序，你都是怎麼整理手牌的呢？像我自己的習慣是，先拿一張左邊的牌，然後看看右邊剩下的牌，再決定要將這張牌插入到哪個地方，不斷的拿最左邊的牌，掃描數字大小再選擇適當的地方插入，或是遊戲過程中再拿到新的牌，也會將新的牌插入到目前的已排序好的手牌當中

圖片來源:https://www.pexels.com/zh-tw/photo/800767/

另外在遊戲過程中，你有觀察過撲克牌的發牌方式嗎？其實沒有一定的發牌規則，只要玩家之間同意即可，但通常會以順時鐘或逆時鐘，逐一輪流發一張牌給玩家，直到發完為止，例如共有 12 張牌，玩家有 A、B、C、D 四位，所以可各拿 3 張，那在一疊牌中，他們各自會分配到牌堆中的第幾張如下表，所以 4 個玩家就有 4 份手牌，下表是玩家拿到的手牌，拿到牌之後就可以自行排序手上的撲克牌

玩家 | 大家拿到的第一張 | 大家拿到的第二張 | 大家拿到的第三張
------------- | -------------
A | 第 1 張 | 第 5 (1+4) 張 | 第 9 (5+4) 張
B | 第 2 張 | 第 6 張 | 第 10 張
C | 第 3 張 | 第 7 張 | 第 11 張
D | 第 4 張 | 第 8 張 | 第 12 張

圖片來源:https://www.pexels.com/zh-tw/photo/3279691/

專業知識 - 插入排序 Insertion Sort

當資料已經排序好，但又想新增資料時，就可以使用插入排序法，所以會有兩項資料

1. 已排序好的資料(例如已經牌好的手牌)
2. 想要新增的資料(新抽到的牌)

將想要新增的資料，逐一與排序好的資料做比對，即可找到合適的插入位置，是不是很像玩撲克牌整理手牌的過程

例子

欲將 9, 8, 6, 5, 7 由小至大排序

1. 讀取第一個數字 9 將它加入已排序好的資料中
2. 讀取第二個數字 8，加入排序資料之前，要先跟排序好的資料 9 比較，如果比 9 小，則放在 9 的前面
3. 讀取第三個數字 6，跟 8 9 比較，比 8 小，則 6 要放在 8 的前面
4. 讀取第四個數字 5，跟 6 8 9 比較，比 6 小，則 5 要放在 6 的前面
5. 讀取第五個數字 7，跟 5 6 8 9 比較，比 6 小，則 7 要放在 8 的前面
   最後會得到 5 6 7 8 9

分析

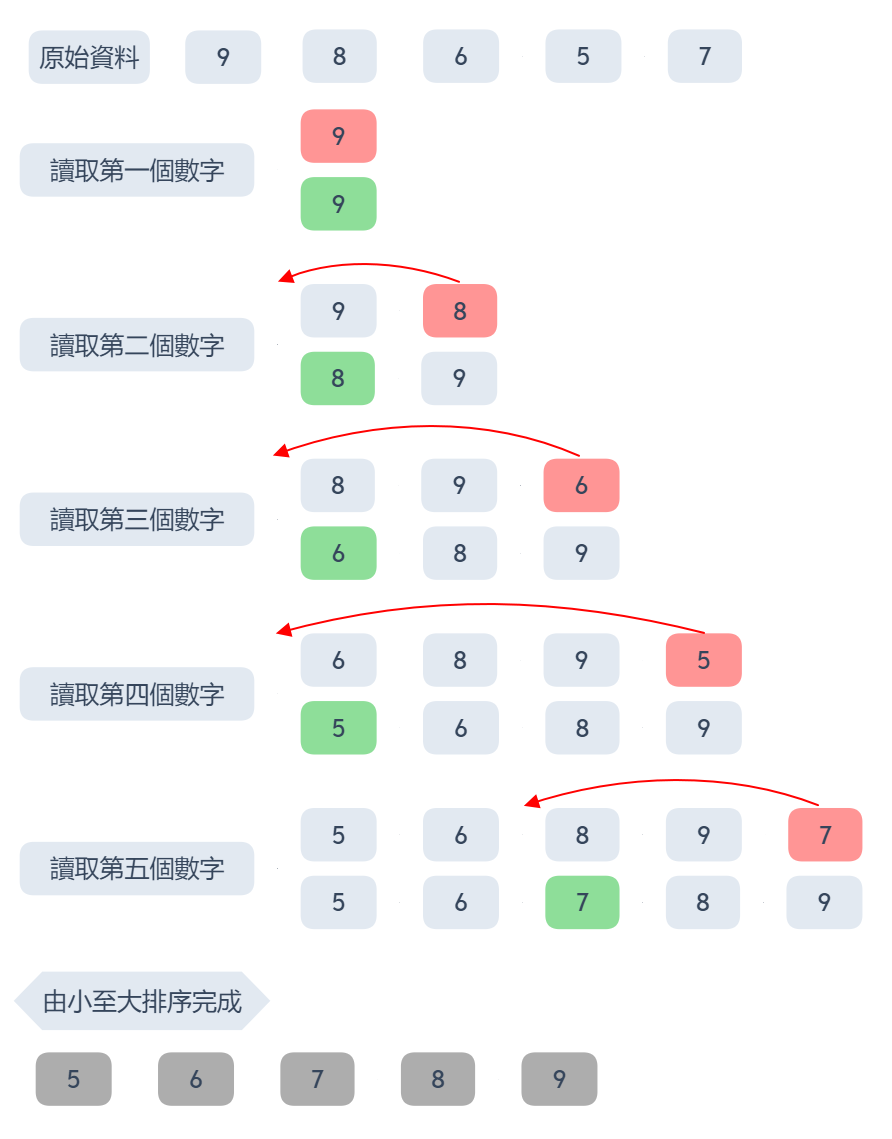
• 最壞的情況
  讀取第二個數字要與 1 個數相比 = 比 1 次 = (n-4)次，n = 數字個數
  讀取第三個數字要與 2 個數相比 = 比 2 次 = (n-3)次
  讀取第四個數字要與 3 個數相比 = 比 3 次 = (n-2)次
  讀取第五個數字要與 4 個數相比 = 比 4 次 = (n-1)次
  找最小值的總次數為 = (n-1) + (n-2) + ... + 2 + 1 = ，取最高項次

• 最好的情況
  O(n)，如果資料已經照順序排序好，則只需花 n-1 次的比較

專業知識 - 謝耳排序 Shell Sort

謝耳排序原理有點像插入排序，為插入排序的改良，可減少資料搬移的次數，其中會將資料分成多個小區塊，通常使用公式來決定要切幾個區塊，這邊的區塊會類似上述生活例子中的發牌方式，總共要發給幾位玩家，他們拿到牌之後，可以自行整理手上的卡牌，依照順序牌好

公式 1 ：

例如：今天有 8 個數字要排列， n = 8，可自行決定要除以 2 的幾次方，取整數或取上限值皆可

• 8 / 2 = 4 可切成 4 個區塊
  例如： 8 張牌，要分給 4 位玩家，每個人會拿到 2張牌，像是玩家 A 可針對拿到的第 1 張與第 5 張進行排序

玩家 | 第一張 | 第二張
------------- | -------------
A | 第 1 張 | 第 5(1+4) 張
B | 第 2 張 | 第 6 張
C | 第 3 張 | 第 7 張
D | 第 4 張 | 第 8 張

公式 2 :

而套用公式所計算出來的值可以稱為區間(Gap)或跨度(Span)，要注意的是，排序的最後一個步驟的區間一定要是 1

例子

欲將 20, 25, 45, 3, 8, 5, 6, 9 由小至大排序，首先要先決定要使用何種公式來切割區塊

• 步驟一
  區間值 = 4，使用公式：，8 / 4 = 2，可區分成 2 個區塊，每個區塊含有 4 個數字，再重新幫區塊內的數字給予新的編號，並將相同編號的數字重新排列，例如 20 與 8 的編號都是 1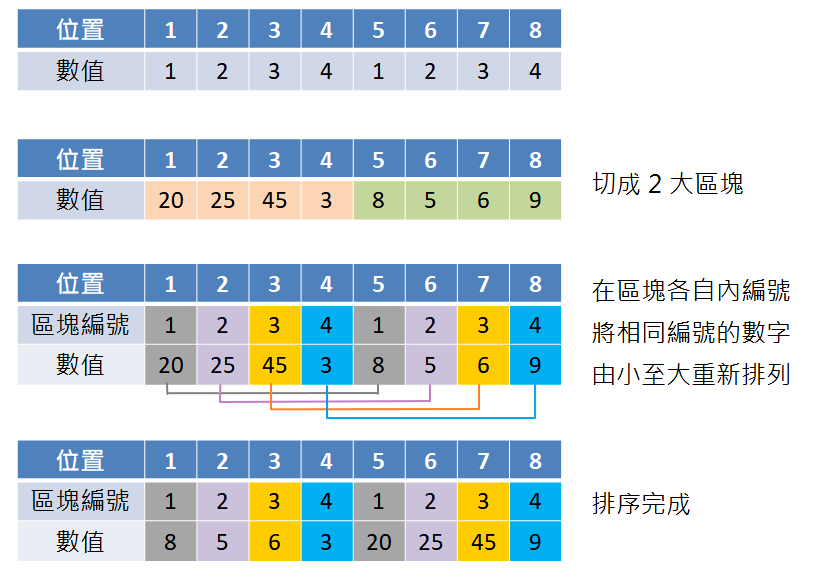

• 步驟二
  區間值 = 2，可區分成 4 個區塊，每個區塊含有 2 個數字，再重新幫區塊內的數字給予新的編號，並將相同編號的數字重新排列，例如 5, 3, 25 與 9 的編號都是 2，則互相比較大小，小的數字往前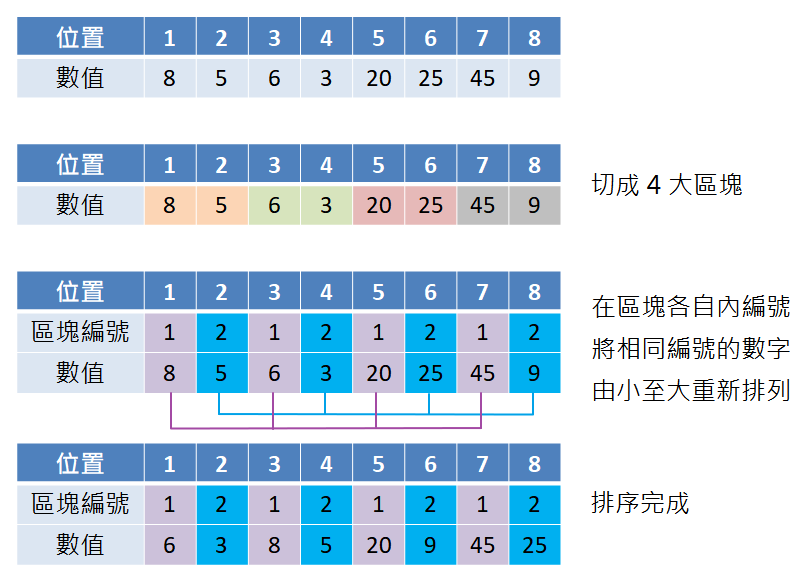

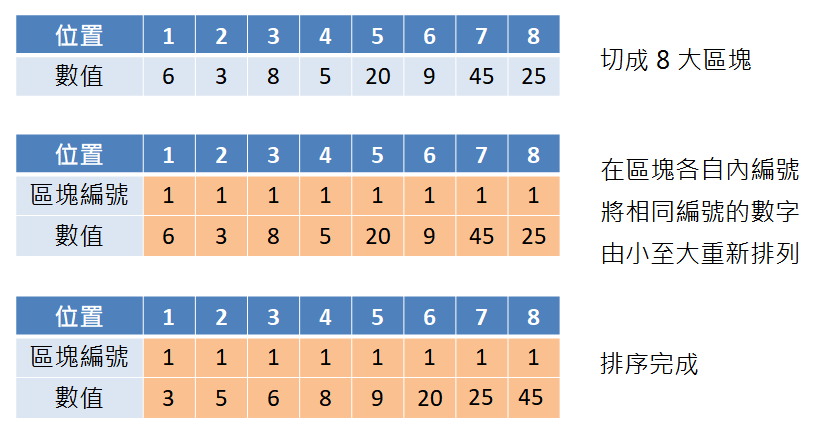
• 步驟三
  區間值 = 1，可區分成 4 個區塊，每個區塊含有 2 個數字，記得最後一個步驟區間值一定要是 1，所以每個數字的編號都是 1，則會全部一起排序，則依序由小到大排列完成
  

今日小結

看似簡單的排序，背後其實很多因素要考量，種類非常多種，有時候真的不方便記憶，所以除了透過生活例子之外，也要多多認識了解排序演算法的內容，未來有需求時可以自行評估，選擇適合自己的演算法去實作相關需求

今日謎題

演奏會的傳單中寫著演奏家的名字謝耳，並寫著 6 個神秘數字：4, 2, 3, 5, 3, 2，區間值 = 3，由大至小排序的過程中，你能察覺出他要演奏什麼歌曲嗎？

昨日解謎

謎題說明：將數字15, 3, 12, 5, 12，由小至大排列會得到 3, 5, 12, 12, 15，然後查數字與英文字母的表格，會得到 CELLO 大提琴，你答對了嗎？