今天要來介紹費式搜尋法,老實說我完全沒印象以前老師有教過這個,自己看了兩天才終於看懂,看起來很複雜,事實上真的很複雜XD
你有欣賞過花朵嗎?有沒有注意到,有些花的花瓣大多是 3 瓣或 5 瓣,也有 8 瓣或 13 瓣,為什麼會這些數字這麼常出現呢?似乎是大自然的一種法則
圖片來源:https://www.pexels.com/zh-tw/photo/4621593/
或是某些建築例會呈現黃金比例,其實都是費氏級數的呈現
圖片來源:https://unsplash.com/photos/zHDiLstmQwo
在介紹費式搜尋法之前,先來了解一下費氏級數或稱斐波那契數列
公式
根據公式只會用到加減運算,不需要進行乘法與除法,所以效率會比較好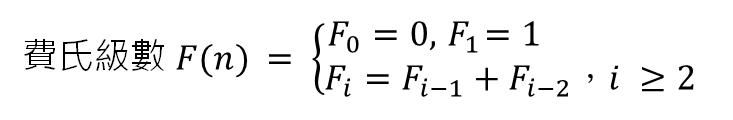
數列
數列有 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...,除了最前面的兩個數值 0 與 1 之外,其他數值皆為前兩個的相加,例如 8 = 5 + 3
費式搜尋法又稱費伯那搜尋法,跟內插搜尋法一樣會透過某個公式來限縮搜尋範圍,內插搜尋法是透過斜率公式,而費式搜尋法是使用費式級數來分割,可參考維基百科的說明
相差值會等於某一個費氏數值左節點的數值會小於父節點右節點的數值會大於等於父節點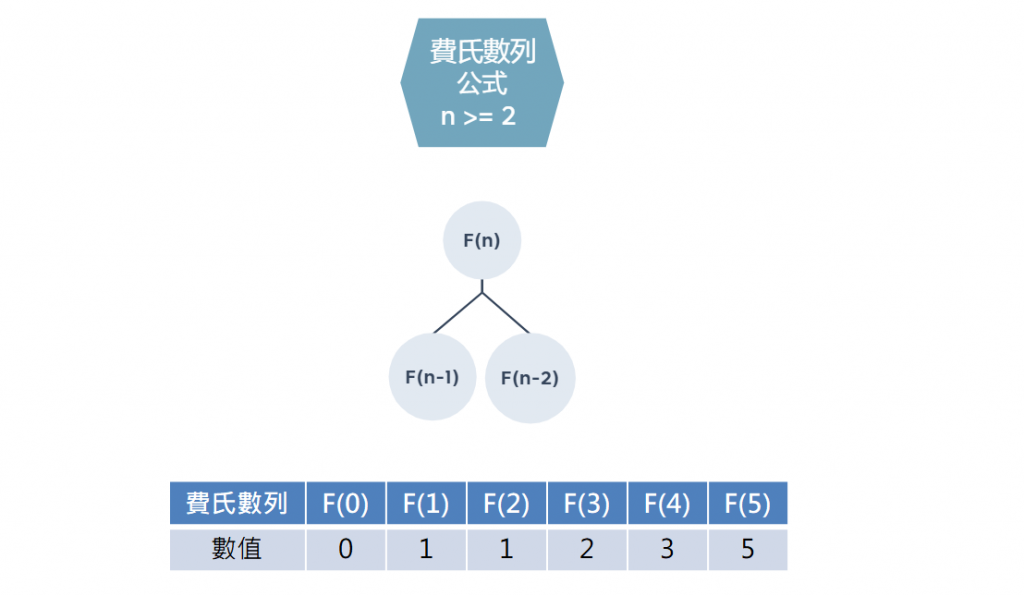
會發現左圖的二元樹節點到F(1)就會停止,因為沒有符合 1 小於 2 了,就沒有符合 n 大於等於 2 的公式了,再將數列中的數值逐一帶入二元樹中,觀察右圖即可發現樹根的數值 = 左右節點相加的數值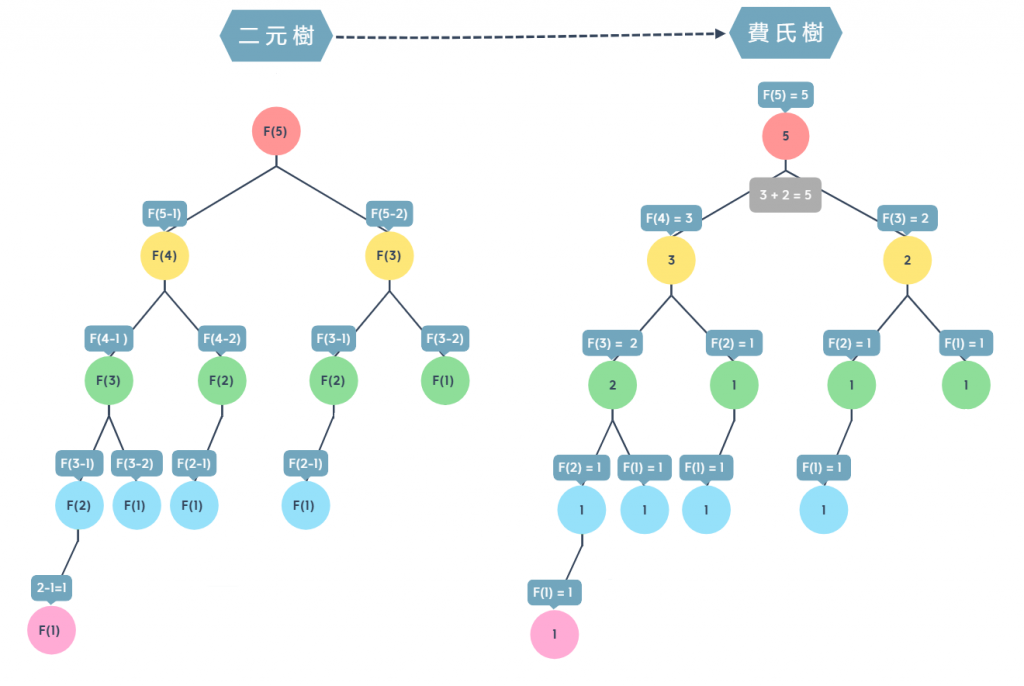
資料置放的順序
存入資料數據之前,要先取得資料置放的順序,使用中序走訪費氏樹,可觀察到父節點與左右節點之間有一個固定的相差值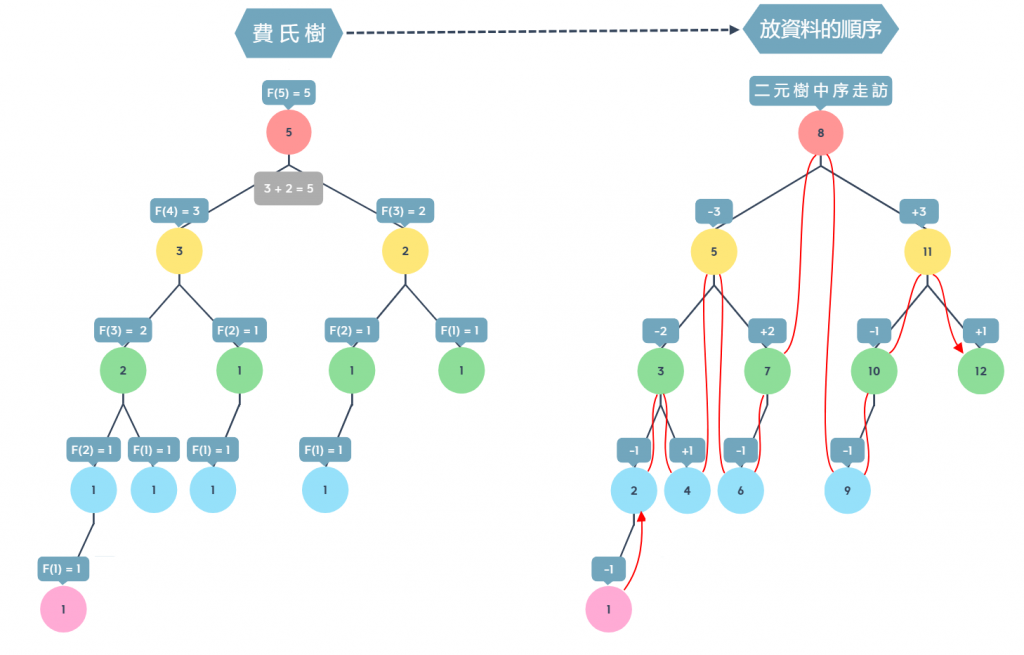
相差值
公式如下,其相差值為某一個費氏級數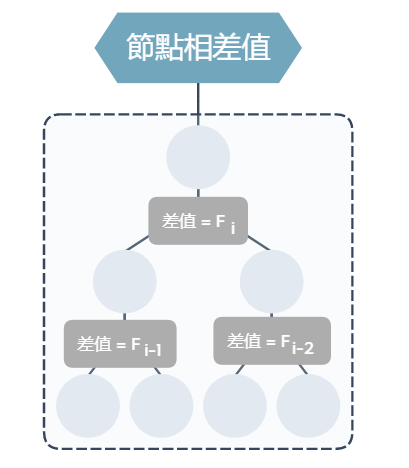
將要搜尋的資料由小至大放到費式樹中,例如,有一由小到大排列好的數列:2, 5, 17, 26, 38, 42, 59, 60, 65 ,72 ,87, 93,共 12 筆資料
使用多少節點來儲存呢?可透過以下公式求得最大費氏數,其中的 n 為資料筆數,12 + 1 = 13,就去查表看看哪個費氏級數的數值大於或等於 13,可找到 F(7) = 13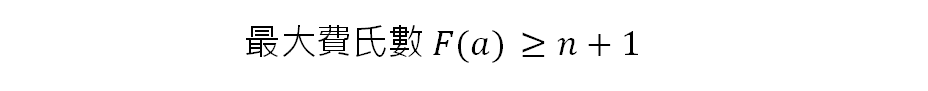

搜尋要從樹根結點,樹根位置可套用公式 F(a-1),上面我們以求得 12 筆資料的最大費氏數為 F(7),則樹根位置為 F(7-1) = F6 = 8,所以樹根在索引位置 8 的地方,然後將此位置的數值與想要找的數值相比,則可決定要繼續往左子樹還是右子樹搜尋,公式如下:小於等於樹根節點的數值時,往左子樹找大於樹根節點的數值時,往右子樹找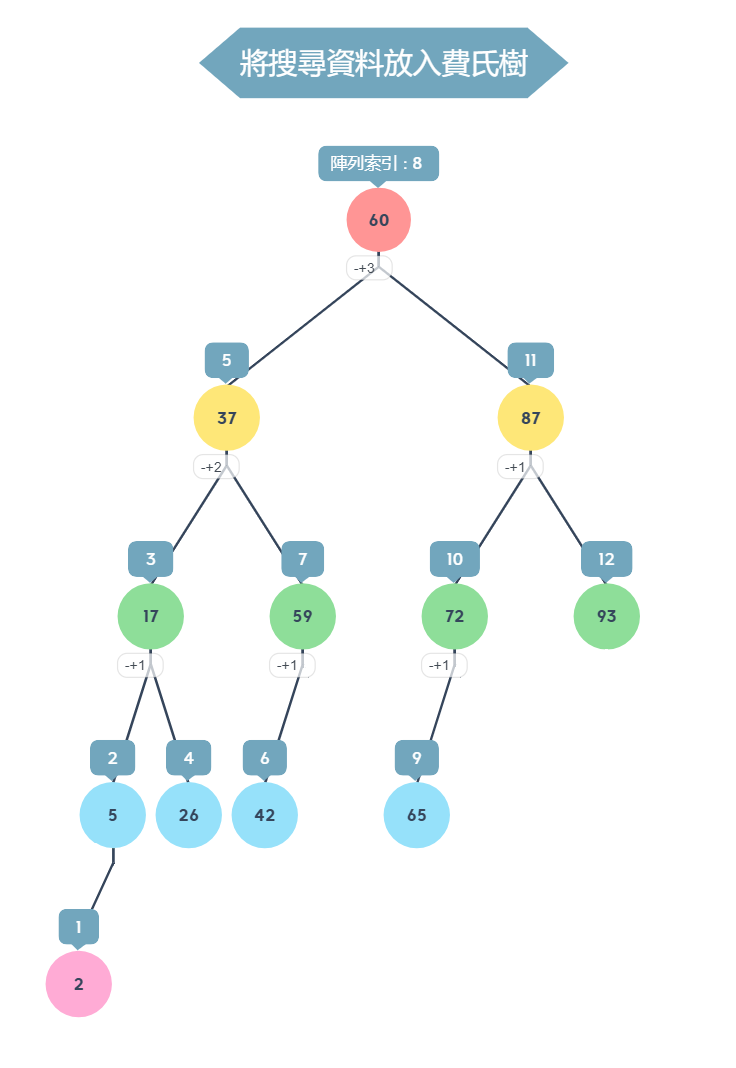
樹根位置為 F(7-1) = F6 = 8,將 26 與陣列索引 8 的數值相比,發現 26 小於 60,繼續往左子樹找左子樹樹根減去相差值 3 , 8 - 3 = 5 ,將 26 與陣列索引 5 的數值相比,發現 26 小於 60,繼續往左子樹找左子樹樹根減去相差值 2 , 5 - 2 = 3 ,將 26 與陣列索引 3 的數值相比,發現 26 大於 17,繼續往右子樹找右子樹樹根加上相差值 1 , 3 + 1 = 4 ,將 26 與陣列索引 4 的數值相比,發現 26 等於 26,成功找到數值,位於陣列索引 4 的位置平均狀況下效能優於二分搜尋法,但最壞的情況下會筆二元搜尋法還慢
費式搜尋法實作上比較複雜,還要先產生費氏樹,樹根與左右節點之間又有許多關聯,雖然是不錯的搜尋法,但實作上要考慮的事情會比較多一點,這否方便維護也是需要考量的地方,給大家參考看看囉
今天有一神秘數列:1, 1, 2, 3, 5, 8, 13, ...,你是不是已經猜到答案了?沒錯!就是今天內文有提到的費氏數列,但今天不是要猜費氏數列 XD
小美的數學老師提供了這段數字給班上的同學:1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, ? ,小美一直解不出問號處的數字,你能幫助小美找到答案嗎?
謎題說明:練習插入的概念,選擇合適的運算符號,嘗試讓公式成立,答案為 12 + 3 - 4 x 5 + 6 = 1,你答對了嗎?
