前言

圖形也有搜尋演算法可以使用，例如深度優先搜尋法與廣度深度優先搜尋法，一起來看看吧

生活常識

你在超市購物時，都是怎麼選購貨架上的物品？是使用左右掃射，還是上下掃瞄呢？哪一種方式可以最快找到你想買的東西呢？

圖片來源:https://www.pexels.com/zh-tw/photo/1005638/

你玩過迷宮嗎？這是個很考驗運氣、耐性、智慧與勇氣的遊戲，從起點走到終點，會出現很多路徑，面臨多條路徑的選擇時，常常會出現選擇障礙，因為如果選錯可能就會走回頭路，你會怎麼決定你的策略呢？

1. 隨機選一條路之後就勇往直前等遇到死路在做打算，
2. 每個路徑會先去探一小段路之後再做打算

不管是哪一種，都很有可能走得頭昏眼花、四肢不聽使喚，最後還不見得能順利過關XD，不知道你有沒有聽過一種可以快速破解迷宮的方法，叫做沿牆走，不過只適用於某些類型的迷宮，最土法煉鋼的方式就是勇敢嘗試，試到最後面一定會找到出口，只怕時間不夠或是你已經感到心疲力竭先放棄了，那要怎麼預防迷路呢？可以學習童話故事中丟麵包屑的方式，讓自己清楚知道要注意哪些路徑

圖片來源:https://www.pexels.com/zh-tw/photo/1904204/

專業知識

圖形說明

如果對於樹或圖形結構不熟悉的話，可以參考前幾天的文章，圖形是由許多頂點與邊組成的，而樹也是圖的一種，當今天我們在某著頂點，想要到達某個頂點時，會經過某些路徑，而要如何快速找到這兩個頂點之間的相連路徑，就是演算法要做的事情

判斷是否走過

由於目標頂點位於圖形的哪個位置我們並不知道，檢查該頂點是不是我們要尋找的頂點，在搜尋過程中為了清楚知道哪些頂點是已經搜尋過的(就像走迷宮可以丟麵包屑或做記號)，我們必須透過其他的資料結構堆疊、佇列或是使用遞迴演算法來輔助我們記憶已訪問過的頂點或路徑，才不會做重覆性的搜尋

深度優先搜尋法 Depth-first Search

選擇路徑

如果要找 A 走到 G 的路徑，請找一個與 A 相鄰的點且沒有走過的點，重覆以下兩個動作直到找到目標點或所有點都被走過為止

• 有找到：判斷是否為目標點，如果不是則將此點紀錄為已走過，並以此點為新的點，再繼續往下找與新點相鄰且沒有走過的點，例如， B 與 A 相鄰，B 不是 G 點，所以再去找與 B 相鄰的點，找到 C
• 沒找到：回到前面的點，然後再去找到其他沒有走過的相鄰點做搜尋，例如，與 C 點相鄰的點都走過了，還是找不到 G 點，那就要回到 B，再去找與 B 相鄰且沒有走過的點

例子

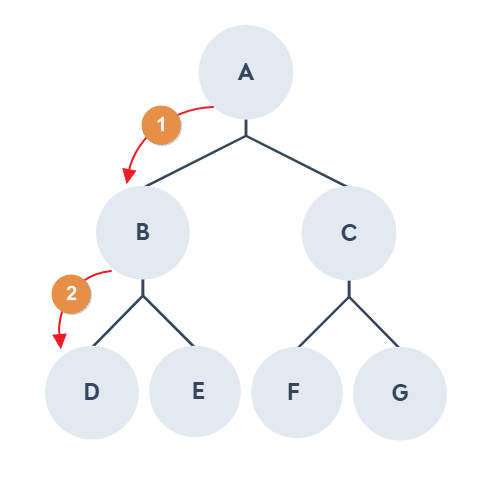
如果以二元樹作為例子，其實搜尋方式就很類似前序走訪，例如從節點 1 走到節點 6，如果這是一個迷宮，使用深度搜尋實際走的樣子會長這樣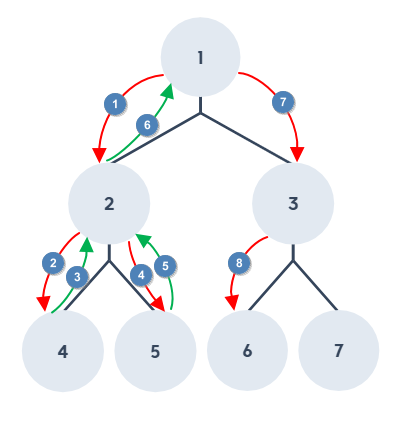

只是要特別注意的是走訪過的節點不能再度走訪，所以使用堆疊後進先出的特性來記錄還沒有走過的節點，如果忘記堆疊的可以參考前幾天的文章

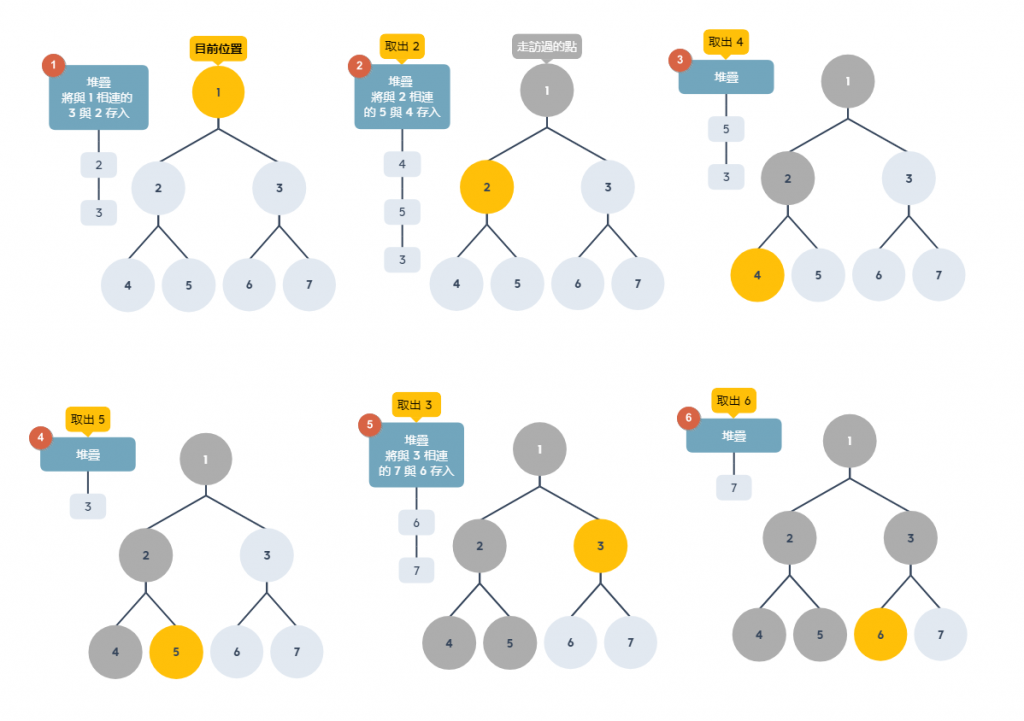
由上圖可發現，深度優先會一直往下一層搜尋，直到樹葉節點還找不到未走過的節點時，才會往上一層找沒有走過的節點，搜尋順序為：1、2、4、5、6、6、7

廣度優先搜尋法 Breadth-first Search

選擇路徑

如果要找 A 走到 G 的路徑，請找一個與 A 相鄰的點且沒有走過的點，重覆以下兩個動作直到找到目標點或所有點都被走過為止

• 有找到：判斷是否為目標點，如果不是則將此點紀錄為已走過，並回到上一個基準節點去尋找其他與基準節點相鄰的點，例如，A 為基準點 B，A 與 B 相鄰，但 B 不是 G 點，所以需要回到 A 點，再去找與 A 相鄰且沒有走過的點，會找到 C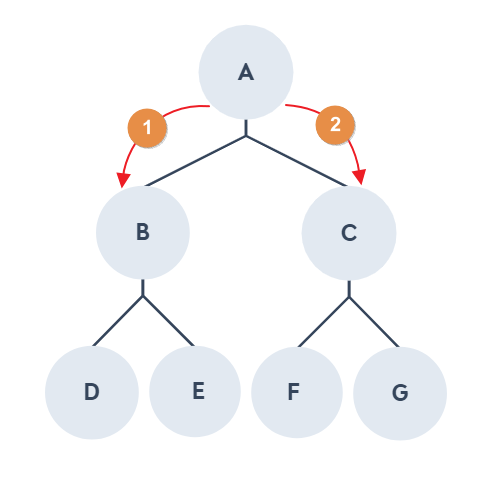
• 沒找到：表示與基準節點相鄰的點都不是目標點，則找新的基準點，例如，以 A 為基準點的相鄰節點都走過了，則可使用 B 當作基準點，再去找與 B 相連的節點

例子

如果以二元樹作為例子，其實搜尋方式如下圖，例如從節點 1 走到節點 6，如果這是一個迷宮，使用廣度搜尋實際走的樣子會長這樣

只是要特別注意的是走訪過的節點不能再度走訪，所以使用佇列後進先出的特性來記錄還沒有走過的節點，如果忘記佇列的可以參考前幾天的文章

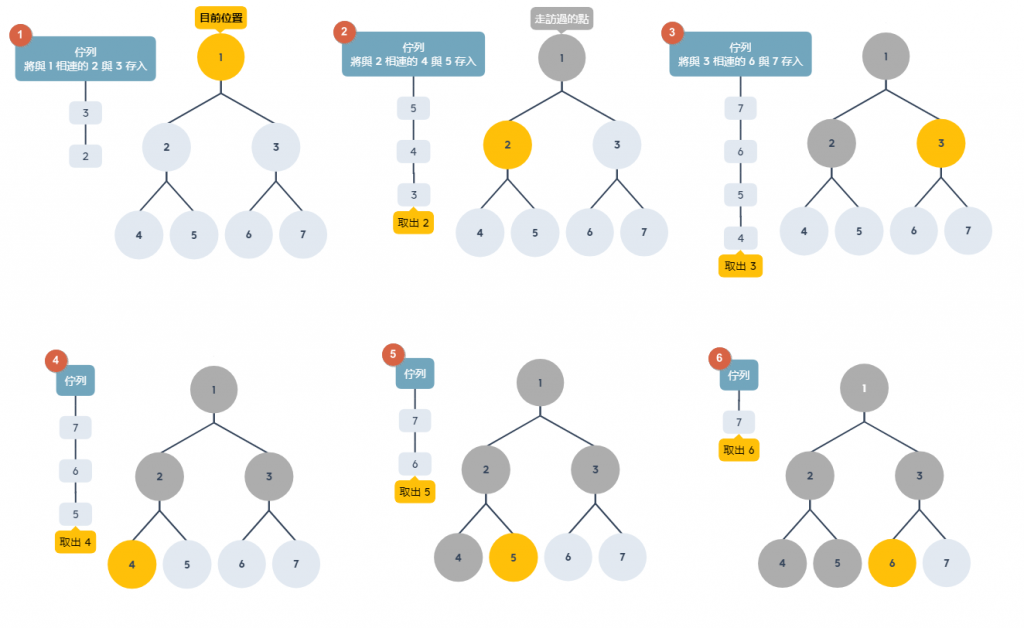
由上圖可發現，廣度優先會往同一層搜尋，直到找不到未走過節點時，才會往下一層找沒有走過的節點，搜尋順序為：1、2、3、4、5、6、7

今日小結

深度與廣度誰比較好呢？其實還是要看使用的情境，如果已經有個很明確的目標，那深度也許是不錯的選擇，但資源有限的情況下，可能廣度會比較好，個人看法，參考參考XD

今日謎題

小美遇到的人生的十字入口，入口位於下圖的上方，有三個入口，行經路線只要經過線條，就必須強制轉彎，途中會經過許多字母，其中一條路可以組成一個有意義的單字，小美不知道該如何選擇，請問你能幫他找到對他最有意義的一條路徑嗎？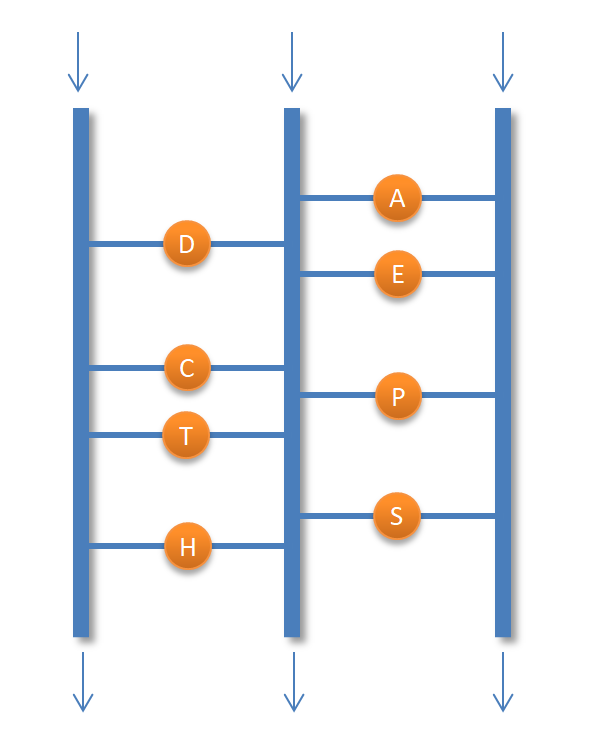

昨日謎題

謎題說明：認識到費式數列的規則之後，再去認識其他的類似也有其他規則的數列，這段數列 1, 1, 1, 2, 2, 3, 4, 5, 7, 9, 12, 16, ？，其實是巴都萬數列

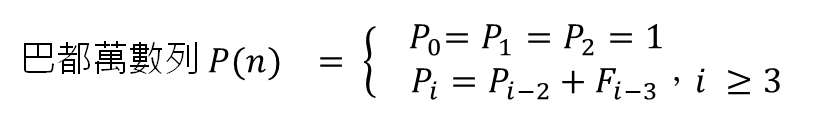
簡單來說，P(3) = P(1) + P(0) = 1 + 1 = 2，也就是說每一個數字，都是由往前推的第三個數字與第二個數字相加而來，再舉一個例子，16 = 7(往前推的第三個數字) + 9(往前推的第二個數字)，所以問號處的數字會由 9 + 12 而組成，所以答案是 21，你答對了嗎？