前言

今天要來介紹內插搜尋法，這個名字聽起來就很抽象，不容易知道這個演算法是如何進行搜尋的，一起來認識它吧！

生活常識

唸大學的時候，如果可以自由挑選座位，你都是做在哪邊的位置上呢？是挑前面的位置認真上課，還是挑後面的位置方便翹課XD，想必你對於坐前面或坐後面有一套自己的挑選方式，而如果是站在授課老師的角度，老師會挑選坐前面的學生來回答問題，還是挑後面的學生來回答問題呢？如何在教室內挑到一位合適的學生來回答不同難易程度的問題，這真的是很考驗老師的搜尋能力，感覺坐越前面的參與度越高，越後面的參與度越低，到底要挑選哪一區的哪一位同學來回答，想必老師也有一套挑選學生的方式

圖片來源:https://www.pexels.com/zh-tw/photo/207691/

專業知識 - 內插搜尋法 Interpolation Search

內插搜尋法又稱插補搜尋法，主要是針對已排序的資料進行搜尋，算是二分搜尋法的改良版本，二分法會先找中間值，但內插搜尋法會透過斜率公式初步估算資料可能出現在哪個的位置，很像在一個範圍內插入一個可能的位置，並逐漸縮小搜尋範圍

斜率公式可參考維基百科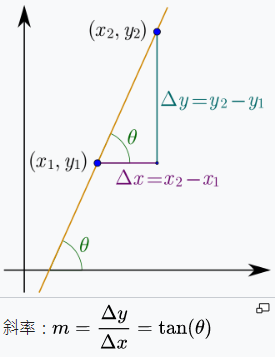

圖片來源:https://zh.wikipedia.org/wiki/%E6%96%9C%E7%8E%87

插補搜尋法公式

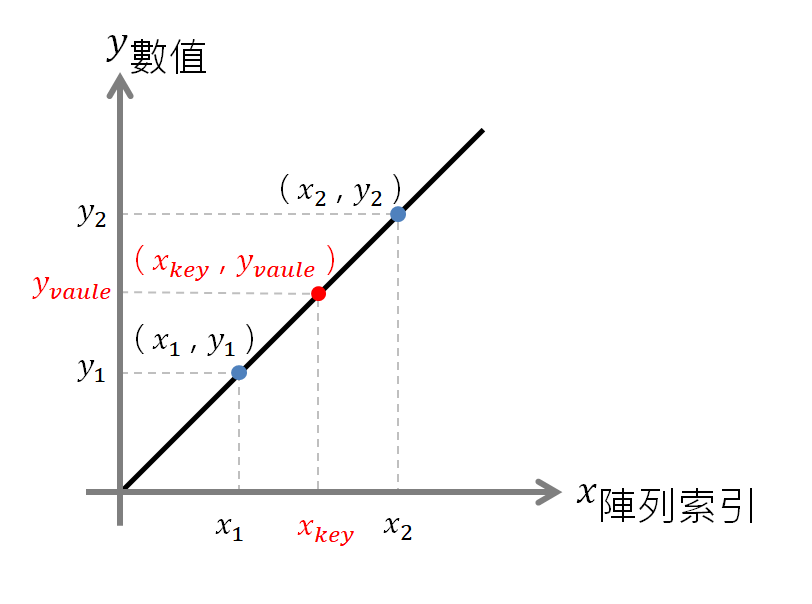
假設 X 軸為陣列索引，Y 軸為由小到大排列的儲存的數值，我們可藉由終點(x2, y2)與起點(x1, y1)的斜率會等於目標點(x-key, y-value)與起點(x1, y1)的斜率`去推出資料可能的位置

例子

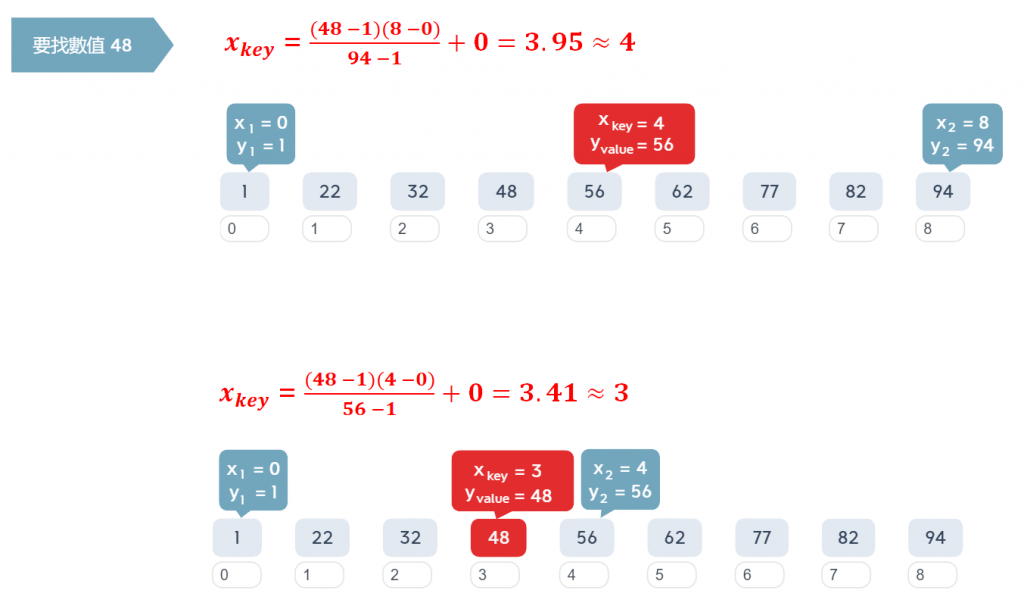
有一數列：1, 22, 32, 48, 56, 63, 47, 82, 94，共 9 個數值，由小到大排列，要找 48 在哪裡，套用公式時，若求出來的值有小數點則四捨五入(或使用你習慣的方式處理小數點也可以)，以下分為兩個步驟進行搜尋：

1. 第一次的公式代入得到 X 軸 = 4 ，則去找陣列索引 4 的位置，找到的數值為 56 ，56 不等於 48，繼續搜尋
2. 第二次的公式代入，得到數值 X 軸 = 3，則去找陣列索引 3 的位置，找到的數值為 48 ，48 等於 48，成功找到數值則結束搜尋

分析

效能的好壞取決於數值的分佈，如果資料分佈的越平均，搜尋速度就越快，

• 最壞的情況
  O(n)，資料分佈不平均

• 最好的情況
  Ο(log2n)，每次搜尋可減少一半的資料量

今日小結

內插搜尋法在資料分佈均勻時真的蠻快的，但分佈不均勻時跟循序搜尋法差不多，要特別注意資料的分佈情況是否均勻

今日謎題

123456 = 1 這個等式是錯的，你知道如何在 12、3、4、5、6 之間插入四個運算符號(只能用加號、減號或乘號)，使等式成立嗎

昨日解謎

謎題說明：主要是希望大家可以體會一下二分搜尋法中的對半切動作，將下圖資料對半切，然後只看右半部，就可以觀察到 2576 這四個數字，你猜對了嗎？