跟前一天所介紹的模糊集也很像
粗糙集是用來逼近一個明確集合用
如下圖所示

(以下例子來自 New approaches to fuzzy-rough feature selection)
我們可以利用模糊集找一些規則
以下表為例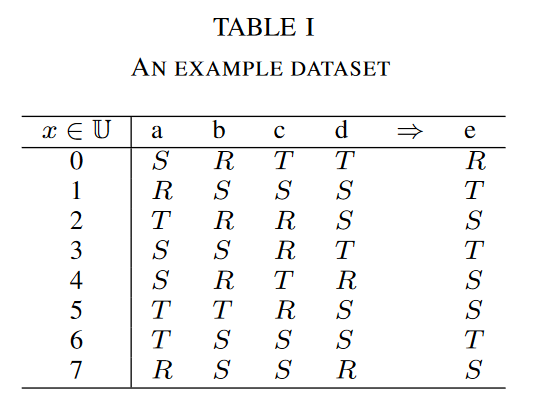

其中 為樣本編號
a,b,c,d,e 為樣本的觀察特徵

如果現在用特徵 b 對 U 做分類可得
因為 {0,2,4} 在特徵 b 都是 R，而 {1,3,6,7} 在特徵 b 都是 S，而 {5} 在特徵 b 都是 T

如果用特徵子集 {b, c} 對 U 做分類可得
理由類似上個舉例

如果把想要對 U 做分類用的特徵子集稱作 P
則用特徵子集 P 對 U 做分類可得 U/P (我自己是習慣念 U quotient P)
如上述兩個例子， U/P 是一個集合，且這個集合的元素為集合
另外可以對 U/P 中的元素(現在是一個集合)，取其中一個元素 x (現在是一個樣本編號)簡記成

例如用特徵子集 P = {b, c} 對 U 做分類可得
則 且
簡單的說就是在特徵子集 P 之下是等價類~XD

既然等價，就拿一個當代表就好
就像「奇數」就是 任意整數除以 2 餘 1
所以可以用 1 來代表奇數
記成 來表示奇數

明天再來說他接下來做模糊集的部分