1　前言

近年來深度學習使用在許多比賽中，但幾乎都使用ensemble(集成)的方式或是使用龐大的模型，這有個很嚴重的問題，那就是成本過高無法落地(除了原本就很昂貴的設備)，因此近幾年也有許多人設計適用於嵌入式裝置的模型，而Neural Architecture Search(NAS)便是解決辦法之一，它能自動搜尋模型架構找到較為適合的架構，並且在效能上也能夠有一定的表現，甚至有些NAS在訓練時也能限制FPS和模型大小等等，如此一來在嵌入式裝置也能夠輕易地使用並且獲得好的效能。

此篇文章要介紹的是Sequential Greedy Architecture Search(SGAS)[1]，SGAS是基於gradient descent(梯度下降演算法,GD)來找架構，這裡我使用Convolutional neural network(CNN)作為範例 ，除了GS以外還有evolutionary algorithm (演化是演算法, EA)和reinforcement learning(強化學習,RL)等等方式能夠找架構。想了解更多可參考AutoML Survey[2]。

2　SGAS貢獻

首先簡單的先了解SGAS的貢獻。

1. 使用貪婪的方式進行剪枝。
2. 使用三種計算方式來定義剪枝的優先度，分別Edge Importance(重要性)、Selection Certainty(確定性)和Selection Stability(穩定性)三種計算來增加模型訓練的穩定性。

3　SGAS演算法

3.1　Cell(Block)

註:假設Cell和Block是相同的東西
在開始進入SGAS時要先知道什麼是Cell(Block)，因為SGAS是在找出一個可能較好的Cell(Block)。這裡使用Resnet[3]為例，我們常常會聽到ResNet18/34/50/101/151...，而後面數字是代表經過了Ｎ層的運算層，其中運算層如卷積層和池化層等等，而Cell其實就是將幾個運算層組合起來，如下圖一(a)為ResNet-38的Cell，由此可知道ResNet-38是使用許多個Cell(a)所堆疊起來的網路，同理可知圖一(b)也是一樣，除此之外不同的Cell也會得到不同的效能。因此有許多人設計了不同的Cell來提升效能，而這篇論文是使用可微分與可加性來去找出最佳的Cell，如此一來能夠因應不同的資料集並且減少人工設計的成本。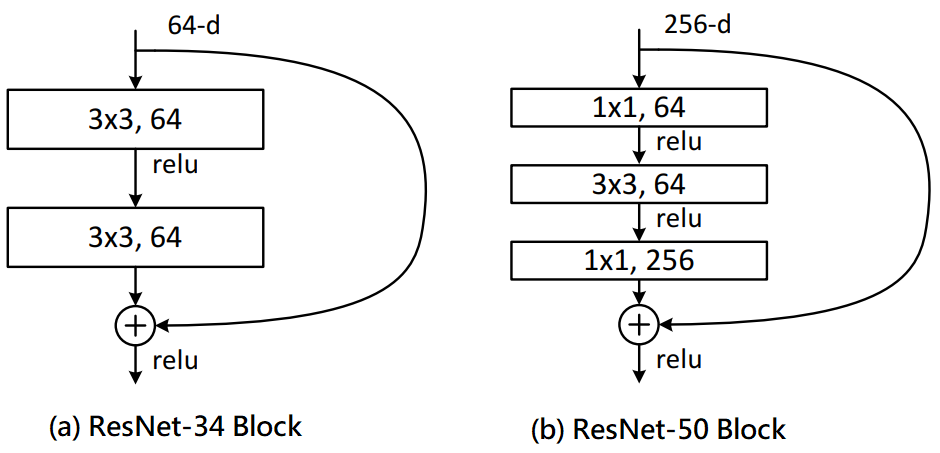

圖一，來源[3]。

3.2　SGAS流程

從ResNet上面可以看到每一個箭頭代表著一種運算層，而在SGAS中則是先定義N種運算層(3x3卷積層、最大池化層、5x5卷積層...)，也就是說第N層到第N+1層從原先只計算一個運算層變為需要計算N個運算層，如圖二(a)，不同顏色的箭頭代表著不同的運算層，而N個運算層會乘上一個對應的權重(訓練出來的)做相加。

接著會先經過訓練後，在N個運算層中選出一個較為重要的運算層，其餘的則忽略，而這就是剪枝，如圖二(b)，經過Greedy Decision在第0個節點和第1個節點選出藍色線，再來經過訓練後相同的經過Greedy Decision選擇要剪枝的節點，如圖二(c)，反覆此步驟直到每個節點都剪枝完畢，如圖二(d)。

簡單的例子：假設輸入(1, 3, 32, 32)大小的資料。

• ResNet會輸出是(1, 64, 32, 32)。
• 未剪枝的SGAS會有N個運算層則會變為[(1, 64, 32, 32), (1, 64, 32, 32)...N]，在乘上相對應的權重[0.1, 0.05...N]做加總，所以輸出的大小一樣是(1, 64, 32, 32)。
• 已剪枝的SGAS只會有一個運算層，所以輸出的大小是(1, 64, 32, 32)。

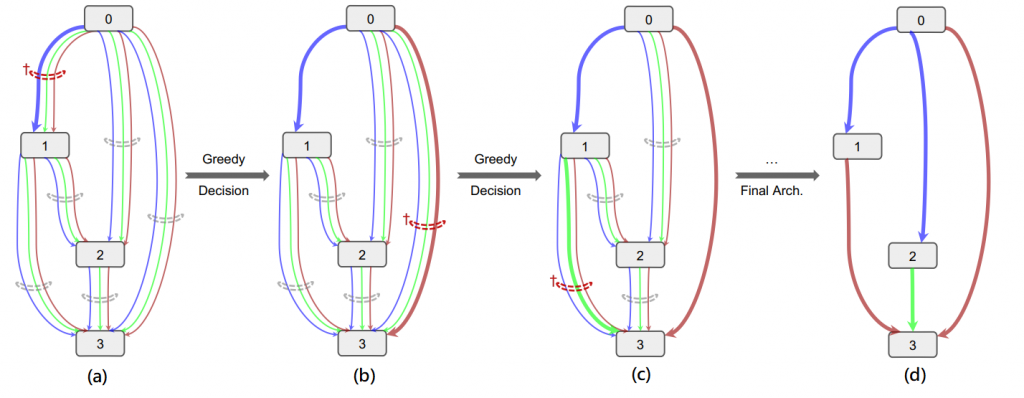
圖二，來源[2]。

3.3　SGAS演算法

這裡直接附上SGAS演算法，如圖三，其中i和j代表著不同的節點，alpha代表運算層的重要度(權重)，W代表整體網路的權重，這裡與上述的流程是相同的，只是用演算法的形式寫出。

1. 使用驗證集更新A(每一個alpha)。
2. 使用訓練集更新W。
3. 經過Greedy Selection Criterion找出最大值的節點進行剪枝，剪枝過的alpha則不再更新。
   
   圖三，來源[2]。

3.3.1　Greedy Selection Criterion Formula

SGAS主要使用了三個公式作為Greedy Decision的選擇標準。

• Edge Importance
  第一個公式為計算alpha(i, j)的重要性，其中i、j為不同的節點。上述有提到每一次計算有N個運算層，而其中有一個運算層為non-zero層，也就是說經過non-zero層後的輸出等於零，反向傳播(偏微分)時的梯度一樣為0，因此能夠說如果alpha(i, j)的non-zero層的權重較大，代表著此層的重要程度是比較小的。詳細公式如公式一。
  註:使用exp能將連乘的機率轉為相加。

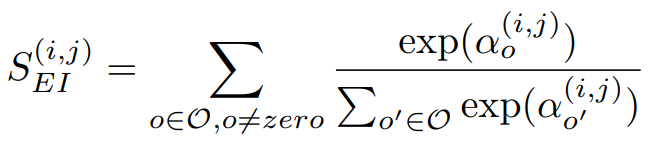
公式一，來源[2]。

• Selection Certainty
  第二個公式為計算alpha(i, j)的確定性，其中i、j為不同的節點。公式二則延續公式一，只是多使用entropy來計算平均的確定性。詳細公式如公式二。
  這裡舉個簡易的例子來看出entropy的特性，其中entropy公式為x*log(x)，可以看到越接近1或0的entropy都會比較大，因此能夠利用entropy的特性來計算出不確定性(越接近0確定性越大)。而要計算確定性只要加上1即可。
  1.機率為0.9的entropy為0.9 * log(0.9) = -0.04，反之確定性=0.96。
  2.機率為0.1的entropy為0.1 * log(0.1) = -0.1，反之確定性=0.9。
  3.機率為0.5的entropy為0.5 * log(0.1) = -0.15，反之確定性=0.85。
  上述的例子可以得知0.5的不確定性較大，可以反應出未收斂或模型產生矛盾等等情況。
  註:計算一次極端狀況能知道Selection Certainty是補足Edge Importance的不足。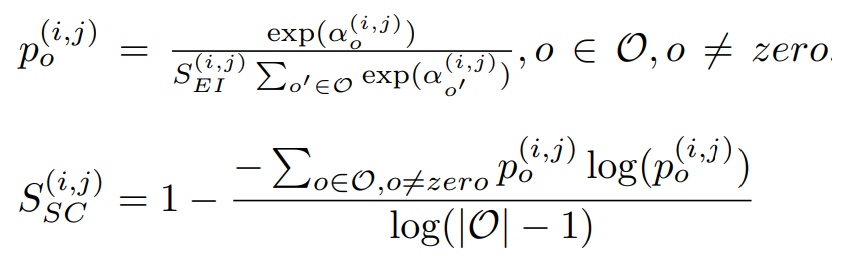
  
  公式二，來源[2]。

• Selection Stability
  第二個公式為計算alpha(i, j)的穩定性，其中i、j為不同的節點。若只考慮公式一和公式二，可以知道兩者僅僅只考慮當下的alpha(i, j)，這有可能會產生不穩定情形，例如第一次決策時的機率是0.1，第二次決策時的機率是0.9，第三次0.1，第四次0.9，這時就會有不穩定的情況，因此SGAS考慮了Ｔ個歷史紀錄，用來計算彼此的交集，這樣能夠將穩定度也考慮進去。詳細公式如公式三。

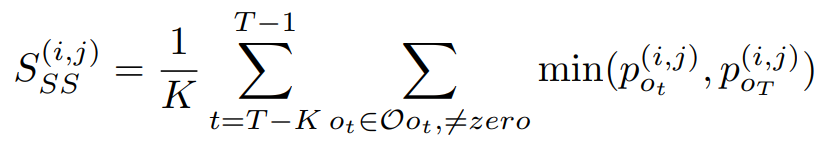
公式三，來源[2]。

3.3.2　Greedy Selection Criterion

SGAS使用了上述三個公式做評估，假設都是獨立機率則相乘即可獲得分數，而分數又分為Cri.1公式四和Cri.2公式五，差別在於有無考慮歷史訊息(Selection Stability)。

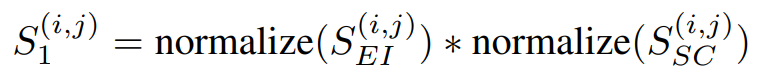
公式四，來源[2]。

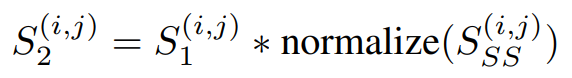
公式五，來源[2]。

4　主要程式碼解析

4.1　Network

GitHub位置:/sgas/cnn/model_search.py

其它參數

一般的網路運算層基本上只有一個運算層，如3x3卷積層、5x5卷積層、3x3空洞卷積層....，而SGAS運算層定義為包含八種運算層，如下。

PRIMITIVES = [
    'none',
    'max_pool_3x3',
    'avg_pool_3x3',
    'skip_connect',
    'sep_conv_3x3',
    'sep_conv_5x5',
    'dil_conv_3x3',
    'dil_conv_5x5'
]

主要函數

MixedOp：當無選擇的索引(未被剪枝)則計算八種運算層乘上權重的合，若有選擇的索引(已剪枝)則選擇該層運算做為輸出。

class MixedOp(nn.Module):
    def forward(self, x, weights, selected_idx=None):
        if selected_idx is None:
            return sum(w * op(x) for w, op in zip(weights, self._ops))
        else:  # unchosen operations are pruned
            return self._ops[selected_idx](x)

Cell：SGAS用兩個Node做為輸入，分別是前一個Cell的輸出(s0)，現在Cell的輸出(s1)，這種想法其實有點類似ResNet和DenseNet，甚至未來可以嘗試使用CSPNet的想法來減少計算量，而這裡的**_steps表示操作次數，可以當作是Cell深度的上限(預設4)，每計算一次就可以得到更高階的特徵，並且會將輸出加入states list內以供下次操作使用，這裡其實也隱含著類似ResNet和DenseNet**的想法，因為下一層還能夠使用上一層的輸入進行運算，可以讓網路自行決定要使用低階特徵或是高階特徵。

註:這裡特別的地方是states list的數量隨著增加，但輸出的數量是不變的，因為會將所有states list經過MixedOp的輸出進行相加，這想法也就是特徵融合。

class Cell(nn.Module):
    def forward(self, s0, s1, weights, selected_idxs=None):
        s0 = self.preprocess0(s0)
        s1 = self.preprocess1(s1)

        states = [s0, s1]
        offset = 0
        for i in range(self._steps):
            o_list = []
            for j, h in enumerate(states):
                if selected_idxs[offset + j] == -1: # undecided mix edges
                    o = self._ops[offset + j](h, weights[offset + j])
                    o_list.append(o)
                elif selected_idxs[offset + j] == PRIMITIVES.index('none'): # pruned edges
                    continue
                else: # decided discrete edges
                    o = self._ops[offset + j](h, None, selected_idxs[offset + j])
                    o_list.append(o)
            s = sum(o_list)
            offset += len(states)
            states.append(s)

        return torch.cat(states[-self._multiplier:], dim=1)

Network _initialize_alphas:初始化每一個Cell內的運算層權重，與上述Cell迴圈相同，而產生亂數的大小是運算層種類大小(8種運算)，而這裡較為特別的地方是，分為alphas_normal和alphas_reduce權重，alphas_normal代表無需下採樣的Cell，而alphas_reduce代表需要下採樣的Cell，(部份研究)會分為兩個區塊的原因可能是下採樣通常會設定不同的stride或池化層等等，因此這操作與無須下採樣的Cell是稍微不同的，所以會分為兩個區塊進行。

Network forward:會先計算alphas權重，再呼叫Cell進行計算，與一般網路差別在於權重。

Network check_edges:在剪枝完後呼叫，會限制每一次操作(深度)，若以有max_num_edges個已決策的節點則其餘節點可以忽略。這個函數在限制計算複雜度，而當限制越寬鬆(max_num_edges越大)則運算量越大與訓練時間越久。

class Network(nn.Module):
    def _initialize_alphas(self):
        k = sum(1 for i in range(self._steps) for n in range(2 + i))
        num_ops = len(PRIMITIVES)

        self.alphas_normal = []
        self.alphas_reduce = []
        for i in range(self._steps):
            for n in range(2 + i):
                self.alphas_normal.append(Variable(1e-3 * torch.randn(num_ops).cuda(), requires_grad=True))
                self.alphas_reduce.append(Variable(1e-3 * torch.randn(num_ops).cuda(), requires_grad=True))
        self._arch_parameters = [
            self.alphas_normal,
            self.alphas_reduce,
        ]
        
    def forward(self, input):
        s0 = s1 = self.stem(input)
        for i, cell in enumerate(self.cells):
            if cell.reduction:
                selected_idxs = self.reduce_selected_idxs
                alphas = self.alphas_reduce
            else:
                selected_idxs = self.normal_selected_idxs
                alphas = self.alphas_normal

            weights = []
            n = 2
            start = 0
            for _ in range(self._steps):
                end = start + n
                for j in range(start, end):
                    weights.append(F.softmax(alphas[j], dim=-1))
                start = end
                n += 1

            s0, s1 = s1, cell(s0, s1, weights, selected_idxs)

        out = self.global_pooling(s1)
        logits = self.classifier(out.view(out.size(0), -1))
        return logits

    def check_edges(self, flags, selected_idxs, reduction=False):
        n = 2
        max_num_edges = 2
        start = 0
        for i in range(self._steps):
            end = start + n
            num_selected_edges = torch.sum(1 - flags[start:end].int())
            if num_selected_edges >= max_num_edges:
                for j in range(start, end):
                    if flags[j]:
                        flags[j] = False
                        selected_idxs[j] = PRIMITIVES.index('none') # pruned edges
                        if reduction:
                            self.alphas_reduce[j].requires_grad = False
                        else:
                            self.alphas_normal[j].requires_grad = False
                    else:
                        pass
            start = end
            n += 1

        return flags, selected_idxs

4.2　Architect

GitHub位置:/sgas/cnn/architect.py
Architect有使用到unrolled來控制是否要添加train data的hessian矩陣(梯度的方向)到優化器內，而這並不是該論文重點(預設false，其它dataset訓練也無使用)，因此就先略過，有興趣可找相關文獻觀看。

主要函數

使用validation data更新未剪枝的的alphas權重。(神經網路無更新)

class Architect(object):
  def _backward_step(self, input_valid, target_valid):
    loss = self.model._loss(input_valid, target_valid)
    loss.backward()

4.3　Train

GitHub位置:/sgas/cnn/train_search.py
現在知道主要的Network架構也知道驗證更新參數時使用的是Architect，接著就是greedy decision的算法，這裡就按照上述所講的演算法和公式一步一步的講解。

1.train

訓練所對應的演算法就是1.使用validation data來更新alpha和2.使用train data來更新weights。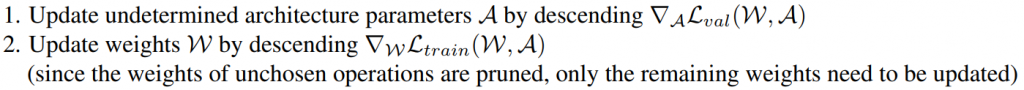

參數：
train_queue：train dataloader(Pytorch Class)
valid_queue：validation dataloader(Pytorch Class)
model：train model
architect：class of update alpha
input：train data
target：train target
input_search：validation data
target_search：validation target

def train(train_queue, valid_queue, model, architect, criterion, optimizer, lr, epoch):
    ...

        # Algorithm 1. Update undetermined architecture parameters(only alpha)
        architect.step(input, target, input_search, target_search, lr, optimizer, unrolled=args.unrolled)
        
        # Algorithm 2. Update weights W
        optimizer.zero_grad()
        logits = model(input)
        loss = criterion(logits, target)

    ...

2.edge_decision

註解對應到上述的公式1~5。演算法對應到3.剪枝，特別的是剪枝完還會使用model.check_edges檢查已剪枝數量，以用來決定該層是否還需要剪枝(限制剪枝和運算量)。

參數：
args.use_history：用來決定要不要使用歷史資料。
args.warmup_dec_epoch：能當做預訓練(不做剪枝)。
args.decision_freq：剪枝頻率。
candidate_flags：節點是否剪枝的標記。
score：將評估的標準經過正規化[0,1]相乘。
selected_edge_idx：取得最大分數的索引(貪婪算法)。
selected_op_idx：取得selected_edge_idx運算層機率最大的索引(貪婪算法)，因為前面忽略non-zero層所以這裡index要+1轉回原本運算層的index。

def edge_decision(type, alphas, selected_idxs, candidate_flags, probs_history, epoch, model, args):
    mat = F.softmax(torch.stack(alphas, dim=0), dim=-1).detach()
    
    # Formula 1
    importance = torch.sum(mat[:, 1:], dim=-1)

    # Formula 2
    probs = mat[:, 1:] / importance[:, None]
    entropy = cate.Categorical(probs=probs).entropy() / math.log(probs.size()[1])


    if args.use_history: # SGAS Cri.2 
        # Formula 3
        histogram_inter = histogram_average(probs_history, probs)
        probs_history.append(probs)
        if (len(probs_history) > args.history_size):
            probs_history.pop(0)
        
        # Formula 5
        score = utils.normalize(importance) * utils.normalize(
            1 - entropy) * utils.normalize(histogram_inter)

    else: # SGAS Cri.1
        # Formula 4
        score = utils.normalize(importance) * utils.normalize(1 - entropy)


    if torch.sum(candidate_flags.int()) > 0 and \
            epoch >= args.warmup_dec_epoch and \
            (epoch - args.warmup_dec_epoch) % args.decision_freq == 0:
        masked_score = torch.min(score,(2 * candidate_flags.float() - 1) * np.inf)
        selected_edge_idx = torch.argmax(masked_score)
        selected_op_idx = torch.argmax(probs[selected_edge_idx]) + 1 # add 1 since none op
        selected_idxs[selected_edge_idx] = selected_op_idx

        candidate_flags[selected_edge_idx] = False
        alphas[selected_edge_idx].requires_grad = False
        if type == 'normal':
            reduction = False
        elif type == 'reduce':
            reduction = True
        else:
            raise Exception('Unknown Cell Type')
        candidate_flags, selected_idxs = model.check_edges(candidate_flags,selected_idxs,reduction=reduction)
        print(type + "_candidate_flags {}".format(candidate_flags))
        score_image(type, score, epoch)
        return True, selected_idxs, candidate_flags

    else:
        print(type + "_candidate_flags {}".format(candidate_flags))
        score_image(type, score, epoch)
        return False, selected_idxs, candidate_flags

5.　結論

SGAS在NAS當中訓練速度是相當快的，而這次只運行CNN，資料集使用Cifar-10和MNIST，但一般我們遇到的資料可能不是CNN，而SGAS也考慮的了這點，因此還能用於GCN等等上(其實滿多都能用在不同地方)，另外如果有時間會在打上一篇來講解如何用在Kaggle的鐵達尼號或房價預測，並且使用sklearn-AutoML來進行比較，感覺上AutoML在節省人力與實用性算是相當高的，希望未來有機會能夠在工作場所發揮。
有任何問題或筆誤歡迎留言

6.　程式碼

修改後原始碼：jupyter notebook code
修改後原始碼：Github
論文原始碼：SGAS Github

7.　參考文獻

[1] Li, G., Qian, G., Delgadillo, I.C., M¨uller, M., Thabet, A., Ghanem, B.: Sgas: Sequential greedy architecture search. In: Proceedings of the IEEE Conference on
Computer Vision and Pattern Recognition (2020).
[2] X. He, K. Zhao, and X. Chu, “Automl: A survey of the state-of-the-art,” arXiv preprint arXiv:1908.00709 (2019).
[3] K. He, X. Zhang, S. Ren, and J. Sun. Deep residual learning for image recognition. In CVPR, 2016.