這邊指的模型不只是最近很潮的機器學習或深度學習，而是廣泛指透過資料建立用來代表現實的抽象概念（白話來說就是一堆數學）。模型並不是資料本身，但好的模型會能表現資料展現的特質。就像鋼彈模型不是鋼彈，但會充滿真正鋼彈的細節。

(圖1: RX-78F00)

描述性模型

(來源：https://www.datavedas.com/descriptive-statistics/)

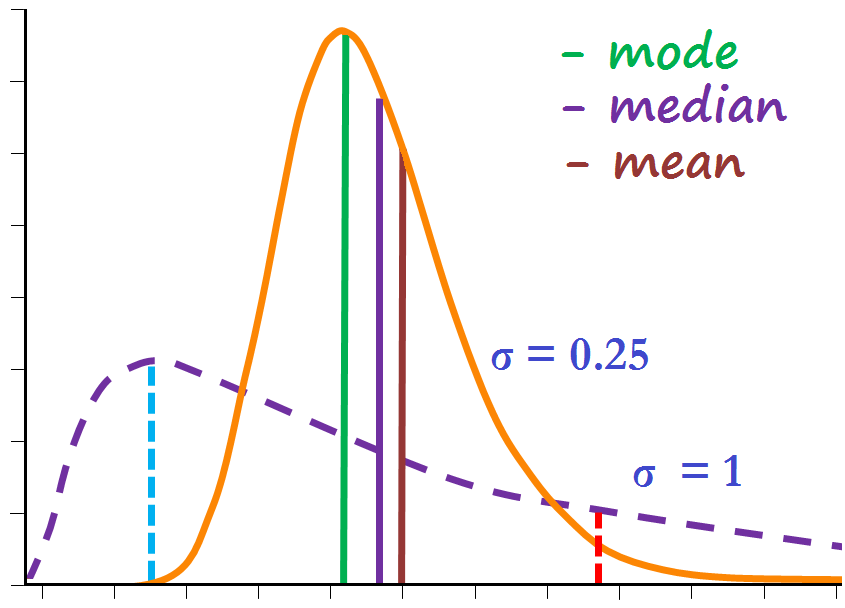
描述性模型重點在於用簡單的方式來解釋手上的資料。例如當你在自我介紹時，很容易就能講出自己的身高體重，但如果要描述一個班級甚至一個城市的人的身高體重，就沒辦法用這種方式，因此需要一些描述性的模型來幫助我們補捉個輪廓，例如常聽到的平均數、常態分配就屬於這類。

資料類型

不同類型的資料可以用的描述方式不同，在做分析之前一定要先辨識資料的類型。

• 類別型資料(Nominal): 只能數個數，但是不能直接進行數值運算，像是顏色、品牌、性別。
• 等序資料(Ordinal): 像是等第（A、B、C）、喜歡程度（1-5 分），數值之間可以比大小但是沒辦法運算的資料。
• 等距資料(Interval): 數值型資料，沒有絕對的零（例如溫度）。
• 等比資料(Ratio): 也是數值型資料，但有絕對的零（例如速度、距離等）。

集中趨勢

集中趨勢指的是資料往哪集中，如果數列是 [1, 2, 2, 3, 4, 5, 6]

• 眾數 - 相同資料最多的地方，也就是 2
• 中位數 - 資料由小大到排序後的中心點，也就是 3
• 平均數 - 資料的重心，數字加總後除以個數，等於 3.28

集中趨勢用來描述資料很方便，但也會喪失許多精準度，最常見的例子就是「台灣平均每個人有 1.1 個睪丸」。因此在使用上也需要注重集中趨勢的特性以及資料的脈絡才能避免誤用。

離散程度

離散趨勢和集中相反，描述的是資料散亂的程度。常用的像是：

• 全距: 很單純就是用最大值減去最小值，可以概括知道資料的狀況。
• 標準差: 自己看了，有點難文字描述 https://zh.wikipedia.org/zh-tw/%E6%A8%99%E6%BA%96%E5%B7%AE， 由於是個標準化的計算方式，所以不同單位的資料都可以用標準差來衡量離散程度。

分佈型態

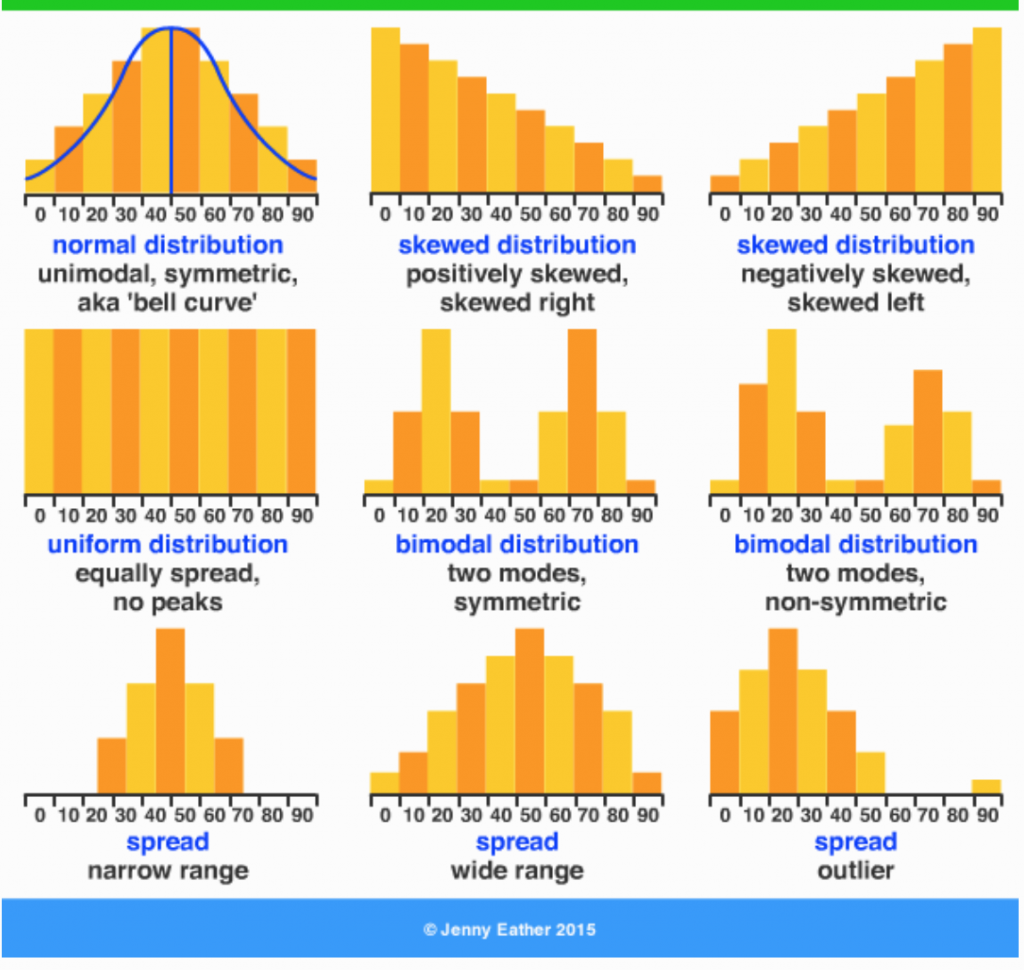
(https://jackrowansflightlogs.blogspot.com/2020/04/uniform-data-distribution.html)

通常資料實際上的長相不會是一兩個數字能夠完整描述的，像上圖這些資料集中和離散程度可能都差不多，但是樣貌天差地遠。

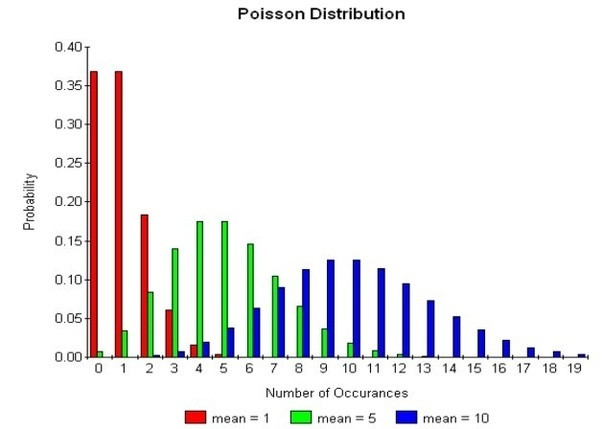
(https://www.quora.com/How-is-Poisson-distribution-the-limit-of-binomial-distribution)

由於資料分佈會有常見的模式，因此我們也會使用一些數學公式來描述資料分佈狀況（像上圖的 Possion 分佈）。而資料的分佈型態也會直接影響可以用的分類模型，像是下圖這種同心圓的資料分佈就不適合使用 K-Means 演算法。

探索型資料分析 EDA(Exploratory Data Analysis)

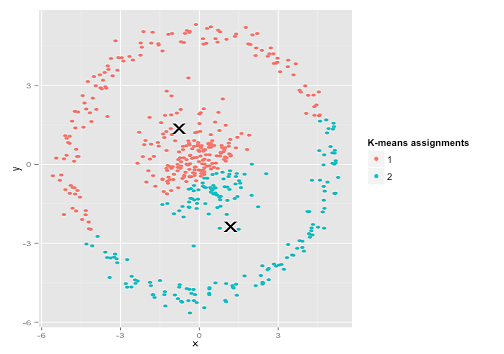
一般來說，在正式進資料分析或建模前都會透過這樣的探索型分析來了解資料的樣貌。由於資料量通常很多，沒有辦法一個一個檢查，因此會透過這篇介紹的描述性模型來將資料做摘要，方便分析人員可以更快瞭解資料的樣貌、找出資料異常。這裡分享一下我常用的起手式：

1. 為每個欄位進行描述統計，了解每個欄位的集中與分散狀況，抓出特別的 Outlier 和 Null 值。
2. 為每個欄位畫分佈圖，了解資料樣貌。
3. 將欄位畫交叉散佈圖，了解兩兩資料之間的關聯。
4. 以時間為 X 軸了解每個資料在時間上的變化。

(https://www.r-bloggers.com/2020/08/time-series-in-5-minutes-part-1-data-wrangling-and-rolling-calculations/)

References

https://wiki.mbalib.com/zh-tw/%E6%A8%A1%E5%9E%8B
https://www.sciencedirect.com/topics/computer-science/descriptive-model
https://towardsdatascience.com/exploratory-data-analysis-eda-a-practical-guide-and-template-for-structured-data-abfbf3ee3bd9