一、為何要做標準化

以最簡單的方式來說，一份資料中，不可能每個特徵的範圍都是一樣的，當我們需要拿兩筆特徵資料來做處理時，就必須讓他們的評比標準都相同才會準確。舉裡來說，研究所考試中有些科目是可以選考的，有些人選管理學、有些人選統計來考，但因為題目不一樣你不能直接拿兩筆資料的分數來排名。因此我們必須透過標準化的方法把兩筆資料的範圍變成相同，資料拿來比較才具有意義且公平。

二、標準化方法

1. 正規化

又稱最大最小化。可防止較大初始值域與較小初始值域屬性間互相比較的情況，以及權
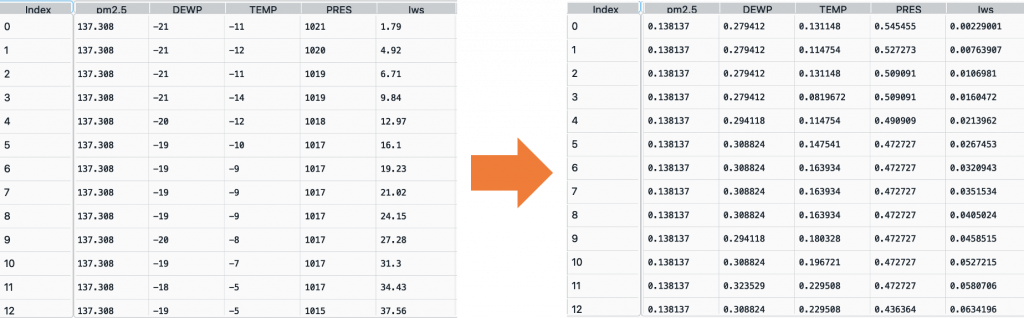
重過大的問題。將值壓縮到[0,1]之間。可以避免離群值影響資料。（如下圖）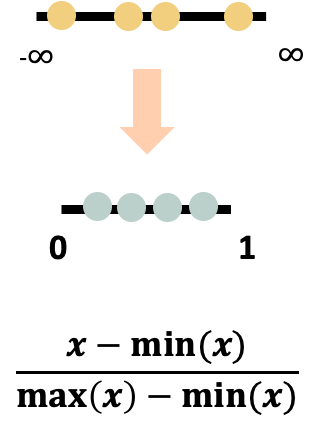

train=pd.read_csv("train.csv")
y=pd.DataFrame(train["pm2.5"])
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
y_train_scaled = scaler.fit_transform(y)
train_scaled = scaler_two.fit_transform(train)
train_scaled=pd.DataFrame(train_scaled,columns = ['month', 'day', 'hour', 'pm2.5', 'DEWP', 'TEMP', 'PRES', 'Iws', 'Is','Ir', 'cbwd_NE', 'cbwd_NW', 'cbwd_SE', 'cbwd_cv', 'year_2010',
'year_2011', 'year_2012', 'year_2013', 'year_2014'])

2. 標準化

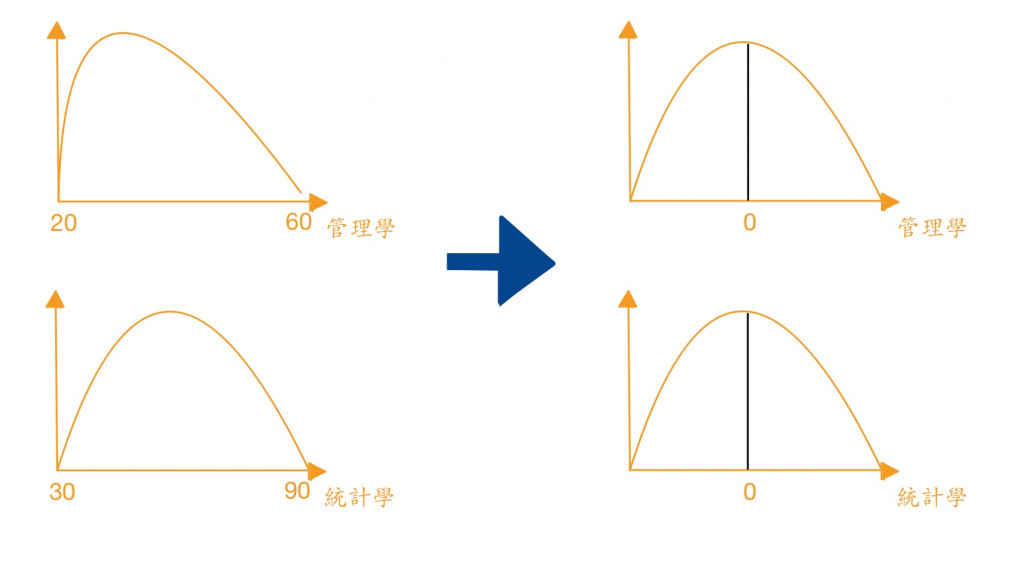
將不同的資料變成相同的標準值，以我剛才舉的例子來說，透過標準化，我們可以將資料變成平均值為0變異數為1的標準常態分配，而轉換過後我們就可以拿來做比較了。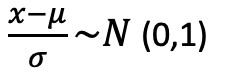

def normalize(x_train, x_test, method = 'StandardScaler'):
    '''
    method = 'StandardScaler', 'PowerTransformer', 'MinMaxScaler'
    '''    
    if method == 'StandardScaler':
        normalize_function = preprocessing.StandardScaler()
    if method == 'PowerTransformer':
        normalize_function = preprocessing.PowerTransformer(method='yeo-johnson', standardize=True) # yeo-johnson, box-cox     
    if method == 'MinMaxScaler':
        normalize_function = preprocessing.MinMaxScaler()
    
    features = x_train.columns
    for feature in features:
        reshape = np.array(x_train[feature]).reshape(-1, 1)
        x_train[feature] = normalize_function.fit_transform(reshape)

        reshape = np.array(x_test[feature]).reshape(-1, 1)
        x_test[feature] = normalize_function.transform(reshape)
    
    return x_train, x_test

right_ratio_x_train, right_ratio_x_test = normalize(right_ratio_x_train, right_ratio_x_test)

3. log轉換

當資料為常態分配的時候，他的範圍介於-∞<x<∞之間，但生活中很少有資料介於這個範圍。因此我們將資料經過log轉換後，資料的範圍就會介於0<x<∞之間了。

log_df = np.log1p(df["你要轉換的資料名稱"])

三、為何要做降維

在使用一些監督式學習的模型時，丟入訓練的資料維度對結果有很大的影響，當丟入訓練的資料的維度較大時，我們需要用一些方法來降低數據維度，雖然不能保證說用這個方法就一定能讓結果變好，但在做資料分析時就要有勇於嘗試的態度，才有機會找到最適合這筆資料的處理方法。

四、降維的方法

1. LDA

是一種用來確定“最佳”變量集，識別一個新的軸，並用來分類

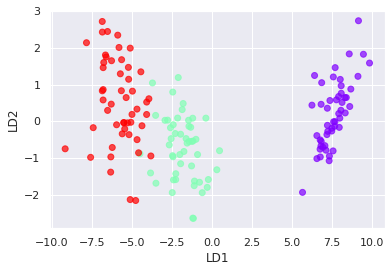
用內建資料集資料鳶尾花實作

import numpy as np
import pandas as pd
from sklearn import datasets
#載入資料集
iris = datasets.load_iris()
iris.keys()
X = pd.DataFrame(iris.data, columns=iris.feature_names)
y = iris.target
#使用LDA將資料變成二維
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
lda = LinearDiscriminantAnalysis(n_components=2)#將資料縮減成兩個維度
X_lda = lda.fit_transform(X, y)

lda.explained_variance_ratio_

2. PCA(主成分分析)

主成份分析的主要目的為，用較少的變數解釋原始資料中大部分的變異，並將原本相關性很高的變數轉換成相互獨立的變數，降低變數的維度。

底下我們用內建資料集資料鳶尾花實作

import numpy as np
import pandas as pd
from sklearn import datasets
#載入資料集
iris = datasets.load_iris()
iris.keys()
X = pd.DataFrame(iris.data, columns=iris.feature_names)
y = iris.target
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
X_pca = pca.fit_transform(X_train)
plt.xlabel('PC1')
plt.ylabel('PC2')
plt.scatter(
    X_pca[:,0],
    X_pca[:,1],
    c=y_train,
    cmap='rainbow',
    alpha=0.7,
    edgecolors='b')

3. LDA和PCA差別

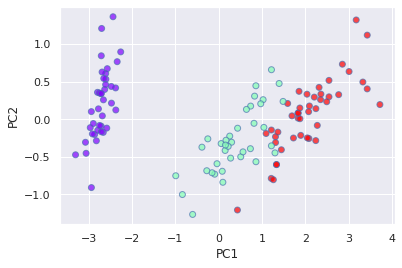
PCA 是一種非監督式算法，其目標是找到資料集中的主成分之間最大的變異數。
LDA 是一種監督式的半別方法，將資料投影到軸上。可以形成特徵內彼此之間最小差異，與不同特徵最大差異。

五、結論

今天所介紹的這些方法參雜了很多數學概念，若讀者們有興趣可以自行到網路上去收尋相關的數學知識來看，對知識的了解越深越廣，在資料分析這條路上才能走得更加長久喔～