機器學習可以分成監督式學習與非監督式學習,這部分我們在第四天有稍微提到過,這邊就不多做說明了,今天我們將介紹這兩類的問題分別適合用什麼模型來做處理。
羅吉斯回歸是一種分類演算法,其原理為找到一條線將資料盡可能的區隔出來,可以處理二元分類的問題。
from sklearn import datasets
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import mean_squared_error, accuracy_score
#載入資料集
iris = datasets.load_iris()
#資料整理
x = pd.DataFrame(iris['data'], columns=iris['feature_names'])
y = pd.DataFrame(iris['target'], columns=['target'])
iris_data = pd.concat([x,y], axis=1)#將資料合併
print(iris_data)
#透過兩個特徵來進行分類
iris_data = iris_data[['sepal length (cm)','petal length (cm)','target']]
print(iris_data)
#這邊分成兩個類別 (山鳶尾、變色鳶尾)
iris_data = iris_data[iris_data['target'].isin([0,1])]
iris_data
X = iris_data[['sepal length (cm)','petal length (cm)']]
y = iris_data[['target']]
#切分訓練集以及測試集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=0)
print('len X_train:',len(X_train),'len X_test:',len(X_test))
#將資料常態分布化,平均值會變為0, 標準差變為1,使離群值影響降低
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)
#使用上面整理好切割好的資料做訓練
lr = LogisticRegression()
model = lr.fit(X_train_std,y_train['target'].values)
#%%分類預測結果
predict = model.predict(X_test_std)
print("predict label:",predict)
#創建顏色庫
markers = ('s', 'x')
colors = ('orange', 'darkblue')
cmap = ListedColormap(colors[:len(np.unique(y))])
#將分類的區塊視覺化
x1_min, x1_max = X_train_std[:, 0].min()-1, X_train_std[:, 0].max()+1 # 特徵1最小值與最大值
x2_min, x2_max = X_train_std[:, 1].min()-1, X_train_std[:, 1].max()+1 # 特徵2最小值與最大值
xx1, xx2 = np.meshgrid(np.arange(x1_min, x1_max, 0.01),np.arange(x2_min, x2_max, 0.01)) # 將數據變成m*n矩陣:(m根據前面array長度,n根據後面array長度);0.01為contourf的精度
Z = lr.predict(np.array([xx1.ravel(), xx2.ravel()]).T) #ravel將矩陣拉平成一維
Z = Z.reshape(xx1.shape)
plt.figure(figsize=(12,8))
plt.contourf(xx1, xx2, Z, alpha=0.4, cmap=cmap)
plt.xlim(xx1.min(), xx1.max())
plt.ylim(xx2.min(), xx2.max()) #Y軸範圍
#畫test資料點位置
y_test_n=np.array(y_test.values)#將label data變成跟特徵的類型一樣以利後續畫圖
plt.scatter(X_test_std[:,0], X_test_std[:,1],alpha=0.6,c = y_test_n,edgecolor='black',marker='s')
plt.xlabel('sepal length (cm) [standardized]',size=20)
plt.ylabel('petal width [standardized]',size=20)
plt.show()
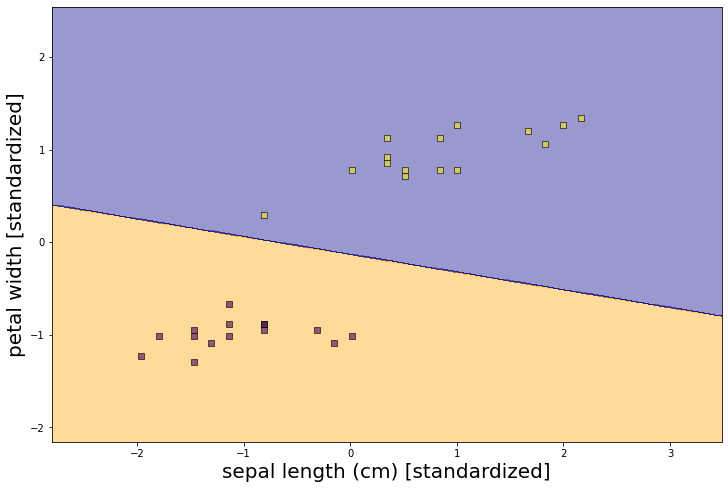
從上圖可以看到模型幫助我們找到一條線將資料分成兩類。
透過一系列的是非問題,幫助我們將資料進行切分
訊息增益:
用來選特徵的,決策樹模型會用特徵切分資料,該選用哪個特徵來切分就是由訊息增益的大小決定的。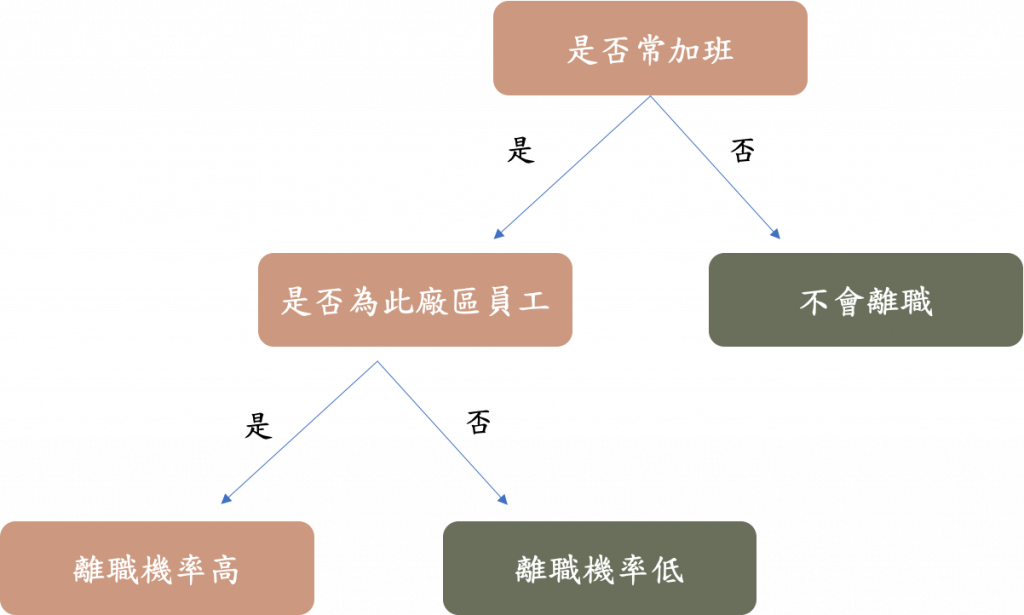
clf = tree.DecisionTreeClassifier()
clf = clf.fit(df_X, df_Y)
隨機森林就是將多個決策樹集合而成,為的就是改善決策樹容易overfitting的問題,而隨機森林也是一種集成學習。
集成 (Ensemble) 就是將多個模型的結果組合在一起,透過投票或是加權的方式得到最終結果,如下圖所示: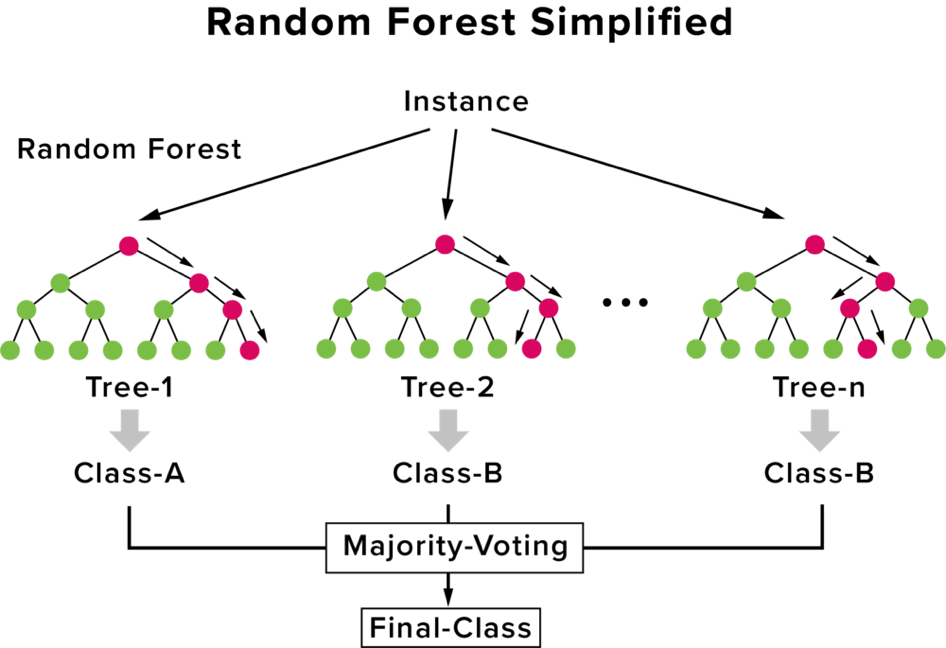
圖片來源:機器學習百日馬拉松Day43隨機森林 (Random Forest) 介紹
from sklearn.ensemble import RandomForestClassifier
rfc=RandomForestClassifier(n_estimators=100)
rfc_model=rfc.fit(df_X,y)
pred_test = rfc_model.predict(data_test)
XGBoost是boosting算法的其中一種,Boosting算法的概念是將許多弱分類器集成在一起,形成一個強分類器。有興趣的可以參考原文網址:https://kknews.cc/news/grejk5m.html
from xgboost import XGBClassifier
xgbc=XGBClassifier()
xgbc_model=xgbc.fit(df_X,y)
pred_test = xgbc_model.predict(data_test)
SVM = SVC()
svc_model = SVM.fit(X_train_std,y_train)
線性迴歸的目的在於找到一條可以擬合數據的線,使預測值與真實值之間的殘差越小越好,通常可作為 baseline 模型作為參考點。
# 讀取糖尿病資料集
diabetes = datasets.load_diabetes()
x = pd.DataFrame(diabetes['data'],columns=diabetes['feature_names'])
y = pd.DataFrame(diabetes['target'],columns=['target'])
diabetes_data = pd.concat([x,y], axis=1)#將資料合併
diabetes_data
# 取用bmi的特徵
X = np.array(diabetes_data.iloc[:,2:3])
y = np.array(diabetes_data.iloc[:,10:11])
print("Feature shape:", X.shape,"target shape:",y.shape)
#切資料
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.1, random_state=0)
print('len X_train:',len(X_train),'len X_test:',len(X_test))
# 建立一個線性迴歸模型
reg = LinearRegression()
# 將訓練資料丟進去模型訓練
reg_model = reg.fit(X_train, y_train)
# 將測試資料丟進模型得到預測結果
y_pred = reg_model.predict(X_test)
# 迴歸模型的係數與截距
print('coefficients:',reg.coef_)
print('intercept: ',reg.intercept_)
# 預測值與實際值的差距,使用 MSE
print("Mean squared error: %.2f"% mean_squared_error(y_test, y_pred))
# 看模型的準確度
print("R square: %.2f"%r2_score(y_test,y_pred))
#模型效果視覺化
plt.scatter(X_test,y_test,color='black')
plt.plot(X_test, y_pred, color='blue', linewidth=3)
plt.xlabel('bmi',size=20)
plt.ylabel('target',size=20)
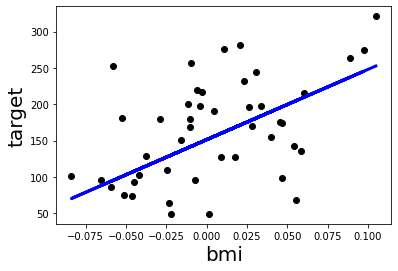
由上圖可以看到黑色的點點是我們的預測值
# Modeling
rf = RandomForestRegressor(n_estimators = 400, min_samples_leaf=0.12, random_state=123)
#Fitting Random Forest model
rf.fit(X_train, Y_train)
#Predicting using the Random Forest model
Y_pred = rf.predict(X_test)
Y_pred = pd.DataFrame(Y_pred).astype('int')
#Evaluate
print('Mean Absolute Error(MAE):', metrics.mean_absolute_error(Y_test, Y_pred))
print('Mean Squared Error(MSE):', metrics.mean_squared_error(Y_test, Y_pred))
print('Root Mean Squared Error(RMSE):', np.sqrt(metrics.mean_squared_error(Y_test, Y_pred)))
import xgboost
xgb=xgboost.XGBRegressor()
xgb.fit(X_train, Y_train)
xgb_pred = xgb.predict(X_test)
SVM = SVR()
svr_model = SVM.fit(X_train_std,y_train)
我們利用內建資料集來實作
import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from sklearn.datasets import make_blobs #用於生成聚類資料集
from sklearn.cluster import KMeans
#生成
x, y = make_blobs(n_samples=300, centers=4, cluster_std=3, random_state=0) #cluster_std = The standard deviation of the clusters
df = pd.DataFrame({'x':[x],'y':[y]}) #feature 2 dim ,y=label
plt.scatter(x[:,0], x[:,1],c=y)
x = pd.DataFrame(x,columns=['x1','x2'])
y = pd.DataFrame(y,columns=['y'])
from sklearn.cluster import KMeans
n_clusters=4
kmean = KMeans(n_clusters=n_clusters, random_state=0)
kmean.fit(x)
pred_y = kmean.predict(x)
plt.scatter(x=x.iloc[:,0], y=x.iloc[:,1],c=pred_y)
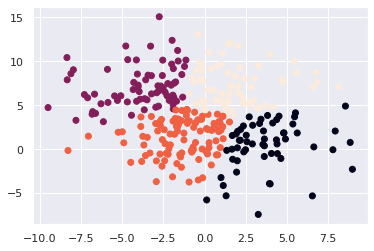
我們設定參數k為四群,而從畫出來的圖可以看到特徵被有效的分成四群。
看到上述的這些模型,是不是覺得頭昏腦脹呢?這還只是一小部分而已,之後在這個領域接觸的越深,所碰到的資料也會越複雜,甚至還可能需要自己寫出一個模型,不過對於初學者來說,能夠了解這些模型的原理並知道如何使用它,就可以幫助我們完成一些專案了。
