想要利用接下來的幾篇文章把tree-based的模型稍微介紹一下，所有的tree-based模型基本上都是從decision tree發展來的，他最大的優勢在於：

1. 過程透明好解釋：在報告給老闆的時候樹狀圖一拿出來非常簡單明瞭！
2. 可以解決regression problems 與 classification problems：也就是你今天想要預測房價（數值問題）或是腫瘤是良性還是惡性（Yes/No），decision tree都做得到。

Decision tree 原理

Decision tree最終會產生樹狀圖，每一個分支都是一個yes/no的問題，而主要的運算是在決定這些分支怎麼切來使最終的預測結果準確率最高，下圖是一個以美國各州收入.教育程度及種族多樣性來預測政治傾向的舉例，那這三個變數要怎麼選擇呢？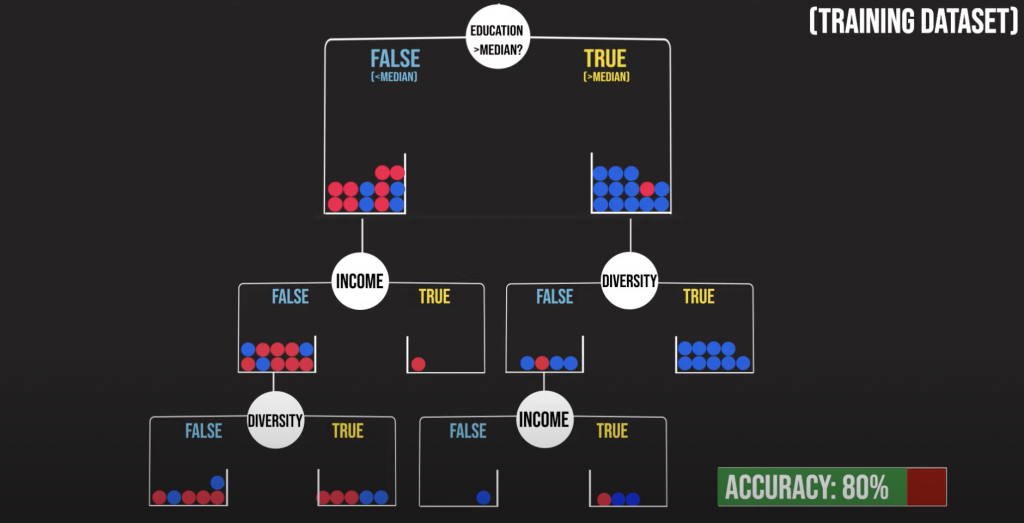

information gain

decision tree會依照“information gain”來決定，所謂“information gain”就是該變數讓你多獲得的資訊以利於正確判斷出結果的程度，從下方最左邊的圖，我們可以看出若一個州的教育程度大於所有州的中位數，那該州會有很大的機率是民主黨（藍球），而若小於所有州的中位數，則該州為共和黨（紅球）的機率為民主黨（藍球）的兩倍；反觀種族多樣性的變數，在白人比例大於中位數的情形下，的確會有較大的機率是藍球，但若是白人比例小於中位數，基本上會出現無法判斷的情況（紅藍球各半），所以相較之下教育程度能給我們的資訊量較大，也就會先選擇教育程度當成我們的首要分支。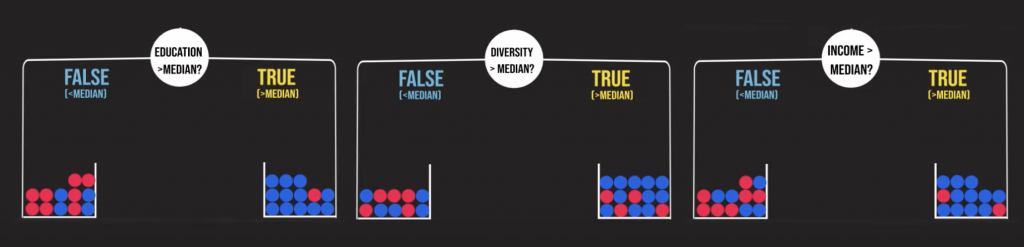

impurity

這裡會有另一個詞稱為“impurity”，可以把它想像成每個籃子裡紅藍球的混雜程度，如果箱子裡都是同一種顏色的球，那impurity 就會接近0，若籃子裡不同顏色的球佔了差不多的比例，那impurity就會來到最大值。其實decision tree的中心原則就是把總體的impurity降到最低。

在建構好樹狀圖之後，基本上就是讓你的新資料從頭開始走分支，抵達最後的盒子後，如果是分類問題就採用投票的方式（紅球多就說預測他是紅色，籃球多就預測他是藍色），如果是預測數值就採用平均數來當預測值。

另外decision tree非常容易有overfitting的情況發生，詳細的內容在之後寫python應用的時候會一起提到！
To be continue ʘ ͜ʖ ʘ

reference:
https://www.youtube.com/watch?v=zs6yHVtxyv8