話說小弟推出孔子和耶穌都講過「初戀無限美」的「刻骨銘心初戀金銀情侶套餐」時，竟被中國廚藝學院105屆畢業生唐牛吐槽根本是街邊「雜碎麵」，還說我煮的麵「咖哩魚蛋沒魚味，咖哩又不入味，失敗！豬皮煮得太爛，沒咬頭，失敗！豬紅鬆撲撲，一夾就散，失敗！蘿蔔沒挑過都是筋，失敗中的失敗！最離譜的就是這些大腸，完全沒洗乾淨，還有塊屎，你有沒有攪錯呀？」，最後還秀了一手，讓我重新見識到如何用「心」煮出一碗頂級好吃的雜碎麵，真是情何以堪。

現在市面上許多教AI應用的補習班或老師總是為了讓學生速成、有感，因此多半只教馬上看的到成果的內容和按圖施工的步驟，而少教枯燥乏味的原理，導致學生離開老師現成的範例後卻無法完成自己應用或搞不懂如何調校的冏境，就像只會用調理包是煮不出一碗內容豐富、刀工精湛且口味有層次的雜碎麵。

為了讓大家後續自行開發MCU程式碼（包括全部自刻或使用Arm Mbed作業系統加上CMSIS函式庫）或使用tinyML現成開發平台（如TensorFlow Lite for Microcontroller, Edge Impulse, cAInvas, SensiML等）時都能更加游刃有餘。

接下來的章節會依序將MCU、AI及tinyML獨立及交集部份逐一分篇說明。大家可能要花個幾天了解一下基礎知識，以免後續實際操作tinyML時，就像新手開自排車，只知踩油門、剎車和轉方向盤就能把車開上路，但搞不懂如何讓車子能開的更順暢，更不容易翻車。

在[Day 02] Fig. 2-1 中已清楚描繪出人工智慧(AI)、機器學習(ML)、神經網路（NN）和深度學習(DL)的層級架構。這裡要先了解，tinyML的ML實際上指的不單純是機器學習或神經網路或深度學習，而是泛指在指定時間內能計算推論出結果的算法，其結果亦包含了耗能，當計算平行度越高或時間越長時就會導致耗能越大，因此更清楚了解模型運作模式就有機會創作出更低耗能、更高效率的Edge AI應用了。

在開始學習應用tinyML之前，我們還是得先了解何謂「神經網路」和「深度學習」，再了解如何「訓練」及「推論」模型（或稱為網路），才不會後續操作時不知如何下手。話說1950年代，科學家們想讓計算機也能像人類一樣擁有學習及思考能力，於是仿效了大腦神經元及神經突觸相互連結的結構，創造出感知機(Perceptron)。如下圖(Fig. 4-1)左方所示，每個神經元可以有多個輸入值(Xn)，每個輸入可以有不同權重值(Weight)(Wn)，最後加總所有乘積輸出，就成了一個神經元基本單元。

當有很多個神經元時就能組成網路（或稱為模型），如Fig. 4-1右側所示。最簡單的人工神經網路(Artificial Neural Network, ANN或簡稱NN)，通常只有三層，輸入層(Input Layer)、隱藏層(Hidden Layer)和輸出層(Output Layer)。每一層的神經元個數不限，原則上採全連結(Full Connected)方式，就是相鄰兩層的所有節點必須互連。如圖所示，輸入層三個、隱藏層三個及輸出層兩個神經元時，需要的權重值（每條連線）就有(3 x 3) + (3 x 2) = 15組，若以Float數值(4 Byte)來表示，則需要15 x 4 = 60 Byte來儲存。當隱藏層的數量增加時，其連結數（權重值）也會瞬大幅提升。

除此之外，通常還會在神經元加上一個偏置量(Bias)及在輸出端加上一個可微分的非線性函數，稱為「激勵函數(Activation Function)」，經過轉換後通常會使輸出值限縮在0 ~ 1(如Sigmoid)或-1 ~ +1(如Hyperbolic Tangent, tanh)之間，相當於變相將下一級輸入的值進行正規化。關於模型訓練問題就留待後面章節再進行說明。

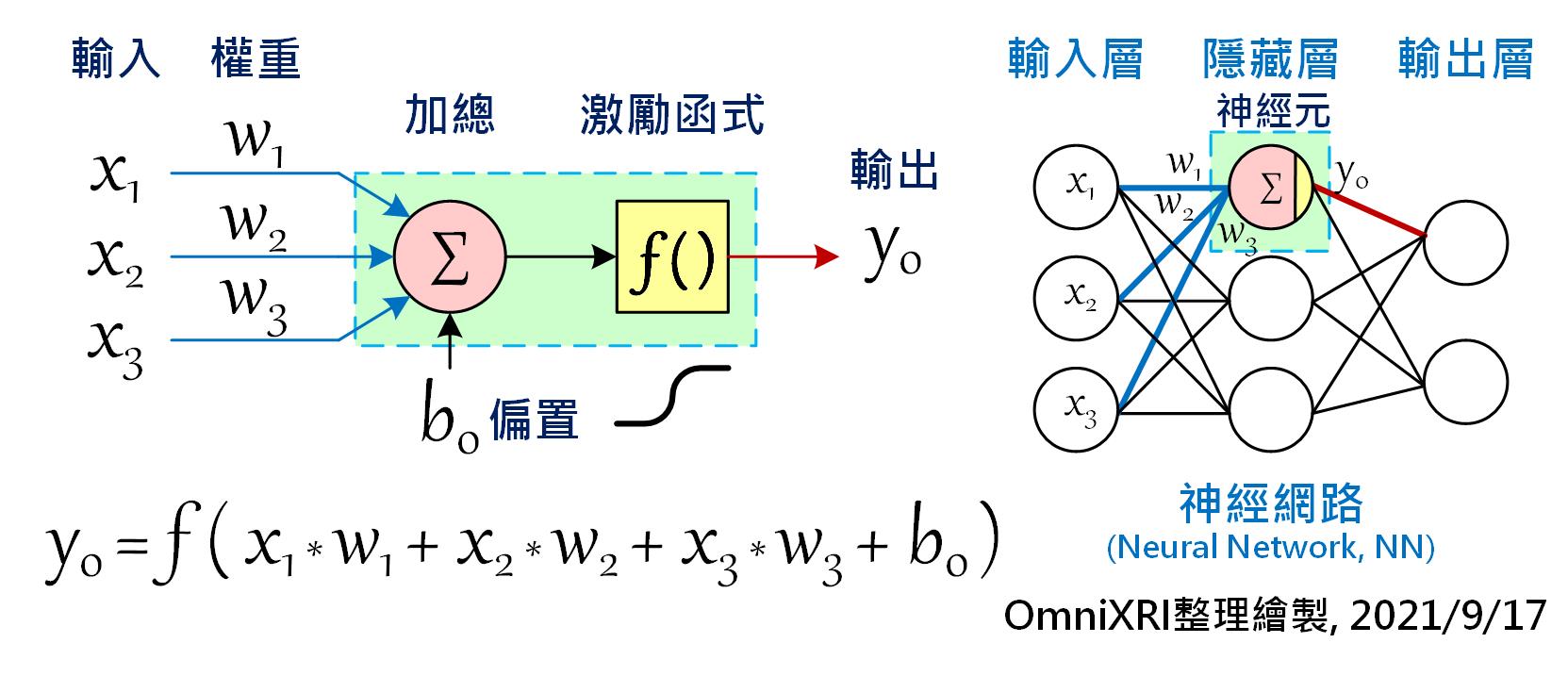
Fig. 4-1 神經元與神經網路。（OmniXRI整理繪製, 2021/9/17)

以下為C語言格式參考示意程式，當然這段程式很容移植到Arm Cortex-M的MCU上。透過程式碼也可初步了解到，一個有三個輸入值，三個權重值、一個偏置量及一個輸出值的神經元至少需要佔用4個Float共16 Byte的程式碼區，和5個Float共20 Byte的隨機記憶體(SRAM)來供計算時使用。因為通常訓練好的權重值和偏置量是不會變動的，放到程式碼區即可，而輸入和最後的輸出值會一直變動所以要放到SRAM中。而除了輸入值、權重值及偏置量外，程式碼及SRAM最後會佔用多少則和程式碼寫法及編譯器設定有關，這裡就暫不分析，待後續完整範例介紹時再行說明。

// 以常數值方式宣告已訓練完成的權重值及偏置量
const float w[3] = {7.3, 0.6, 2.6}; // 權重值
const float b0 = 2.1; // 偏置量
  
// Sigmoid激勵函式 (輸出 0.0 ~ 1.0)
sigmoid(float val)
{
 return(1 / (1 + exp(val)));
}

// 主程式，計算基本神經元輸出
main() 
{  
  float x[3] = {1,2,3}; // 輸入值
  float y0 = 0.0; // 輸出值
  float sum = 0.0; // 加總值

  // 加總所有輸入乘權重值
  for(int n=0, n<3; n++){
    sum += (x[n] * w[n]);
  }
  
  sum += b0; // 加上偏置量
  
  y0 = sigmoid(sum); // 以sigmoid激勵函式作為輸出轉換
}

ps. 為讓文章更活潑傳達硬梆梆的技術內容，所以引用了經典電影「食神」的橋段，希望小弟戲劇性的二創不會引起電影公司的不悅，在此對星爺及電影公司致上崇高的敬意，敬請見諒。