遞迴(Recursion)的概念是將一個大的問題,分割成許多小問題去解決。而從程式設計角度來看,函式不單只能被其他函式呼叫,也能被它自己呼叫,也就是在一個函式當中呼叫它自己,即為遞回函式(Recursive Function)。
例如:
要做一個5的階乘: 5!
5 x 4 x 3 x 2 x 1
def factorial(n):
if n == 1:
return 1
else:
return (n * factorial(n - 1))
print(factorial(5))#120
執行過程為下圖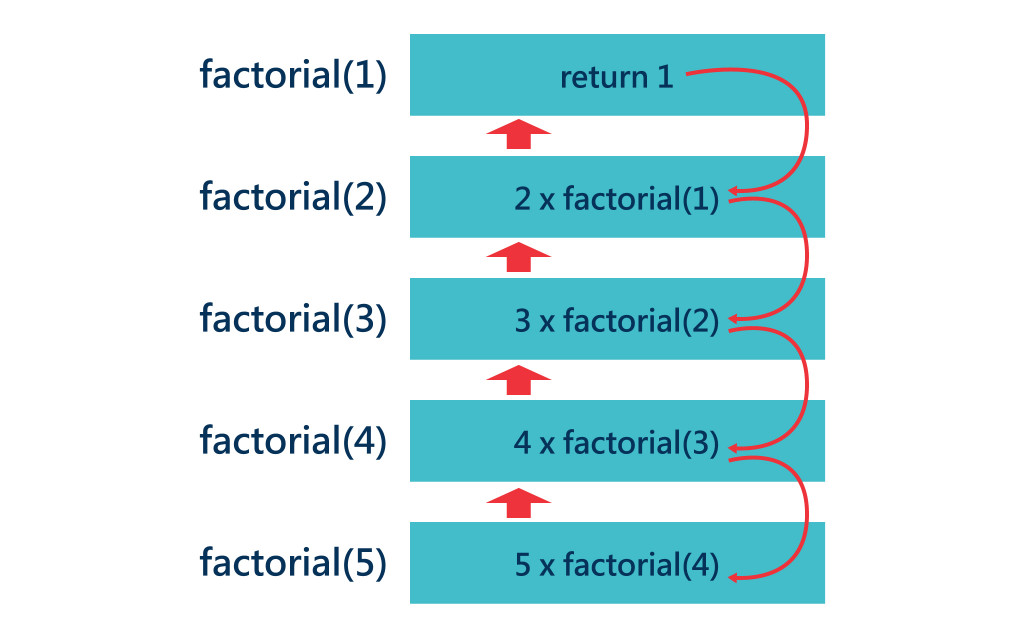
而遞回函式通常需要有兩項條件,一項是重複執行它自己,另一項則是跳出執行的出口,避免造成無窮迴圈。
能夠使用遞回函式,是因為函式堆疊(Stack)的特性,當函式呼叫另一個函式時,需等候裡面的函式執行完,才會繼續回來執行自己的函式內容,應用到堆疊(Stack)資料結構後進先出(LIFO)的概念。
堆疊的介紹可以參考此篇。
def first():
print('1')
last()
print('2')
def last():
print('3')
print(first()) #1>3>2
又稱費氏數列,是最有名的遞迴例子,裡面隱藏了黃金比例法則,詳細介紹如下影片:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, ...
第0項值是0,第1項值是1,其他值會等於本身前兩項的值相加,因此公式可以定義為:
F(0) = 0
F(1) = 1
F(n ) = F( n-1 ) + F( n-2 )
def fibonacci(n):
if n<1:
return 0
elif n==1:
return 1
else:
return fibonacci(n-1)+fibonacci(n-2)
print(fibonacci(5)) #5
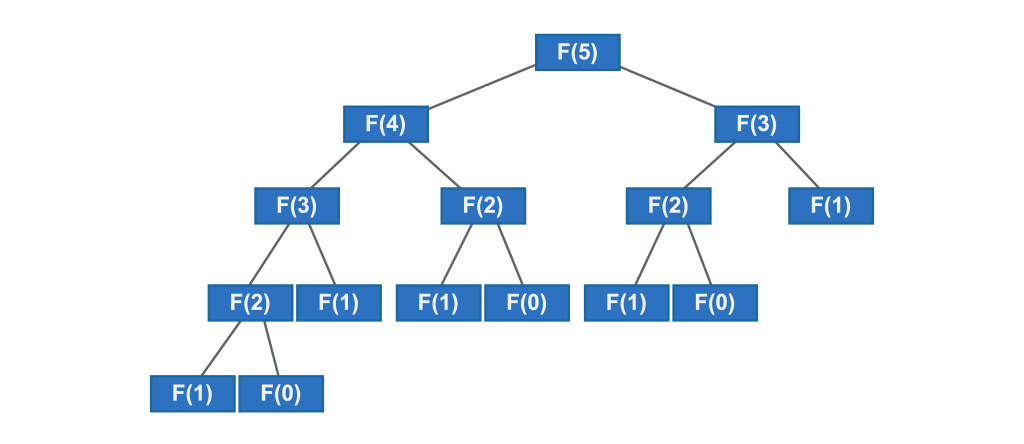
之所以先在這邊提到遞迴,是因為後面有許多實作會應用到遞回函式。
