之前在遞迴的篇章有介紹過費波那契數列，是使用遞迴的方式實作，但是從下面遞迴的樹狀圖來看，會發現有很多重複的節點，遞迴的深度越深，重複計算的節點也就越多，甚至會出現RecursionError的情況，而這樣的時間複雜度為O(2^n)。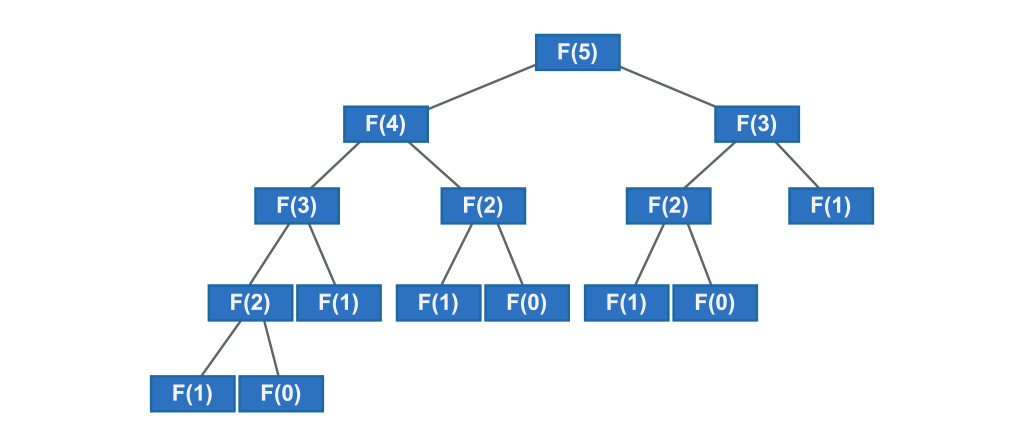

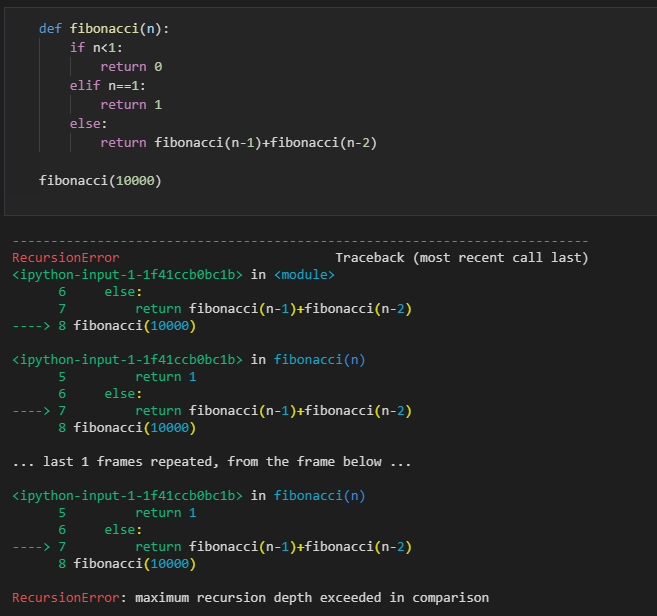
因此可以將會重複計算的部分暫存起來，避免重覆計算來增加處理效能。

def fibonacci(n):
    if n == 0 or n == 1:
        return n
    seq = [0 for _ in range(n + 1)]
    seq[0] = 0
    seq[1] = 1
    for i in range(2, n + 1):
      seq[i] = seq[i-1] + seq[i-2]
    return seq[n]

fibonacci(8)#21

• 建立一個seq列表
• seq[i]為F(i)的值，可以說seq[i] = seq[i-1] + seq[i-2]
• 把seq[0]為0、seq[1]為1
• 用迴圈計算i=2到n+1時，得出seq[i]的結果，儲存於seq列表中被使用
• 最後算出來的seq[n]，就是F(n)的值

透過上面的方式，可以發現真正被計算到的只剩下橘色部分，藍色框為已經被儲存在seq列表中，不需要重複計算，時間複雜度變為O(n)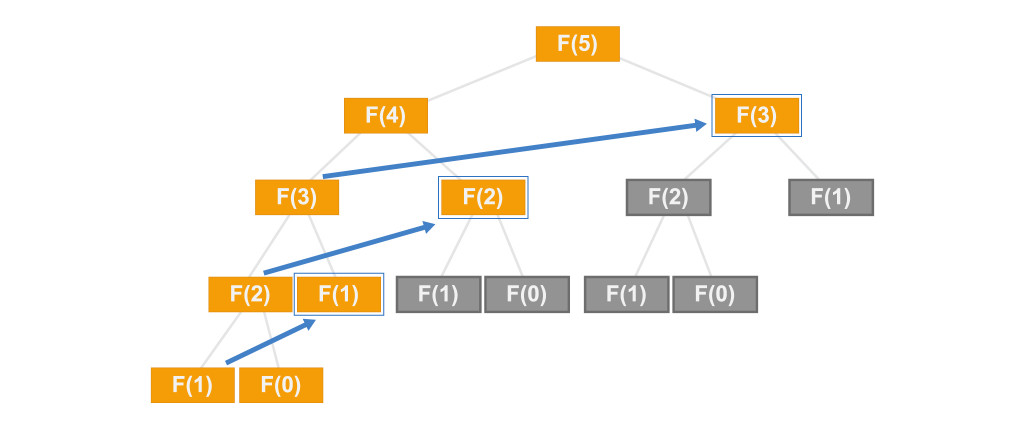

根據上述方式，空間複雜度為O(n)，但還可以有更進階的方式來節省空間。

def fibonacci(n):
    if n == 0 or n == 1:
        return n
    a = 0
    b = 1
    for i in range(2, n+1):
        c = a + b
        a = b
        b = c
    return b

fibonacci(8)#21

• 開始的前兩項a與b，為0與1
• 後一項c是前兩項的加總
• 只需要對a和b不斷重新賦值

空間複雜度就能從原本的O(n)變成O(1)。