深度優先搜尋(Depth-First Search,DFS)與廣度優先搜尋(Breadth-First Search, BFS)，是可以用來走訪或搜尋樹節點與圖頂點的演算法，先前介紹的二元樹走訪就是使用上述方法走訪各節點，這邊以圖結構來介紹。

樹的走訪可以參考此篇。

下面相鄰串列構成的圖來示範搜尋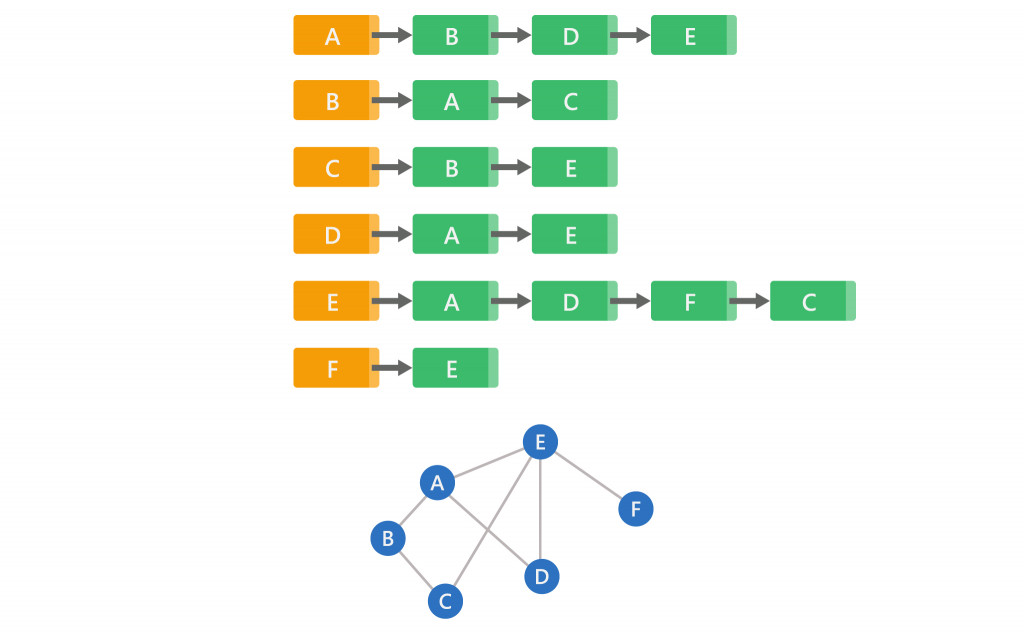

圖的介紹可以參考此篇。

深度優先搜尋DFS

先選定一個頂點開始走訪，接著從此頂點相鄰未被走過的頂點中，擇一走訪標示為記錄點，以此類推，不斷從新記錄點的相鄰未被走過頂點中尋找。
若新紀錄點的相鄰頂點都被走過，則退回前一個紀錄點，繼續從未被走過頂點中尋找。

深度優先可以利用堆疊(Stack)的方式來處理。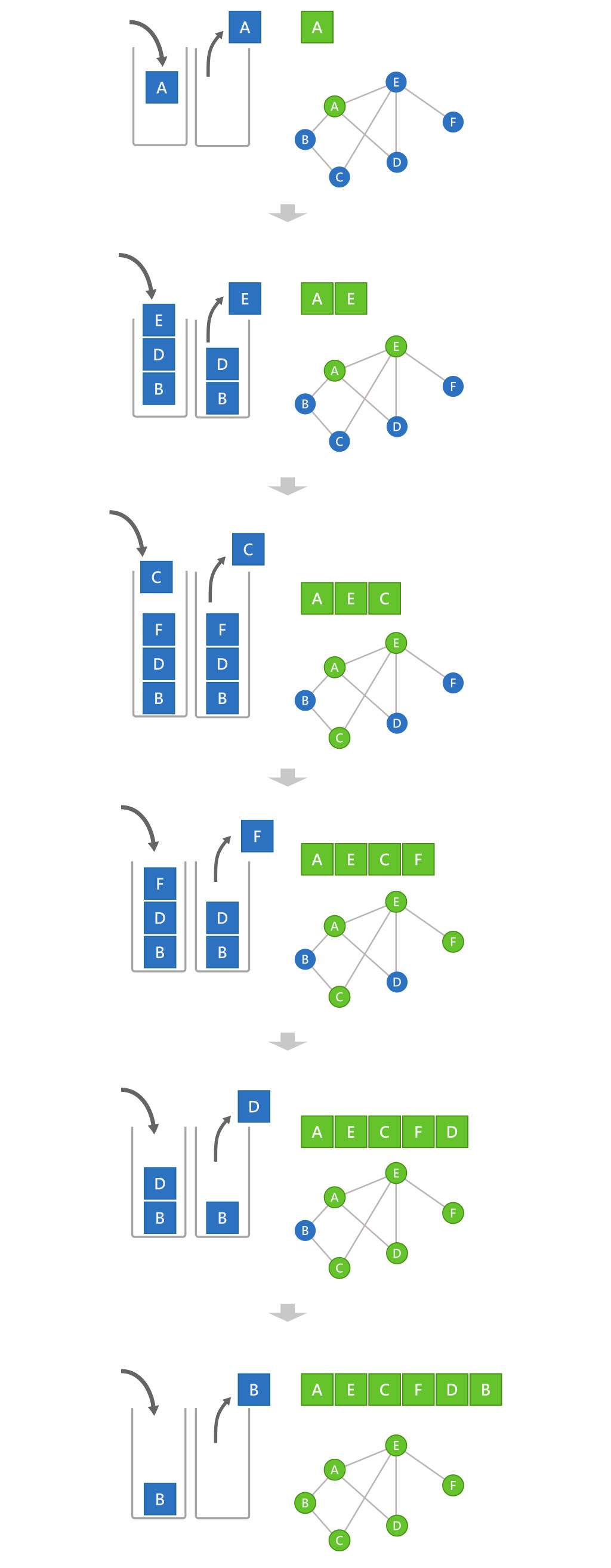

堆疊的介紹可以參考此篇。

廣度優先搜尋BFS

先選定一個頂點開始走訪，逐一走過此頂點相鄰未被走過的頂點，若相鄰頂點都被走過，再從走訪過的頂點中擇一為新記錄點，逐一走過新記錄點相鄰未被走過的頂點，以此類推。

廣度優先可以利用佇列(Queue)的方式來處理。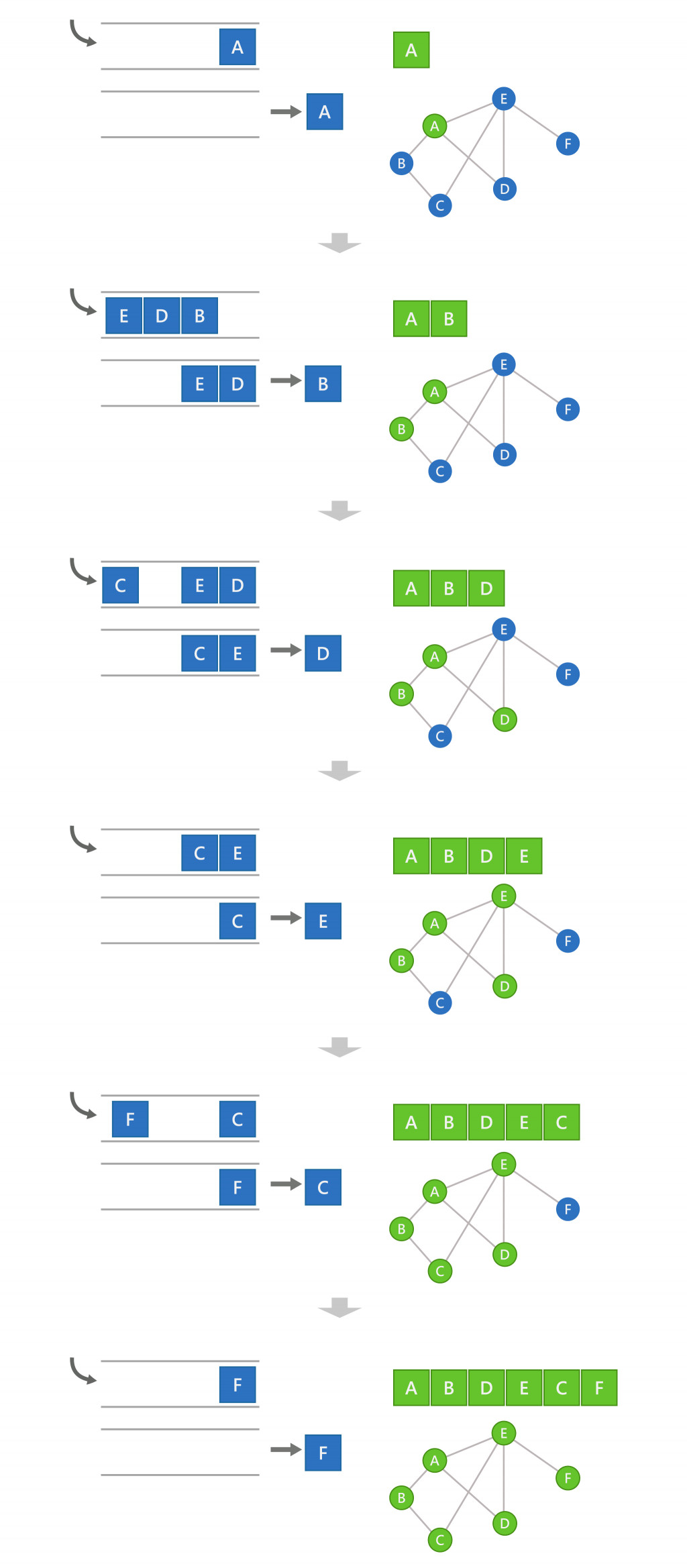

佇列的介紹可以參考此篇。

JavaScript

class Graph {
  constructor() {
    this.adjacencyList = {}
  }

	//新增頂點
  addVertex(vertex) {
    if (!this.adjacencyList[vertex]) {
     	this.adjacencyList[vertex] = []
    } else {
      return '頂點已存在';
    }
  }
  
  //新增邊
  addEdge(vertex1, vertex2) {
    if (this.adjacencyList[vertex1]) {
      if (this.adjacencyList[vertex2]){
        this.adjacencyList[vertex1].push(vertex2)
        this.adjacencyList[vertex2].push(vertex1)
      }else {
        return '第二項頂點不存在';
      }
    } else {
      return '第一項頂點不存在';
    }
  }
  
  //刪除頂點
  removeVertex(vertex) {
    if (this.adjacencyList[vertex]) {
     	this.adjacencyList[vertex].forEach(function(item) {
        this.removeEdge(vertex, item)
        delete this.adjacencyList[vertex]
      });
    } else {
      return '此頂點已不存在';
    }
  }
  
  //刪除邊
  removeEdge(vertex1, vertex2) {
    if (this.adjacencyList[vertex1]) {
      if (this.adjacencyList[vertex2]){
        this.adjacencyList[vertex1] = this.adjacencyList[vertex1].filter(
        	(vertex) => vertex !== vertex2
        )
        this.adjacencyList[vertex2] = this.adjacencyList[vertex2].filter(
        	(vertex) => vertex !== vertex1
        )
      }else {
        return '第二項頂點已不存在';
      }
    } else {
      return '第一項頂點已不存在';
    }
  }

	printGraph(){
  	console.log(this.adjacencyList)
  }
  
  //廣度優先
	bfs(start) {
      const queue = [start];
      const result = [];
      const visited = {};
      visited[start] = true;
      let currentVertex;
      while (queue.length) {
        currentVertex = queue.shift();
        result.push(currentVertex);
        this.adjacencyList[currentVertex].forEach(neighbor => {
          if (!visited[neighbor]) {
            visited[neighbor] = true;
            queue.push(neighbor);
          }
        });
      }
      return result;
  }
  
  //深度優先
  dfs(start) {
      const result = [];
      const stack = [start];
      const visited = {};
      visited[start] = true;
      let currentVertex;
      while (stack.length) {
        currentVertex = stack.pop();
        result.push(currentVertex);
        this.adjacencyList[currentVertex].forEach(neighbor => {
          if (!visited[neighbor]) {
            visited[neighbor] = true;
            stack.push(neighbor);
          }
        });
      }
      return result;
  }  

}

let graph = new Graph();

graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');

graph.addEdge('A', 'B');
graph.addEdge('A', 'D');
graph.addEdge('A', 'E');
graph.addEdge('B', 'C');
graph.addEdge('D', 'E');
graph.addEdge('E', 'F');
graph.addEdge('E', 'C');
graph.printGraph();
//{
//  A: ["B", "D", "E"],
//  B: ["A", "C"],
//  C: ["B", "E"],
//  D: ["A", "E"],
//  E: ["A", "D", "F", "C"],
//  F: ["E"]
//}

console.log(graph.bfs('A'))
//["A", "B", "D", "E", "C", "F"]
console.log(graph.dfs('A'))
//["A", "E", "C", "F", "D", "B"]
console.log(graph.dfs('B'))
//["B", "C", "E", "F", "D", "A"]
console.log(graph.dfs('C'))
//["C", "E", "F", "D", "A", "B"]
console.log(graph.dfs('D'))
//["D", "E", "C", "B", "F", "A"]
console.log(graph.dfs('E'))
//["E", "C", "B", "F", "D", "A"]
console.log(graph.dfs('F'))
//["F", "E", "C", "B", "D", "A"]

Python

#Graph
graph = {
    'A': ["B", "D", "E"],
    'B': ["A", "C"],
    'C': ["B", "E"],
    'D': ["A", "E"],
    'E': ["A", "D", "F", "C"],
    'F': ["E"]     
}
def bfs(graph,start):
    queue = []
    queue.append(start)
    result = []
    visited = set()
    visited.add(start)
    while(len(queue)>0):
        currentVertex = queue.pop(0)
        result.append(currentVertex)
        for neighbor in graph[currentVertex]:
            if neighbor not in visited:
                queue.append(neighbor)
                visited.add(neighbor)
    return result
def dfs(graph,start):
    stack = []
    result = []
    stack.append(start)
    visited = set()
    visited.add(start)
    while(len(stack)>0):
        currentVertex = stack.pop()
        result.append(currentVertex)
        for neighbor in graph[currentVertex]:
            if neighbor not in visited:
                stack.append(neighbor)
                visited.add(neighbor)
    return result


print(bfs(graph,'A'))
#['A', 'B', 'D', 'E', 'C', 'F']

print(dfs(graph,'A'))
#['A', 'E', 'C', 'F', 'D', 'B']