今天我們接續昨天的話題，繼續來聊聊AI領域裡面比較有趣的一些演算法。

螞蟻演算法 (Ant Colony Optimization, ACO）

如同我們昨天所聊到的，AI裡面有許多演算法都是模擬自然界的生物特性所發展出來的，螞蟻演算法顧名思義，就是模擬自然界裡螞蟻的習性所衍生出來的演算法。如果要講的比較精確一點的話，
螞蟻系統 (Ant System, AS)
是最早被提出來的模型，而螞蟻系統的理論也是現在其他螞蟻演算法的基礎。
而
螞蟻演算法 (Ant Colony Optimization, ACO）
則是目前應用較為廣泛的演算法。

那麼螞蟻演算法模擬的部份是什麼呢?
自然界中的螞蟻在外出找尋食物的時候，會在走過得路徑上留下一種叫做 費洛蒙(Pheromone) 的物質，而費洛蒙可以幫助後面的螞蟻來決定是否要依循著前面螞蟻留下的費洛蒙繼續前進。
想像一群螞蟻出門尋找食物的時候，先遣的螞蟻們是漫無目的且隨機的選擇移動的路徑並且沿路留下費落蒙，而後續出發的螞蟻遇到前蟻留下來的費落蒙時，會選擇：

1. 對哇造！ 螞蟻選擇跟著走，並且也留下自己的費洛蒙。
   這麼一來這條路徑的費洛蒙的濃度就會因此增加。
   

2. 螞蟻一定要靠自己！ 螞蟻選擇自己找尋沒有費洛蒙的路徑，並留下新的費洛蒙。
   如此一來原本有前蟻費洛蒙的路徑上，費洛蒙濃度將隨著時間而揮發減少。
   

而這些找尋食物的路徑上，越短的路徑能夠讓螞蟻越快的往返於巢穴與食物之間，因此這些較短(通常也意味著較好)的路徑上自然而然的會留下濃度越高的費洛蒙，並吸引更多的螞蟻照著這條路徑去搬運食物。

圖源: 動物星球頻道(台灣)
不懂梗的請參考這裡

因此這樣的特性，讓螞蟻演算法可以很好的運用在尋找問題最佳解的應用上，特別是在於尋找最短路徑上的一些問題。

爬山法 (Hill Climbing)

爬山法是一種區域性搜尋的演算法，他的優點是簡單快速且容易實作，然而缺點也很明顯，就是它很容易卡在相對高點的解而非全域的最佳解。

不太好理解的話沒有關係，我們來看下面的說明：
爬山法的概念為，
每次都以"當下的位子狀態"，並且去估算"所有鄰居的狀態"後，往最佳的方向移動。
例如今天我們有一個5乘5的區域，每一個區域裡為1~25的任一數字(不重複出現)，而每次移動的規則為附近九宮格的一格，目標是找到最大的數字。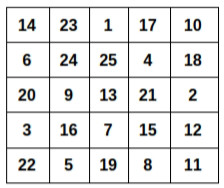

假設我們的初始位子從最右下方的 11開始，此時他的鄰居為九宮格內可以到達的數字，分別為12、15以及8，此時依照目標我們選擇最大的15來移動。
接下來我們的位子改成從15開始來做搜尋，在這個時候鄰居改成周圍九宮格裡的13、21、2、7、12、19、8以及11，那麼我們一樣依照目標選擇最大的21來移動成為新的起始點。
而接著我們從21做搜尋的時候，附近的鄰居為25、4、18、13、2、7、15以及12，到此我們選擇最大的25成為新的起點。
接著在25開始，我們可以看到周圍的鄰居已經沒有比自己還要大的數字了，則演算法結束，25為我們找到的解 (同時也是最佳解)。

爬山法雖然快又有效，但就如同前面所提到的缺點，爬山法很容易卡在相對高點的解而非全域的最佳解。.
上面舉的例子可以想像成是最佳情況，假設今天我們選的起點為左中下的3，那麼在經過第一次搜尋並且移動後，就會來到相對於附近已經是最佳解的22並停止搜尋，也就是只有找到相對於自己鄰居中最佳的解而非整個25宮格裡面的全域的最佳解 25。
甚至更慘一點的情況，我們從正下方的19開始當作起點，此時由於已經在相對高點了，因此搜尋結束並且回報19為最佳解。

我們從這張圖來看的話：

圖源

如果想要找到全域最佳解 (Global maximum)，那麼你起始搜尋的位置必須得在最高點位左方shoulder到右邊最低點位之間才有機會，否則的話根據爬山法的機制，只要移動到任何一個平坦處 (如圖右邊的flat local maximum)或是相對高點 (如圖中間的Local maximum)，則結束搜尋並且只能得到局部最佳解。

當然後續也有許多對於爬山法所作的改良，例如：
在爬山的過程中加入一些隨機性、改變爬山搜尋時的策略、更多元化且多次的重新設定起始點來做搜尋等等，這些細節在這邊我們就不多談了。

不小心又打了三千五百多個字...
我們明天繼續 (或是停刊放棄)