BFS是簡寫，全名是Breadth-First Search(廣度優先搜尋演算法)
BFS跟DFS一樣，也是搜尋的演算法，一樣是很常見哦！
DFS是以深度為優先，每一條路都會搜尋到盡頭，BFS的做法不一樣是以廣度優先，會把旁邊的都搜尋完再擴散出去。

來看一下圖: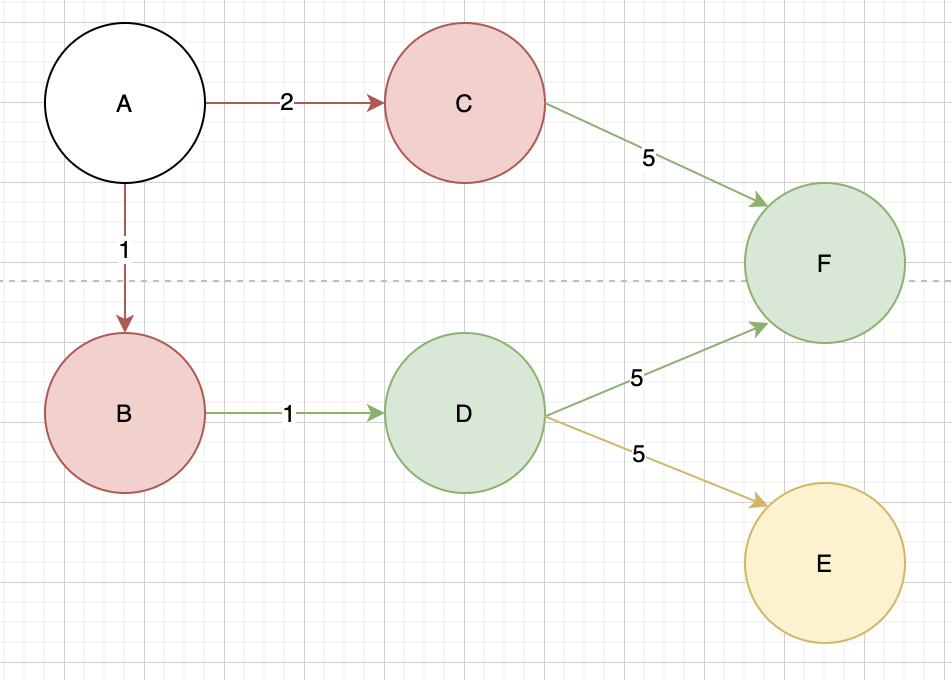

一樣是從A作為起點，先把旁邊的都走完，再往外去找。
A先找到B、C(紅)，走完了再往外找，B下一個是D(綠)，C下一個是F(綠)，最後D再走到E(黃)

我們需要來一個Queue，來記錄接下來要走的頂點，把每一個要走的頂點放到Queue裡面，再用一個index去控制順序。
ex:
我先從A點開始走

queue: [A]
index: 0

A會先遇到B、C，再沒有邊了，就把index++

queue: [A,B,C]
index: 1

再從頂點B的邊去搜尋，找到D，最後一樣把index++

queue: [A,B,C,D]
index: 2

再重複這個過程，把每一個頂點的邊走完就可以了～

程式:

func (g *Graph) BFS(target *Vertex) {
	visted := g.getVistedVertex() // 用來記錄走過的頂點
	visted[target] = true
	queue := []*Vertex{
		target,
	}

	index := 0
	for index < len(queue) {
		for _, edge := range g.adjList[queue[index]] {
			if !visted[edge.Vertex] {
				fmt.Printf("vist: %v \n", edge.Vertex.Name)
				queue = append(queue, edge.Vertex)
				visted[edge.Vertex] = true
			}
		}

		index++
	}
}

func main() {
	a := &Vertex{
		Name: "A",
	}
	b := &Vertex{
		Name: "B",
	}
	c := &Vertex{
		Name: "C",
	}
	d := &Vertex{
		Name: "D",
	}
	e := &Vertex{
		Name: "E",
	}
	f := &Vertex{
		Name: "F",
	}

	g := newGraph()
	g.AddVertex(a)
	g.AddVertex(b)
	g.AddVertex(c)
	g.AddVertex(d)
	g.AddVertex(e)
	g.AddVertex(f)

	// A的邊
	g.AddEage(a, b, 1)
	g.AddEage(a, c, 2)
	// B的邊
	g.AddEage(b, d, 1)
	// C的邊
	g.AddEage(c, f, 5)
	// D的邊
	g.AddEage(d, e, 5)
	g.AddEage(d, f, 6)

	g.BFS(a)
}

output:

vist: B 
vist: C 
vist: D 
vist: F 
vist: E

一般情境來說用BFS跟DFS都可以解決問題
BFS比DFS要用更多的記憶體，因為多一個Queue去記頂點，如果要省記憶體可以用DFS
如果是要找目標附近的東西，用BFS會比較適合～

明天來講最短路徑～