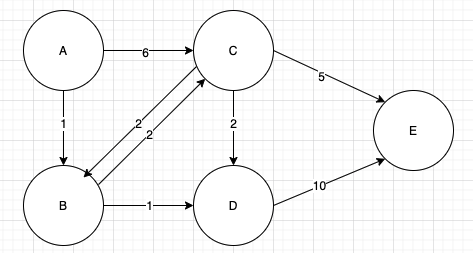
如果我們想知道A點到E點之間的最短路徑,我們要怎麼做?
在邊值不是負的情況下,都可以使用Dijkstra算法,像兩點之間的距離不存在負值,就很適合用Dijkstra,如果有負值的圖,需要用Bellman-Ford的算法。
Dijkstra算法是BFS的延伸,搜尋方式一樣是以廣度優先。
現在來大概說明一下算法的流程~
我們需要先定義一個map來記各點的最短距離
type ShortestPath struct {
Distance int
PreVertex *Vertex
}
map[*Vertex]*ShortestPath
從A點出發,先到B點,記錄到B的最短距離為1。A再去C點,到C最短距離為6。
現在map的記錄為:
B: {Distance:1, PreVertex:A}
C: {Distance:6, PreVertex:A}
A已經走完了,現在換B、C往外搜尋
B到C的距離為2,A到B的距離+2=3,目前map裡面C的最短路離為6,3<6,更新C最短距離為3
B到D距離1,A到B的距離+1=2,更新D最短距離為2
C到E,距離為3+5=8,更新E最短距離
C到B,距離為6+2=8,大於原本的1,不更新
map:
B: {Distance:1, PreVertex:A}
C: {Distance:3, PreVertex:B}
D: {Distance:2, PreVertex:B}
E: {Distance:8, PreVertex:C}
重複這個過程,把全部的點跟邊都走完,就可以得知從A出發全部點的最短距離~
如果我們要知道整個路徑的走法,就從PreVertex回溯就可以了
ex. E->C->B->A
程序:
type ShortestPath struct {
Distance int
PreVertex *Vertex
}
func (g *Graph) Dijkstra(target *Vertex) map[*Vertex]*ShortestPath {
path := map[*Vertex]*ShortestPath{}
visted := g.getVistedVertex() // 用來記錄走過的頂點
visted[target] = true
queue := []*Vertex{
target,
}
// 初始化距離
for v := range visted {
path[v] = &ShortestPath{
Distance: 0,
}
}
index := 0
for index < len(queue) {
for _, edge := range g.adjList[queue[index]] {
if !visted[edge.Vertex] {
queue = append(queue, edge.Vertex)
visted[edge.Vertex] = true
}
// 目前vertex的最短距離 + edge的距離
totalDistance := path[queue[index]].Distance + edge.Distance
// 第一次到這個點 or 距離比較近 就去更新最短路徑
if path[edge.Vertex].Distance == 0 || path[edge.Vertex].Distance > totalDistance {
path[edge.Vertex] = &ShortestPath{
Distance: totalDistance,
PreVertex: queue[index],
}
}
}
index++
}
return path
}
// 顯示出整個路徑
func (g *Graph) ShowShortestPath(start *Vertex, end *Vertex) {
allPath := g.Dijkstra(start)
vertexPath := []*Vertex{}
path := allPath[end]
distance := path.Distance
for path.PreVertex != nil {
vertexPath = append(vertexPath, path.PreVertex)
path = allPath[path.PreVertex]
}
str := ""
for i := len(vertexPath) - 1; i >= 0; i-- {
str += vertexPath[i].Name + "->"
}
str += end.Name
fmt.Printf("distance: %v, path: %v \n", distance, str)
}
func main() {
a := &Vertex{
Name: "A",
}
b := &Vertex{
Name: "B",
}
c := &Vertex{
Name: "C",
}
d := &Vertex{
Name: "D",
}
e := &Vertex{
Name: "E",
}
g := newGraph()
g.AddVertex(a)
g.AddVertex(b)
g.AddVertex(c)
g.AddVertex(d)
g.AddVertex(e)
// A的邊
g.AddEage(a, b, 1)
g.AddEage(a, c, 6)
// B的邊
g.AddEage(b, c, 2)
g.AddEage(b, d, 1)
// C的邊
g.AddEage(c, b, 2)
g.AddEage(c, d, 2)
g.AddEage(c, e, 5)
// D的邊
g.AddEage(d, e, 10)
g.ShowShortestPath(a, e)
}
output:
distance: 8, path: A->B->C->E
明天來解leetcode~
