Q1. Floyd-Warshall 是什麼

一種利用 Dynamic Programming ，求 Graph 中兩點之間最短路徑的演算法。

考慮 A, B 兩點之間的最短路徑，若有經過 k 點，則：

A, B 兩點之間的最短路徑 = A, k 兩點之間的最短路徑 + k, B 兩點之間的最短路徑

我們可以將含有 n 個節點的最短路徑問題分解成 n 個「是否經過第 k 點」的問題。

以下圖為例，計算 節點 0 與 節點 3 之間的最短路徑長。由於 節點 0 和 節點 3 作為起點與終點，必然會在路徑中被經過，因此我們將「路徑只經過 節點 0 和 節點 3 」作為初始狀態，再陸續考慮最短路徑是否會經過其他節點。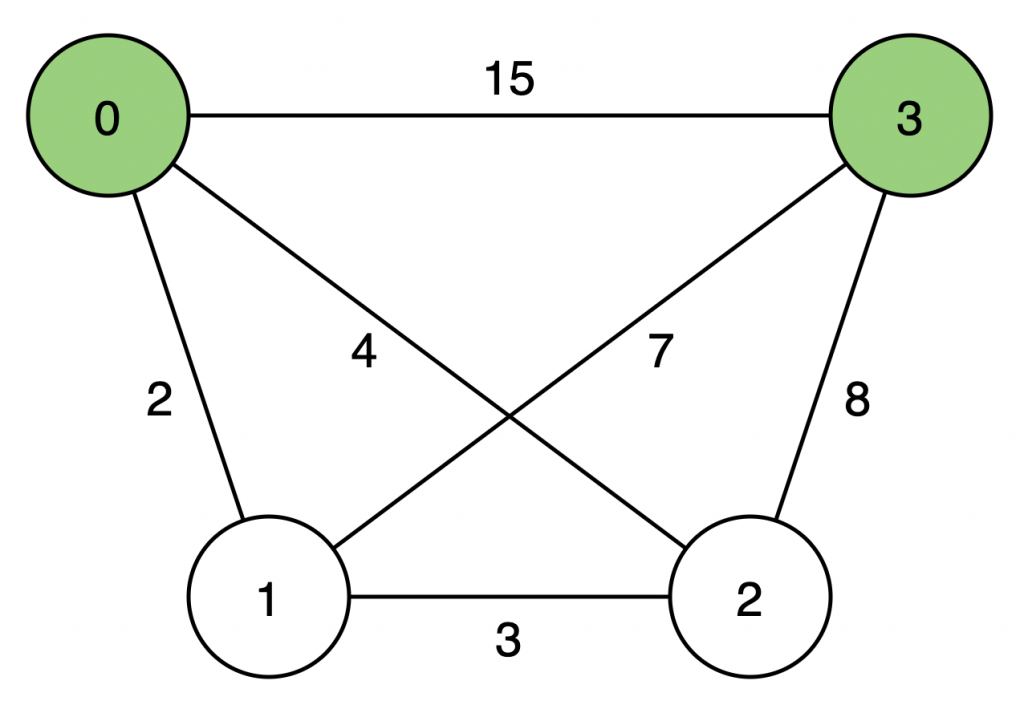

1. 初始狀態，最短路徑長為 15：
   

2. 考慮 節點 1 是否為中繼站之一：

   • 如果是，則路徑長應為 節點 0 到節點 1 的最短路徑長 + 節點 1 到 節點 3 的最短路徑長
   • 如果否，則路徑長應不受節點 1 影響，而是原先尚未考慮節點 1 時的路徑長。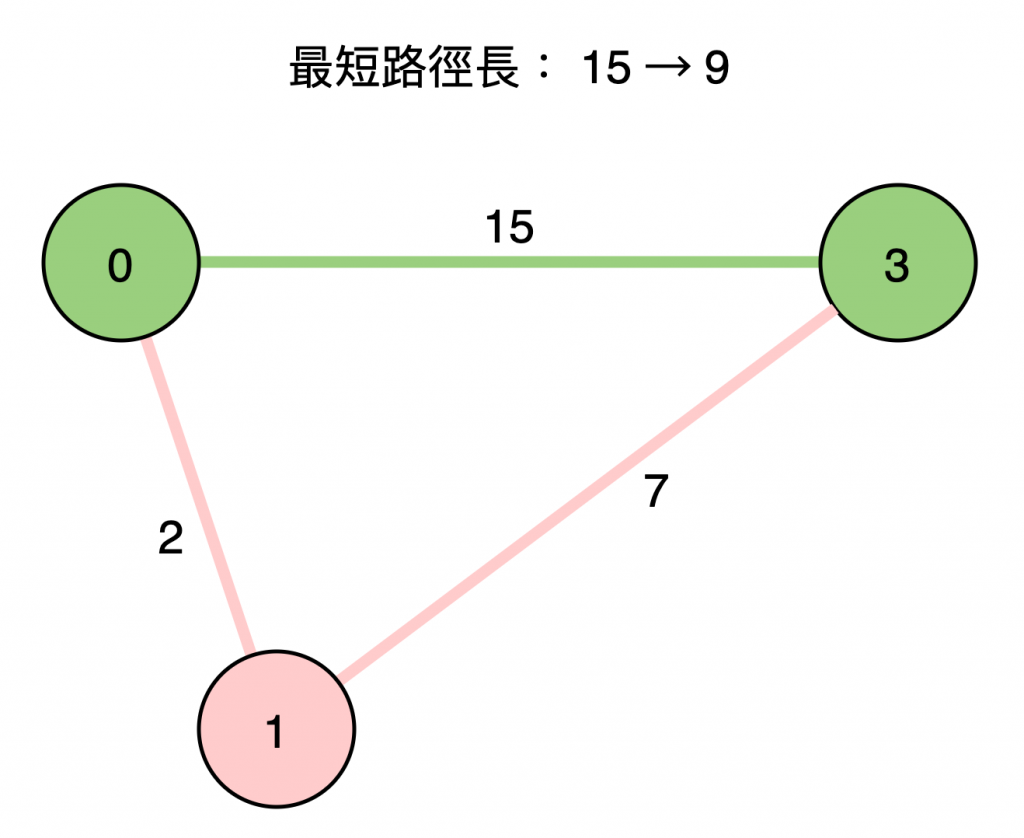

• 在此例中，經過 k 可以得到較短的路徑長 9
  

3. 繼續考慮下一個節點，直到所有節點都計算過：
   以此例而言，若經過 節點 2 ，其路徑長為 12，沒有比原先的路徑長短，因此最終得到答案為 9 。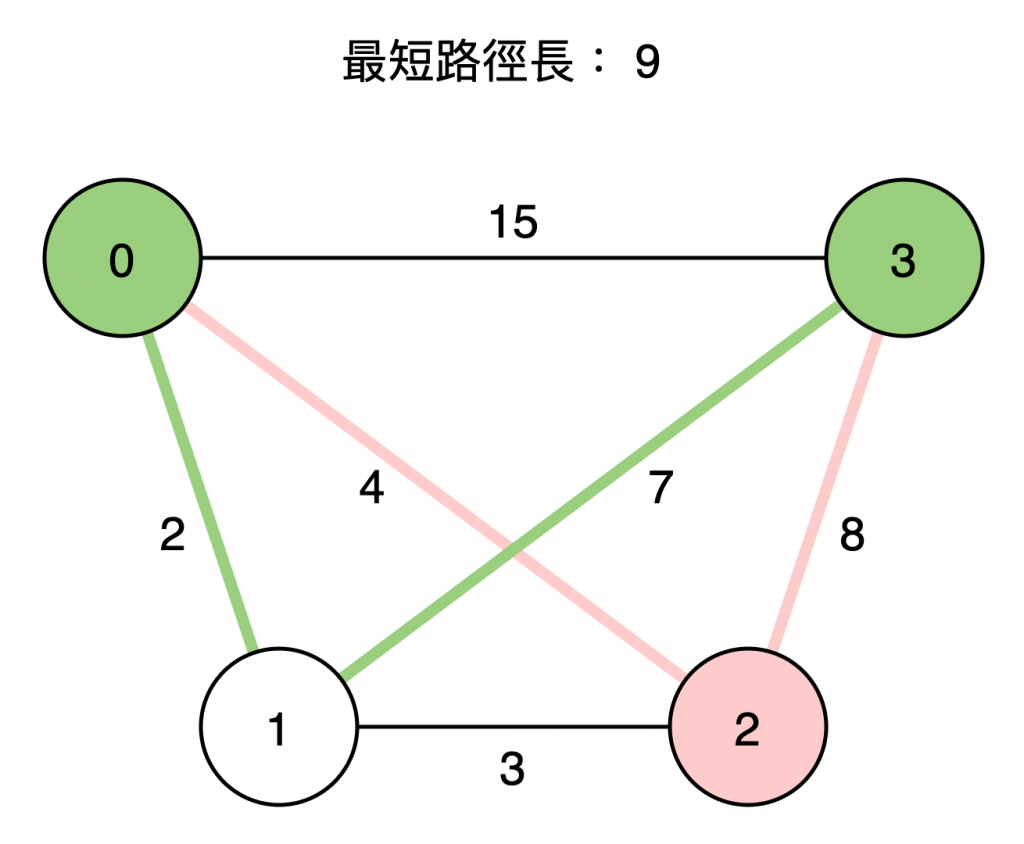
   

• 從上述例子中，可以歸納出下列關係：

• 假設已經考慮了 k - 1 個節點，現在要考慮第 k 個節點是否為最短路徑中的中繼站，會有兩種可能的最短路徑：

  • 最短路徑有經過 k 點：其路徑長為 A, k 兩點之間的最短路徑長 + k, B 兩點之間的最短路徑長
  • 最短路徑沒有經過 k 點：則表示最短路徑沒有經過 k 點，因此最短路徑與未考慮 k 點時相同。

• 在兩種可能路徑中，較短者方為真正的最短路徑。

• 綜上所述，可列出以下遞迴關係式：

考慮 k 個中繼節點時， AB 之間的最短路徑長 = min(
	Ak 兩點之間的最短路徑長 + kB 兩點之間的最短路徑長,
	考慮 k - 1 個中繼節點時， AB 之間的最短路徑長
)

# 令 d(A, B, k) 表示 「考慮 k 個中繼節點時， AB 之間的最短路徑長」
=> d(A, B, k) = min( 
                    d(A, k, k - 1) + d(k, B, k - 1),
                    d(A, B, k - 1)
                    )

• 可以發現，當我們在計算 AB 之間的最短路徑 時，會需要考慮 Ak 兩點之間的最短路徑長 和 kB 兩點之間的最短路徑長，縱然在上述例子中可以很容易的算出來，但回顧遞迴關係式，其中的 d(A, k, k - 1) + d(k, B, k - 1) 要每次都計算的話，不僅不好實作，也耗費效能，因此此時正是使用 Dynamic Programming 的時機 (DP：將已經計算好的結果記錄下來，下一次使用就可以拿)。

• Floyd-Warshall 的實作邏輯

1. 先計算每個點直達另一個點的成本/權重/距離。 (若無法直達，則以無限大代表)
2. 總共有 0~N 個點，我們依序計算 min(原本的成本, 經過第k個點的成本)

• 以下圖為例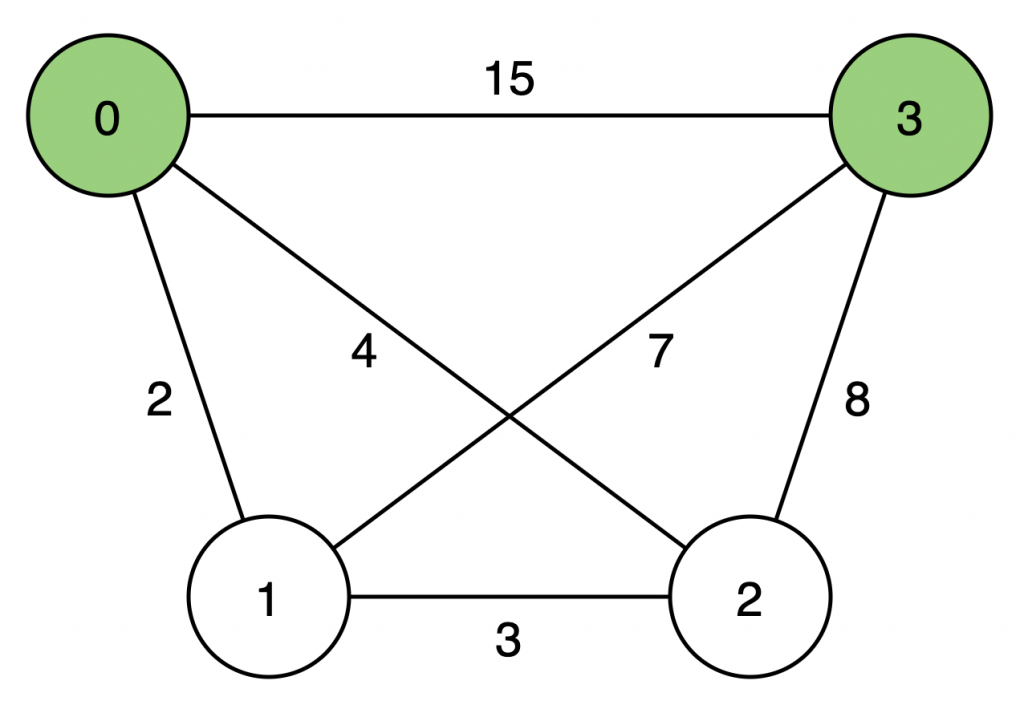
  

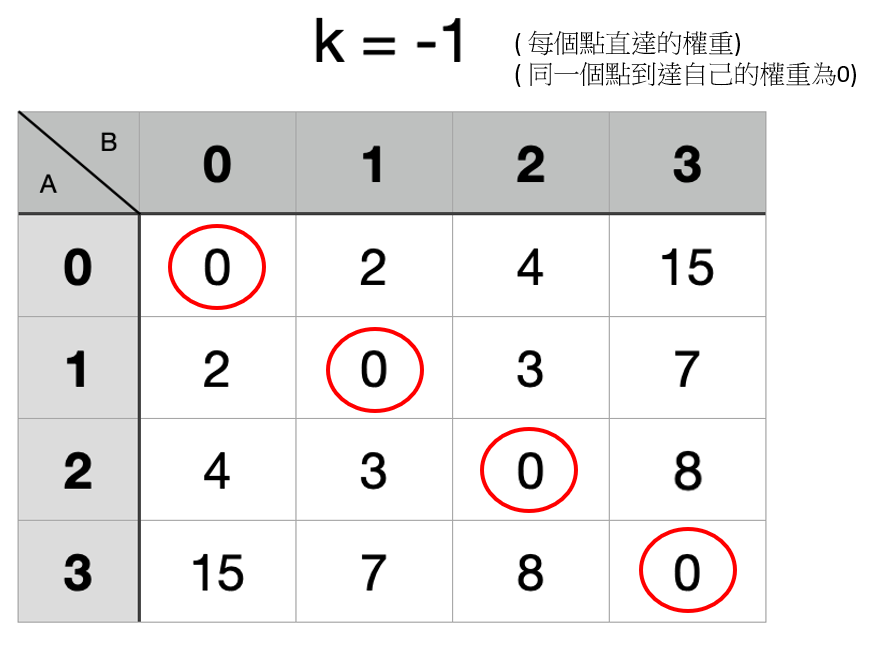
  • 我們先計算每個點直達其他點的成本
    

• 接著我們依序計算計算經過 第0點的成本、第1點的成本...第3點的成本

  • 首先是經過第 0 點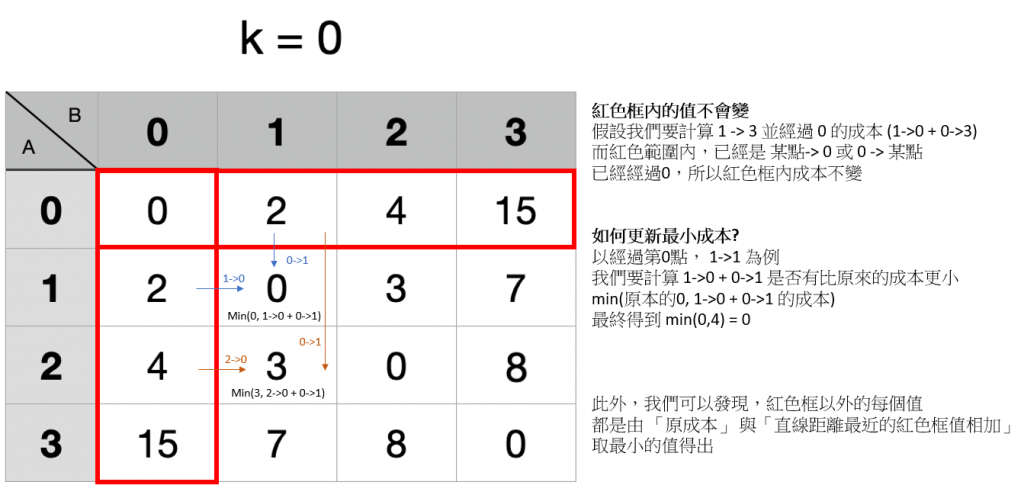
    

  • 接著是經過第 1 點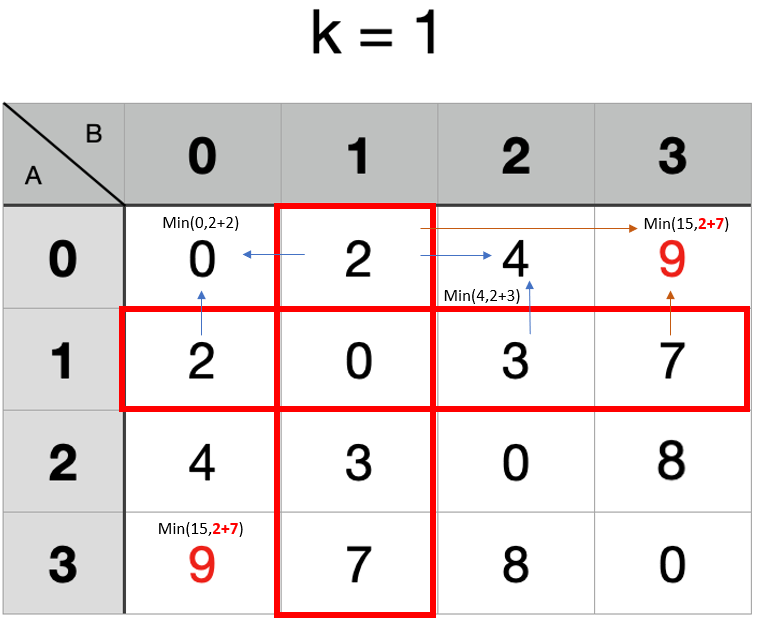
    

  • 接著是經過第2點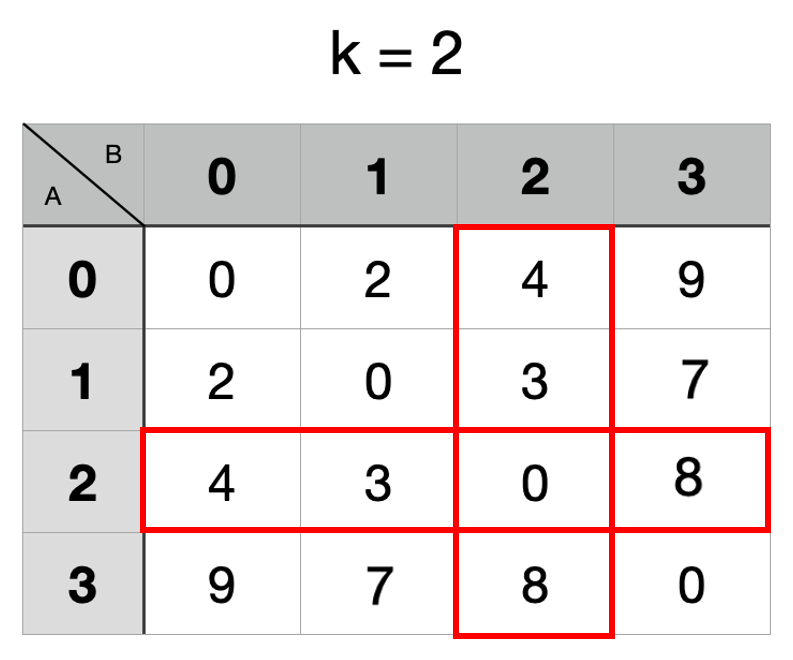
    

  • 最後是經過第3點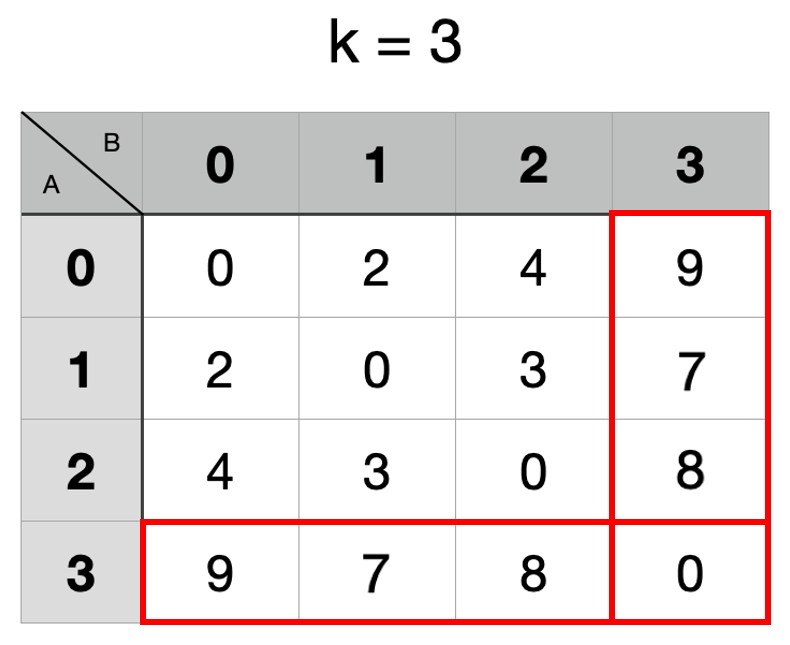
    

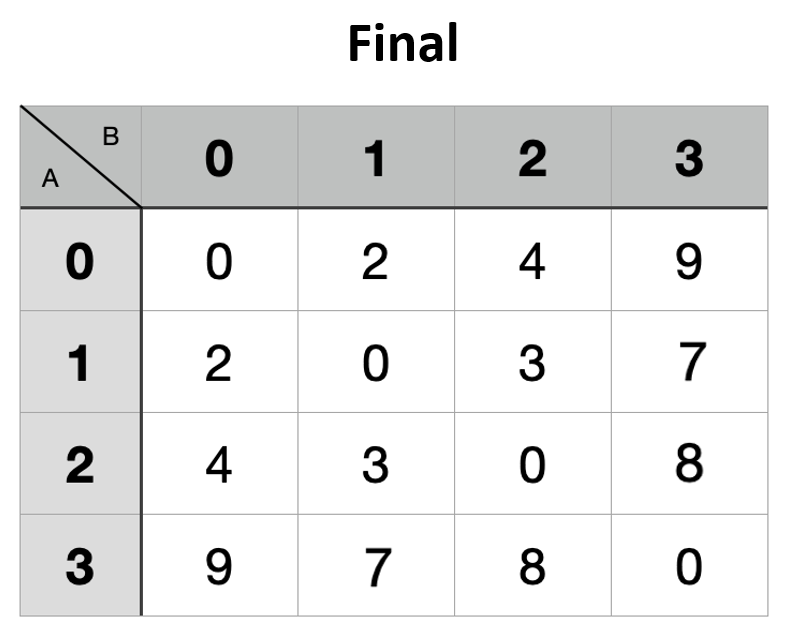
• 計算完，這個表格就會是某個點抵達另外一個點最短距離，回到題目，我們要求 0→3 最短距離，可以從表格中得知最短距離為 9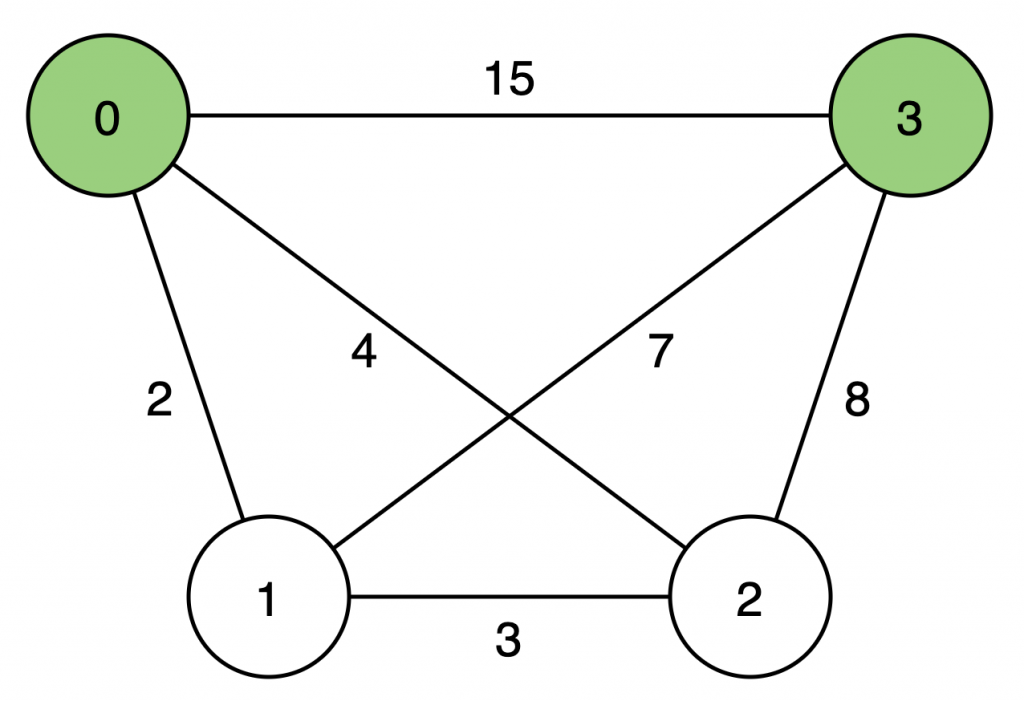
  
  

• 在以下情況不適合使用 Floyd-Warshall 計算最短路徑

  • 當繞一個 cycle 後為負，也就是負週期的情況 (可能導致負無窮大)
  • 節點數量過多 (導致時間複雜度過高)

Q2. 學會 Floyd-Warshall 概念可以做什麼 ?

• 求 Graph 中兩點之間的最短路徑 (在無負週期情況下)

Lab. 明天要解的題目：1334. Find the City With the Smallest Number of Neighbors at a Threshold Distance

• 題目連結：https://leetcode.com/problems/find-the-city-with-the-smallest-number-of-neighbors-at-a-threshold-distance/

• 題目敘述

  • 有 n 個城市，編號從 0 ~ n-1，題目會給一些邊，從 i 點到 j 點的權重
  • distanceThreshold 類似遊戲中的精力值，最多只能走 distanceThreshold 的路
  • 題目要找出一個城市，它到達其他城市數目最少
    • 若有多個到達數量一樣少的城市，則回傳編號最大的

  

• 測資的 Input/Output

  • 有 n 個城市
  • edges 為城市到城市間的路徑權重
  • distanceThreshold 類似精力值，你走的路徑權重和不得大於 distanceThreshold
  • 回傳能夠抵達最少數量的城市，若有多個這樣的情況，則回傳編號最大的城市
    • 以範例1為例，city 0 與 city 3 都只能抵達兩個城市，則回傳編號較大的 city 3
      

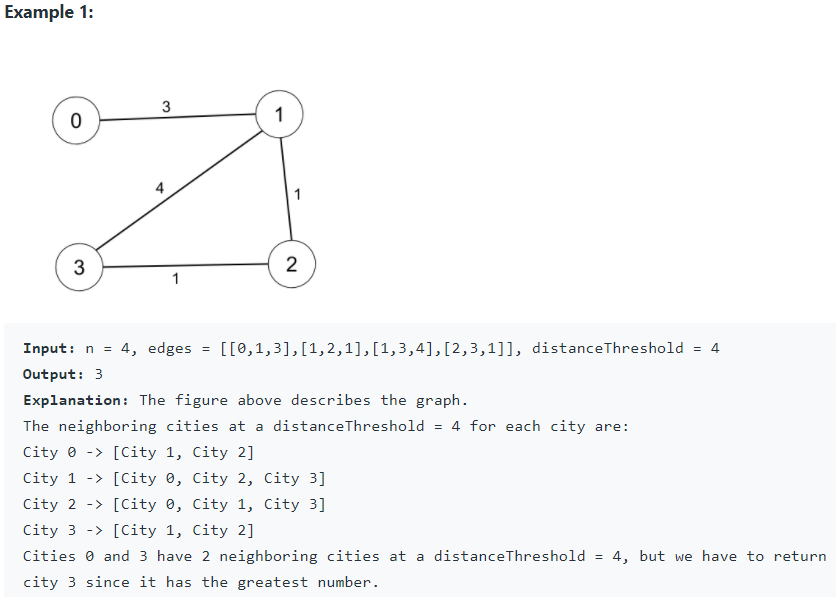
• 題目的條件

  • 城市為 2~100 個
  • 路徑為 1~ n*(n-1) 條
  • edges 固定為三個一組 [從i點,到j點,的權重]
  • 城市每一點編號為 0 ~ n-1
  • 權重與 distanceThreshold 介於 1~10000 (皆為正數，無負週期)