• 先簡單回顧一下，今天預計分析的題目：

• 題目連結：https://leetcode.com/problems/path-with-maximum-probability/

• 題目敘述

  • 題目給 n 個節點，並且 edges 會儲存從 a 點到 b 點的邊(無向圖)，succProb 儲存 a 點到 b 點的「成功概率」
  • 計算從 start 點到 end 點的最大成功機率，若無法抵達，則回傳0
    

• 測資的 Input/Output

  • 如範例1，第0點抵達第2點有兩種走法： 0→1→2 與 0→2
  • 需要回傳 start → end 點最高成功機率： max(0→1→2 ,0→2) = max(0.5*0.5,0.2) = 0.25
    
    

程式邏輯

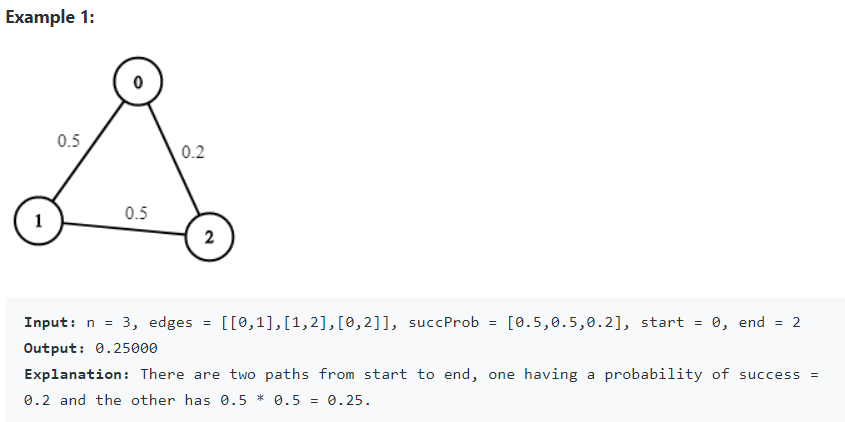
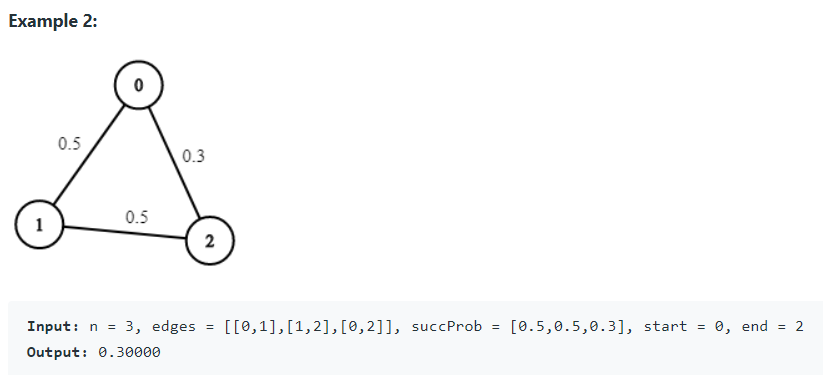
• 由於 n 可能到 10000，用二維陣列儲存 edge 的話，效能不佳。因此此處使用 list 的方式紀錄每一點存在的邊。

  mapping = [[] for _ in range(n)]
  for i in range(len(edges)):
      (a, b), prob = edges[i], succProb[i]
      mapping[a].append((b, prob))
      mapping[b].append((a, prob))
  

• 雖然是求最大機率，但由於機率相乘只會越來越小 （因為機率 ≤ 1），正好可以使用 dijkstra 來解此問題。

  • dijkstra 找尋最短路徑的條件是不能有負權重，也就是每走過一個節點，必然會 新的路徑長 ≥ 原始路徑長 。
  • 若是將機率乘以負號，大小反轉，正好就變成求最小機率，並且每走過一個節點， 新的權重≥ 原始權重。

• 使用 dijkstra 演算法，我們需要開一個一維陣列儲存最大機率（最短路徑）。

  maxProb = [0] * n
  maxProb[start] = 1
  

  • 起點走到自己的機率是 100% ，因而設為 1 。
  • 換個方式解讀就是自己走到自己，路徑長仍然不變 1 x 1 = 1 。

• 依據 Dijkstra，每一輪要找出機率最大者進行走訪（路徑長最小者），然而如果每一輪都要掃描一次找出最大值，會嚴重影響效能，導致 TLE，此處我們使用 priority queue 來實作。

  • 開一個 queue，放入起點及其機率。由於 Python 的 Priority queue 預設是由小到大，為了能取到最大機率，這邊將權重放入前後都要乘以負號，反轉大小。

  pq = [(-1, start)]
  

  • 用迴圈每次取最大機率者

  while pq:
  curProb, cur = heapq.heappop(pq)
  curProb = -curProb
  

  • 若當前取到的節點為欲計算的終點，則我們已然找到其最大機率，後面就不需要再做下去了。

  if cur == end: break
  

• 若還沒走到終點，則以現在的節點出發，若能走出更大的機率，就將該節點與機率放入 queue 中。

  for i, prob in mapping[cur]:
      newProb = curProb * prob
      if newProb > maxProb[i]:
          maxProb[i] = newProb
          heapq.heappush(pq, (-newProb, i)) 
  

  • 由於 priority queue 會幫助我們先取到最大機率者，所以即便以前對同個節點放入過較小的機率也無妨，會被自動丟到後面去。

• 最後，回傳走到終點最大機率

  return maxProb[end]
  

• 完整程式碼如下：

class Solution:
    def maxProbability(self, n: int, edges: List[List[int]], succProb: List[float], start: int, end: int) -> float:
        mapping = [[] for _ in range(n)]
        for i in range(len(edges)):
            (a, b), prob = edges[i], succProb[i]
            mapping[a].append((b, prob))
            mapping[b].append((a, prob))

        maxProb = [0] * n
        maxProb[start] = 1
        
        pq = [(-1, start)]
        while pq:
            curProb, cur = heapq.heappop(pq)
            curProb = -curProb
            
            if cur == end: break
            for i, prob in mapping[cur]:
                newProb = curProb * prob
                if newProb > maxProb[i]:
                    maxProb[i] = newProb
                    heapq.heappush(pq, (-newProb, i))        
        return maxProb[end]

heapq 參考資料：https://docs.python.org/zh-tw/3/library/heapq.html