Q1. Dijkstra 是什麼?

• 一種利用 Dynamic Programming ，與 Floyd-Warshall 一樣，是求 Graph 中兩點之間最短路徑的演算法。
• Floyd-Warshall 是計算「每一個點」到其他點的最短路徑
• Dijkstra 是計算「某一個點」到其他點的最短距離

條件限制：

Dijkstra 適用的 graph 中，不可以有負權重的邊。

流程：

1. 選擇一個起點，以下圖為例，我們假設起點為第 0 點

2. 將起點「直接相鄰」的節點權重視為最短路徑長，其他結點的路徑長則視為無限大。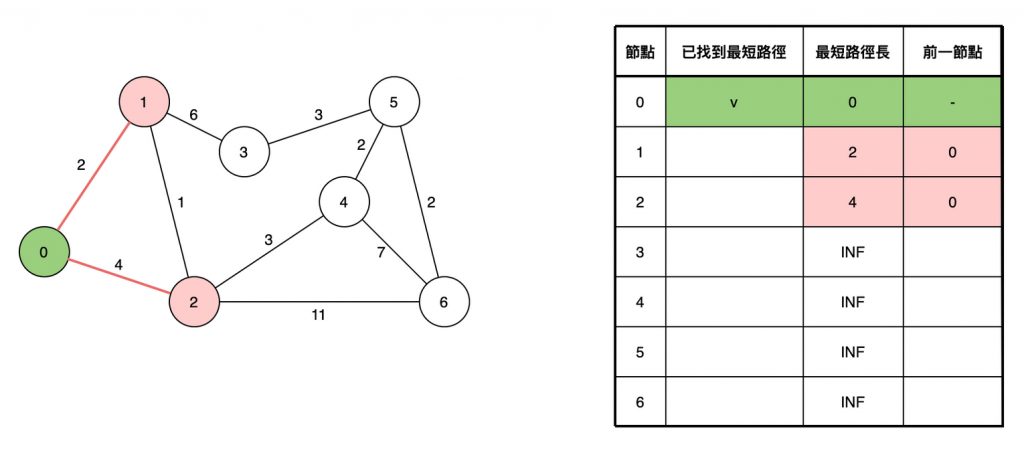
   

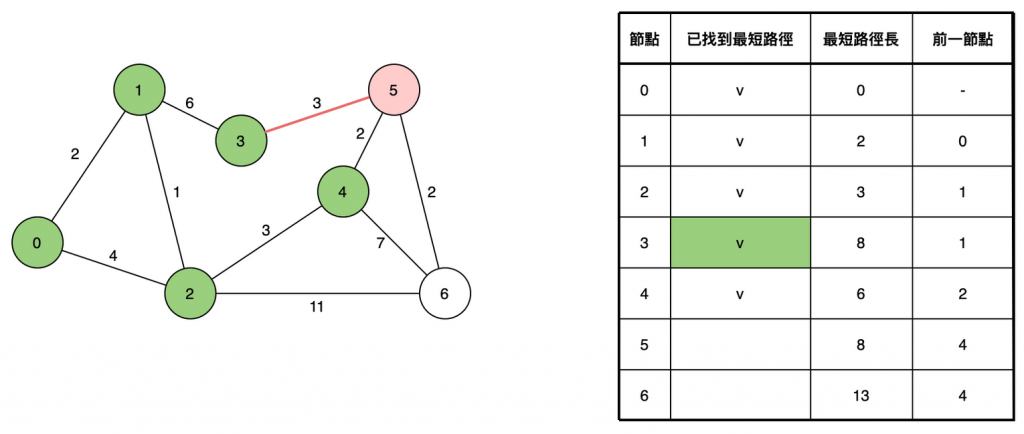
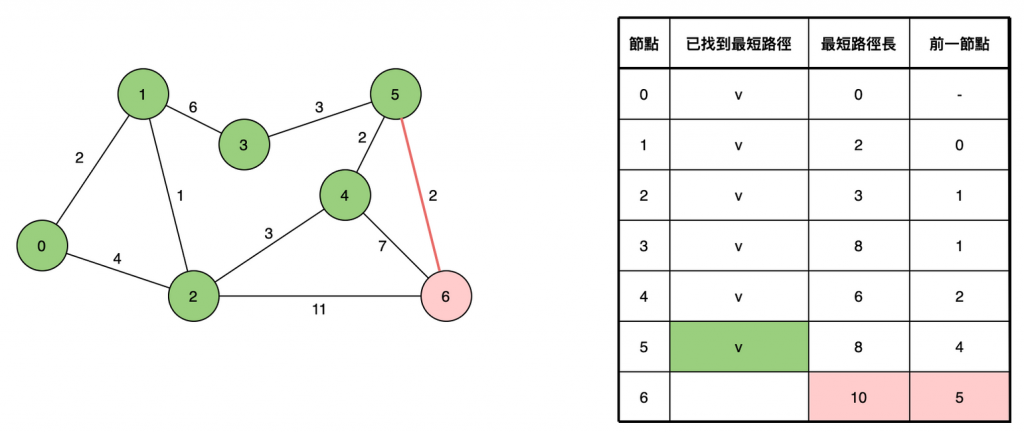
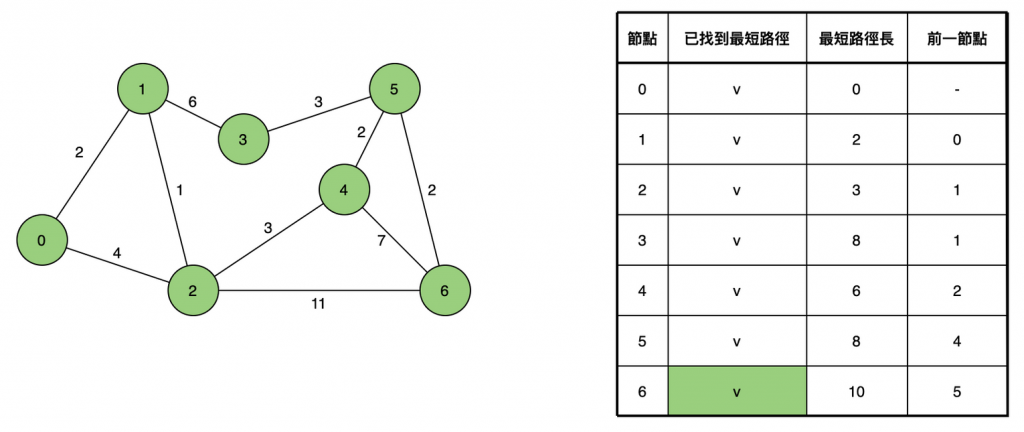
3. 選取距離最近的節點，如 0→1 與 0→2 兩條路徑，選擇第1點目前路徑較短的開始看，由於不可能有其他路徑比當前的更短了（因為圖中無負權重，要從其他節點過來一定會更遠），我們可以確定此距離就是真正的最短距離。

4. 從當前選取的節點(第1點)出發前往其他節點(相鄰的點有2與3)，如果能比已知的路徑長更短(0→2原本紀錄為4，0→1→2=3，選最短路徑的3)，就更新已知的路徑長；如果需要知道最短路徑的確切節點，可以在更新時一併紀錄前一節點。

5. 反覆 3 ~ 5 ，直到所有節點都找到最短路徑。
   

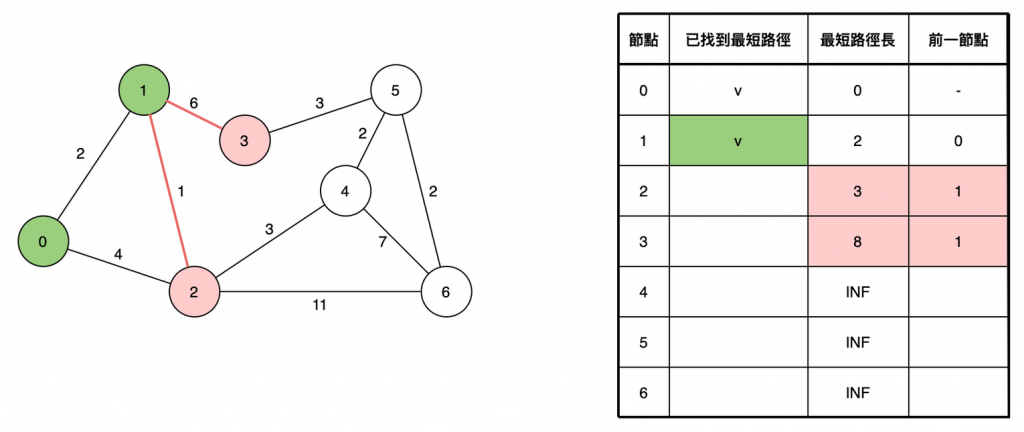
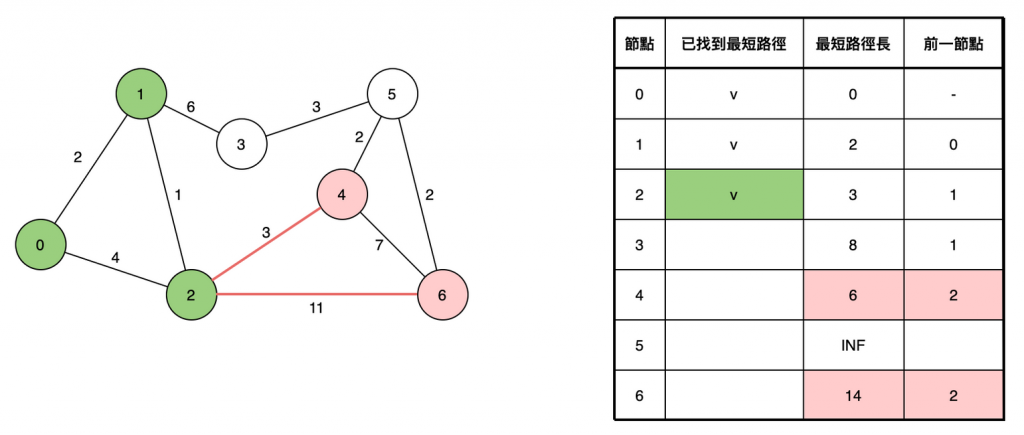
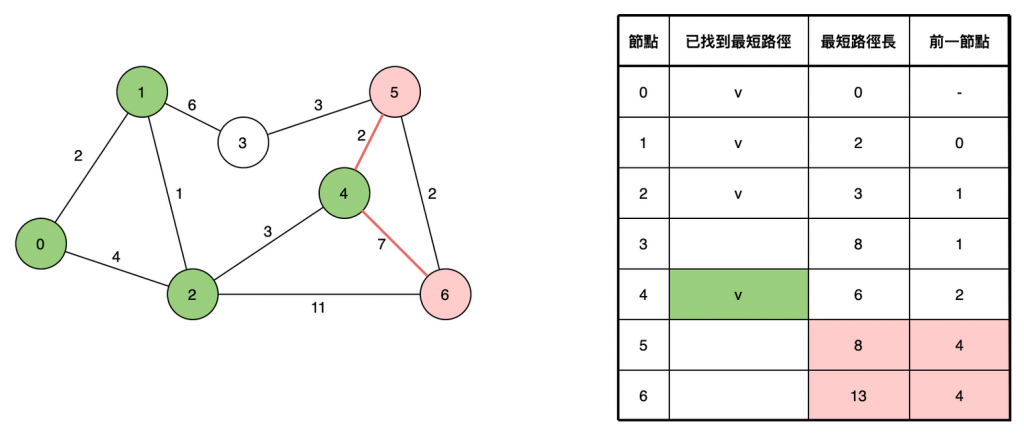
參考資料：https://ithelp.ithome.com.tw/articles/10209593

參考資料：https://ithelp.ithome.com.tw/articles/10238059

Q2. 學會 Dijkstra 概念可以做什麼 ?

可以求 Graph 中兩點之間的最短路徑。

Lab. 明天要解的題目：1514. Path with Maximum Probability

• 題目連結：https://leetcode.com/problems/path-with-maximum-probability/

• 題目敘述

  • 題目給 n 個節點，並且 edges 會儲存從 a 點到 b 點的邊(無向圖)，succProb 儲存 a 點到 b 點的「成功概率」
  • 計算從 start 點到 end 點的最大成功機率，若無法抵達，則回傳0
    

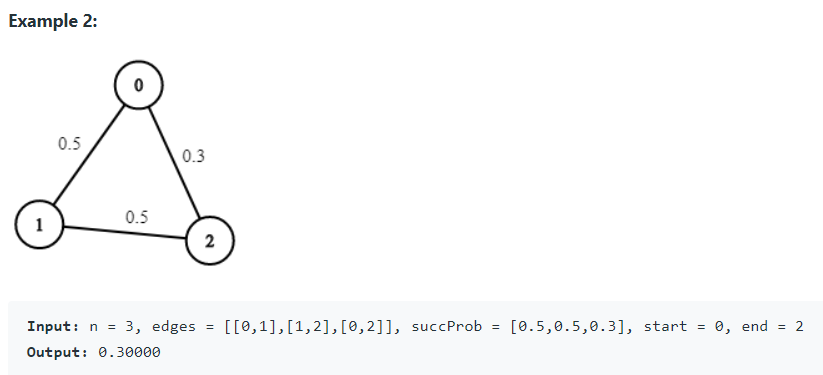
• 測資的 Input/Output

  • 如範例1，第0點抵達第2點有兩種走法： 0→1→2 與 0→2
  • 需要回傳 start → end 點最高成功機率： max(0→1→2 ,0→2) = max(0.5*0.5,0.2) = 0.25
    
    

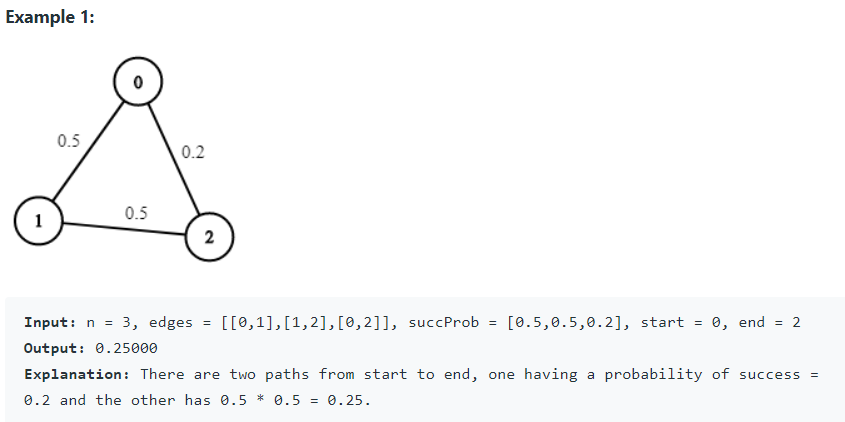
• 題目的條件

  • 會有 2~10000 個點
  • start 與 end 介於 0~10000 間
  • start 與 end 不會是同一個點
  • edges 中的點，會是介於 0~10000間
  • edges 所記錄的 a 點到 b 點不會是同一個點
  • 「edges 紀錄的邊長」會與 「succProb 的成功機率」數量相同，並介於 0~20000 間
  • succProb 成功機率介於 0~1 之間
  • 兩個點之間，最多只有一條邊