Colab連結

今天大家介紹 Gradient Exploding （梯度爆炸） 與 Gradient Vanishing (梯度消失)，並會簡單做個實驗觸發這兩者情況，實驗之前，簡單講解一下這兩者的區別。

梯度爆炸：

梯度(gradient) 是將真實值與預測值經過 loss 運算後，對其偏微分得到的量，這個量乘上學習率後即是權重的主要更新量，因此若梯度數值很大時，模型權重的變化量也會很大，如果今天梯度很大，權重就有可能從原本小數（如0.12），一更新變成102，又再一次更新變大成120000，直到變成無限大 inf，這也是我們所說的看到模型訓練到一半，loss 直接變 nan 給你看。

梯度消失：

另一個和梯度爆炸相反的立字就是梯度消失，也就是梯度的值非常小，小到權重幾乎不怎麼更新，像是 sigmoid 函數的微分最大僅有0.25，一但今天模型層數多時，梯度乘上多次的0.25有可能會變得非常的小，這時模型就幾乎不會更新了。

而導致梯度爆炸或消失的原因很多種，像是學習率設定不當、錯誤的模型權重初始化或模型結構設計有問題等都有可能會發生，要 debug 這個問題我建議先訓練少數的 epoch，觀察初始 loss 值是否過大過小或直接印出 layer 的權重值來觀察。

class PrintWeightsCallback(tf.keras.callbacks.Callback):
  def on_epoch_begin(self, epoch, logs=None):
    l1_w = self.model.layers[1].weights[0].numpy()[:6,0]
    print(f'layer1: {l1_w}')

如上所述，為了得知模型權重的狀況，我寫了一個 callback，每個 epoch 結束時，我就印出權重值。

而本次實驗為了能夠更快跑出爆炸/消失等問題，我決定手動調整資料集，目的是想要訓練一個模型當我今天 input 為 n 時，output 也剛好是 n 的回歸模型，loss採用 mean_squared_error。

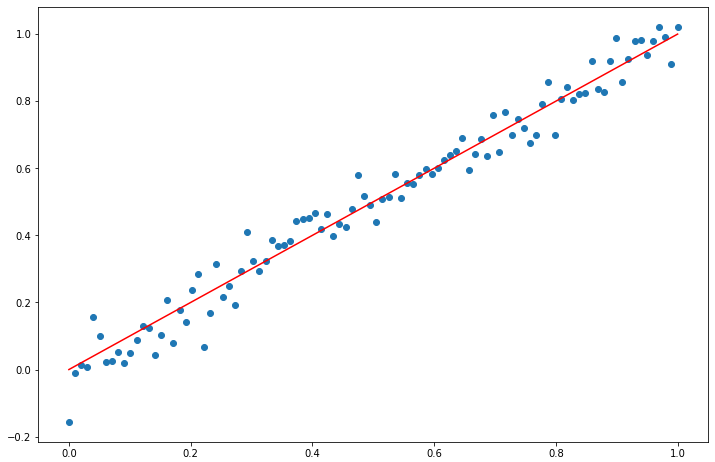
實驗一：資料集是100個從0到1的小數

x = np.linspace(0,1,100, dtype=np.float32)  # 介於[0,+1]之間的樣本
noise = np.random.normal(0, 0.05, x.shape).astype(np.float32)  # noise取樣本區間的5%, (1-0)*0.05=0.05
y = x
z = x + noise 

fig = plt.figure(figsize=(12,8))
plt.scatter(x,z)
plt.plot(x,y,color='red') 
plt.show()

train_data = tf.data.Dataset.from_tensor_slices((z,y))

ds_train = train_data.cache()
ds_train = ds_train.shuffle(SHUFFLE_SIZE)
ds_train = ds_train.batch(BATCH_SIZE)
ds_train = ds_train.prefetch(tf.data.experimental.AUTOTUNE)

model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, input_shape=(1,))) 
model.add(tf.keras.layers.Dense(1))
model.compile(loss=tf.keras.losses.mean_squared_error, 
              optimizer=tf.keras.optimizers.SGD(learning_rate=0.1))

history = model.fit(
    ds_train,
    epochs=EPOCHS,
    verbose=True,
    callbacks=[PrintWeightsCallback()])

產出:

Epoch 1/20
layer1: [ 0.07604259  0.27522993 -0.10235941  0.08207107 -0.04505447 -0.07462746]
5/5 [==============================] - 0s 2ms/step - loss: 0.1663
(略)
Epoch 20/20
layer1: [ 0.00553192  0.213019   -0.1658938   0.21581025 -0.08234034 -0.2084046 ]
5/5 [==============================] - 0s 2ms/step - loss: 0.0026

可以看到模型 loss 從0.1663降到0.0026，模型權重的差異性也蠻大的，0.07604259到0.00553192降低0.07左右，0.08207107到0.21581025升高了0.13左右，代表模型有學到東西！

測試 Input:

print(f'1={model.predict([1])[0]}, 2={model.predict([2])[0]}, 3={model.predict([3])[0]}')

1=[0.98057926], 2=[1.9300488], 3=[2.8795183]

要模型預測比1還大的數字也ok，不會差太多。

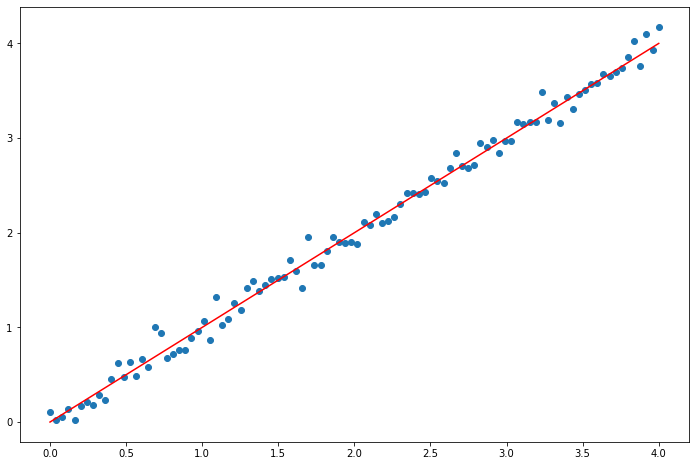
實驗二：資料集是100個從0到4的小數，產生梯度爆炸

x = np.linspace(0,4,100, dtype=np.float32)  # 介於[0,+4]之間的樣本
noise = np.random.normal(0, 0.1, x.shape).astype(np.float32)  # noise取樣本區間的5%, (4-0)*0.05=0.1
y = x
z = x + noise 

fig = plt.figure(figsize=(12,8))
plt.scatter(x,z)
plt.plot(x,y,color='red') 
plt.show()

train_data = tf.data.Dataset.from_tensor_slices((z,y))

ds_train = train_data.cache()
ds_train = ds_train.shuffle(SHUFFLE_SIZE)
ds_train = ds_train.batch(BATCH_SIZE)
ds_train = ds_train.prefetch(tf.data.experimental.AUTOTUNE)

產出：

Epoch 1/20
layer1: [-0.07210064  0.24890727  0.30479372 -0.30981055 -0.08024356 -0.16160044]
5/5 [==============================] - 0s 2ms/step - loss: 57269209748267820971597475348480.0000
Epoch 2/20
layer1: [ 6.2245629e+22  1.1131139e+23  1.2879328e+22 -1.5327043e+23
 -7.5734576e+22 -1.5577560e+23]
5/5 [==============================] - 0s 2ms/step - loss: nan
Epoch 3/20
layer1: [nan nan nan nan nan nan]
5/5 [==============================] - 0s 2ms/step - loss: nan
(略)

可以看到模型第一個 epoch 結束時，loss 已經是天文數字，第二個 epoch 開始前，模型的權重也高到10的22次方，所以後面直接炸掉變nan，我這邊讓他爆炸的主因是我沒有將資料做正規化，而模型有只有簡單的 dense layer，所以輸入乘上權重得出很大的值，再遇上 loss 計算就爆了！

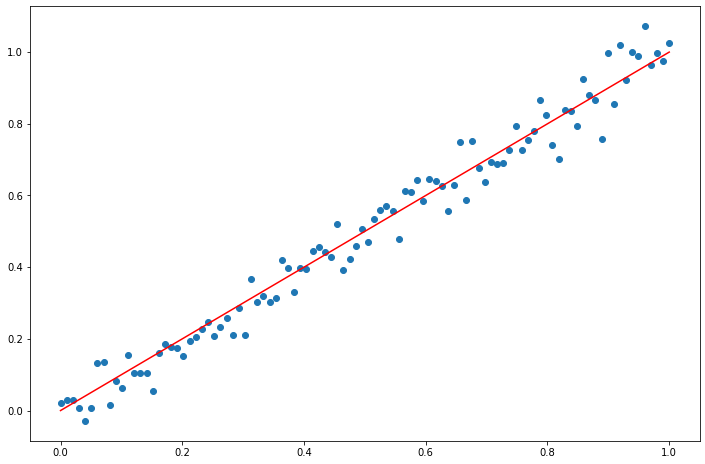
實驗三：資料集是100個從0到1的小數，產生梯度消失。

x = np.linspace(0,1,100, dtype=np.float32)  # 介於[0,1]之間的樣本
noise = np.random.normal(0, 0.05, x.shape).astype(np.float32)  # noise取樣本區間的5%, (1-0)*0.05=0.05
y = x
z = x + noise 

fig = plt.figure(figsize=(12,8))
plt.scatter(x,z)
plt.plot(x,y,color='red') 
plt.show()

train_data = tf.data.Dataset.from_tensor_slices((z,y))

ds_train = train_data.cache()
ds_train = ds_train.shuffle(SHUFFLE_SIZE)
ds_train = ds_train.batch(BATCH_SIZE)
ds_train = ds_train.prefetch(tf.data.experimental.AUTOTUNE)

ACT='sigmoid' # you can also try ACT=None or ACT='relu'

model = tf.keras.Sequential()
model.add(tf.keras.layers.Dense(32, activation=ACT, input_shape=(1,))) 
model.add(tf.keras.layers.Dense(32, activation=ACT))
model.add(tf.keras.layers.Dense(32, activation=ACT)) 
model.add(tf.keras.layers.Dense(32, activation=ACT)) 
model.add(tf.keras.layers.Dense(1))
model.compile(loss=tf.keras.losses.mean_squared_error, 
              optimizer=tf.keras.optimizers.SGD(learning_rate=0.1))

history = model.fit(
    ds_train,
    epochs=EPOCHS,
    verbose=True,
    callbacks=[PrintWeightsCallback()])

這邊的ACT也推薦大家試試 None 或 'relu' 看看不一樣的效果。

產出：

Epoch 1/20
layer1: [ 0.18758693 -0.0771921  -0.01569629  0.17212537  0.1411779   0.10927829]
5/5 [==============================] - 0s 3ms/step - loss: 0.5679
Epoch 2/20
layer1: [ 0.18786529 -0.07689717 -0.01544899  0.17244542  0.14150831  0.10956431]
5/5 [==============================] - 0s 2ms/step - loss: 0.1452
(略)
Epoch 20/20
layer1: [ 0.18772912 -0.07688259 -0.01586881  0.17269064  0.14184701  0.10949538]
5/5 [==============================] - 0s 3ms/step - loss: 0.0864

可以看到 loss 雖有從0.5679下降到0.0864，但是權重值的變化量幾乎沒有改變。

測試 Input:

print(f'1={model.predict([1])[0]}, 2={model.predict([2])[0]}, 3={model.predict([3])[0]}')

1=[0.5729448], 2=[0.5735199], 3=[0.5740514]

實測把1,2,3丟到模型裡推論，拿到的結果都是0.57，和實驗一對比，實驗三的 sigmoid 設計產生了梯度消失。