前言：上一篇講完了排序的基本定義和最普遍的氣泡排序，接著要繼續介紹更多新的排序。

插入排序法：

和氣泡排序一樣也是分常簡單直觀的一種排序，如果有已經排序好的資料要加資料時，就適合使用插入排序，只要按照鍵值從小排到大就可以了。這樣的過程很像我們在玩撲克牌時整理手牌的過程，在發牌時，每一次拿到新的牌就會放到它適合的位子(由小到大)，這樣的做法就是插入排序喔！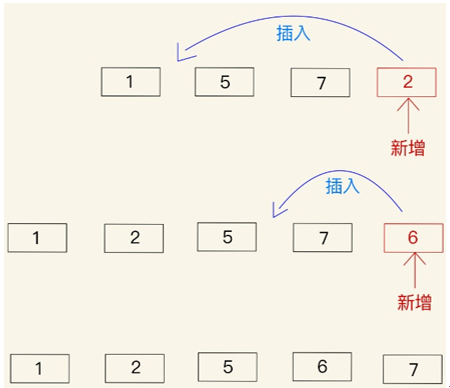

執行效率分析：
插入排序在排序n個資料時，第一層迴圈需要執行n-1次插入n-1個鍵值，第二層迴圈在最差的情況下需要執行1、2、3、…n-2、n-1次，所以合計次數為n(n-1)/2，執行效率為O(n^2)。

如果資料室已經排序好的情況下，只需插入資料(沒有搬移動作)，那只須執行外層迴圈的n-1次，執行效率為O(n)。

插入排序和氣泡排序一樣都不需要額外的記憶體，屬於穩定性的排序法，因為在資料搬移時，原位置的資料一定要比插入的元素大才會往後移，所以不會交換到相同鍵直的元素。

直接插入排序實作：依照搜尋插入的位置還能再細分直接插入排序和二分插入排序，就讓我們用時做來看看這兩者的差異吧。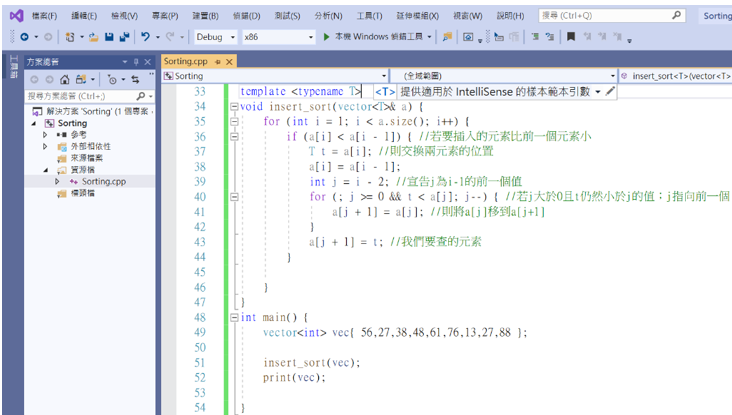

這樣就完成了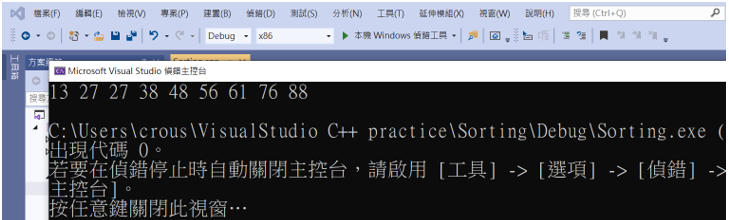

也可以查看排序過程和次數喔！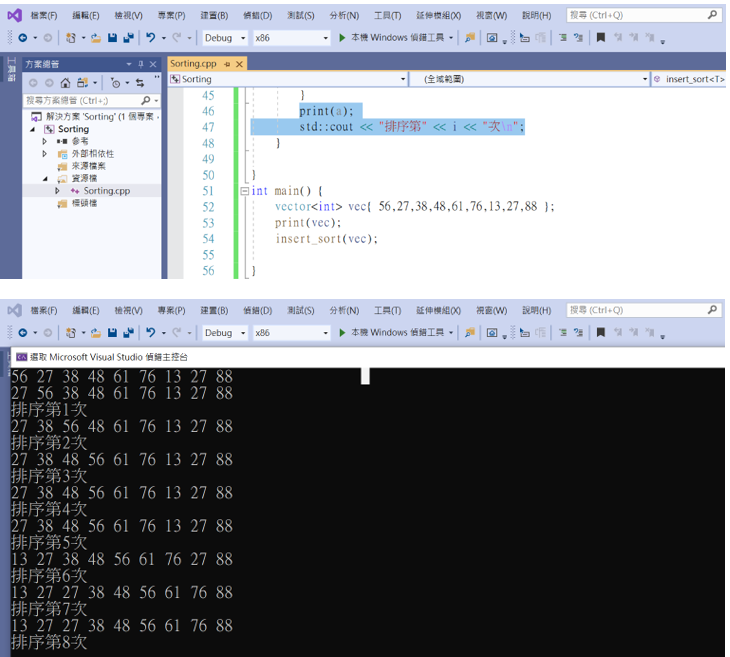

二分插入排序實作：算是插入排序比直接插入排序有效率一些，剛剛實作的直接插入排序是順著資料查詢要放在哪，二分插入排序是用二分法來查詢元素插入位置的過程。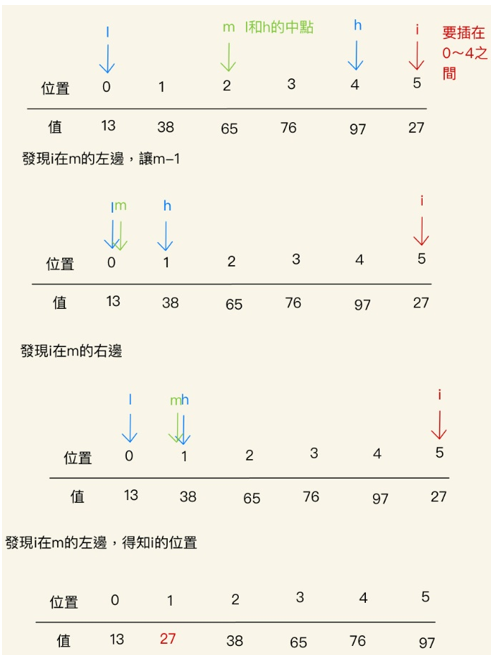

具體要怎麼做？直接來實作看看吧！

主要是l、h、m三個變數要如何交換或更改指標才是困難的點。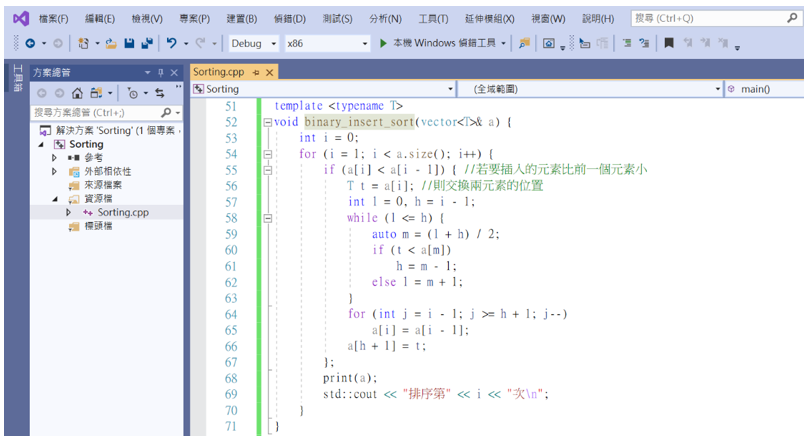

結果也與直接插入排序一樣，這樣程式就順利完成了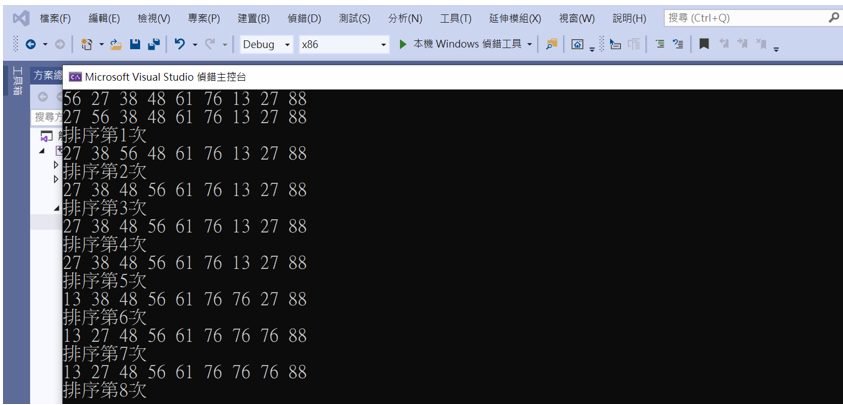

本日小結：今天講了兩種插入排序，如果二分插入排序很難理解的話，可以先把直接插入排序先弄懂就好，基礎還是比較重要。明天也要來講解謝爾排序和選擇排序v(=∩_∩=)

直接插入排序

template <typename T>
void insert_sort(vector<T>& a) {
	int i = 0;
	for (i = 1; i < a.size(); i++) {
		if (a[i] < a[i - 1]) { //若要插入的元素比前一個元素小
			T t = a[i]; //則交換兩元素的位置
			a[i] = a[i - 1];
			int j = i - 2; //宣告j為i-1的前一個值
			for (; j >= 0 && t < a[j]; j--) { //若j大於0且t仍然小於j的值；j指向前一個
				a[j + 1] = a[j]; //則將a[j]移到a[j+1]
			}
			a[j + 1] = t; //我們要查的元素
		}
		print(a);
		std::cout << "排序第" << i << "次\n";
	}
}

二分插入排序

template <typename T>
void binary_insert_sort(vector<T>& a) {
	int i = 0;
	for (i = 1; i < a.size(); i++) {
		if (a[i] < a[i - 1]) { //若要插入的元素比前一個元素小
			T t = a[i]; //則交換兩元素的位置
			int l = 0, h = i - 1;
			while (l <= h) {
				auto m = (l + h) / 2;
				if (t < a[m])
					h = m - 1;
				else l = m + 1;
			}
			for (int j = i - 1; j >= h + 1; j--)
				a[i] = a[i - 1];
			a[h + 1] = t;
		};
		print(a);
		std::cout << "排序第" << i << "次\n";
	}
}