前言：甚麼是基數排序法？在我剛剛接觸這個名詞的時候心中滿是問號，有很多排序法看到名稱或許就能猜出是怎麼運行的，但是卻完全摸不透基數排序，藉由這邊文章，讓我們來探討基數排序的秘密吧！

多關鍵字排序：

先來講講甚麼是多關鍵字排序，之前介紹到的排序法大多都只要一個關鍵字，有時候某些資料會存在多個關鍵字(例如撲克牌的數值和花色)，而多關鍵字排序能依優先方式分成兩種。

• 最高位優先 (Most Significant Digit First , MSD)
• 最低位優先 (Least Significant Digit First , LSD)
  以撲克牌當舉例，將數值大小設定為最高位，花色設定成最低位。
  MSD就是將相同數值的牌放在一起，共13堆。
  LSD則是將相同花色的牌放在一起，共分4堆。
  注意！！！每個關鍵字必須是穩定的，不然排序會整個亂掉。

基數排序：

是一種非比較型整數排序演算法，原理是將整數按位元數切割成不同的數字，然後按每個位數分別比較。操作方法可以想像成將二位數值寫在一堆卡片上，先依十位數牌成十堆卡片，然後在每一堆卡片依照個位數進行排序，最後將十堆卡片依序堆好來完成排序。
如果要排序的資料有位數不等的情況下，先將位數較短的數前面補0，然後從最低位開始依次進行一次排序，這樣從最低位排序一直到最高位排序完成以後，數列就變成一個有序序列。
由於整數也可以表達字串（比如名字或日期）和特定格式的浮點數，所以基數排序也不是只能使用於整數。
參考資料：https://zh.wikipedia.org/wiki/%E5%9F%BA%E6%95%B0%E6%8E%92%E5%BA%8F

基數排序的MSD：分別依序從百位、十位，最後到個位數進行排序。
基數排序的LSD：分別依序從個位、十位，最後到百位數進行排序。

執行效率分析：基數排序的執行效率和快速排序非常相像，以n個鍵值來說，在二層迴圈的內層是O(n)，外層最多執行Log n次，所以時間複雜度是O(n Log n)。
基數排序需要佇列的額外記憶體作為儲存空間使用。是一種穩定性的排序法，因為元素是存入佇列，佇列先進先出的特性並不會交換到相同鍵值的元素。

基數排序實作：基數排序比較複雜，可以重建一個資源檔方便撰寫。

這次採用系統取亂數的方法來選定要排序的數值。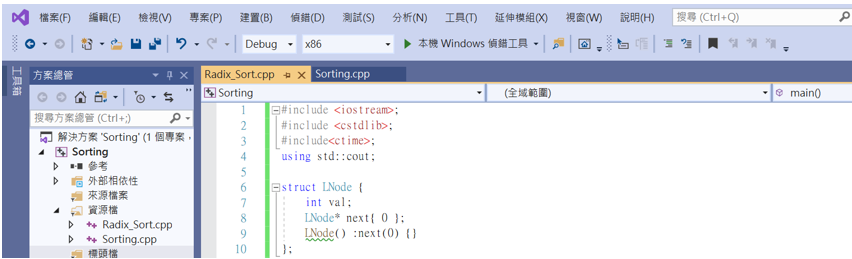

首先是基數排序過程的函式。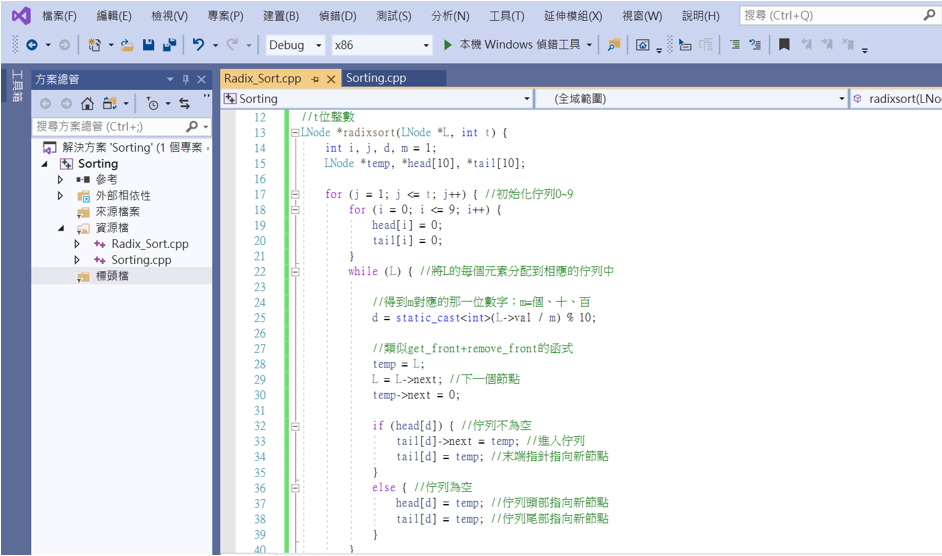

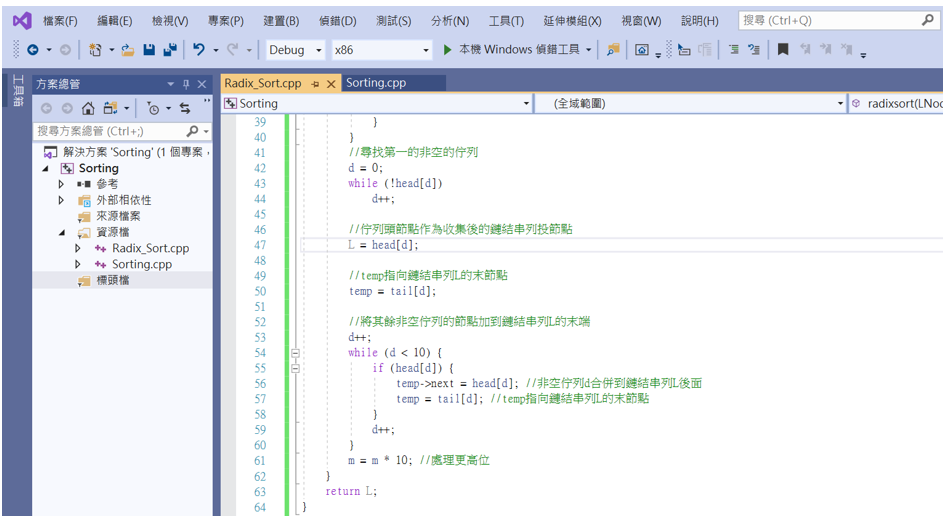
再來式主程式內容。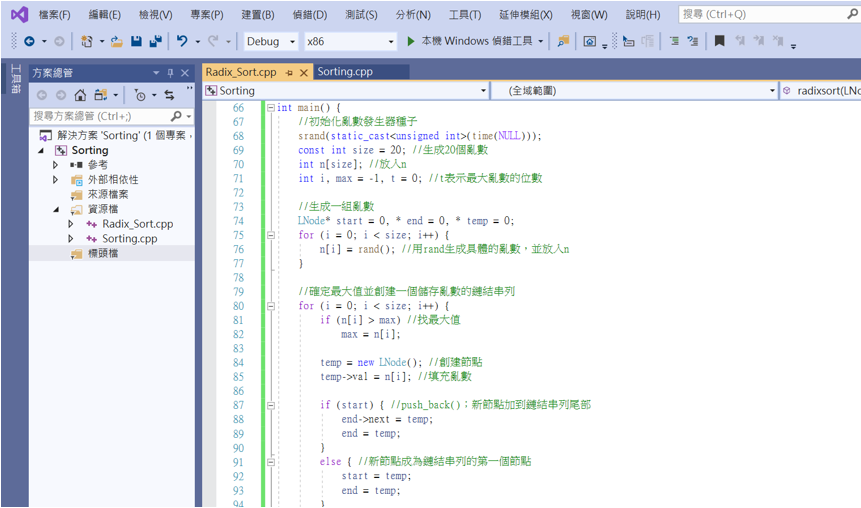

最後附上執行結果。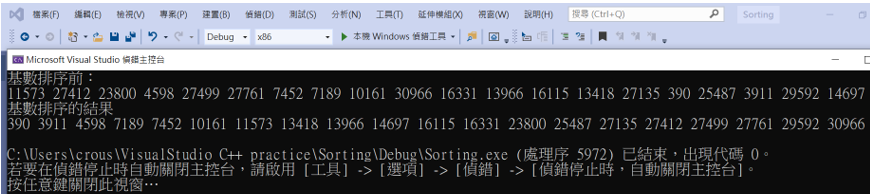

本日小結：以往都是自己創建數列來排序，這次用比較不一樣的系統取亂數來表示，但也不算是太複雜的東西，主要還是難在基數排序和以往的排序法不太一樣，以往的排序都是互相比較，基數排序有點像是對每個數分類，分類到最後才排序出結果，這一部分就複雜很多了，當初用鏈結串列實作的時候，也是對了超久，好險最後還是有成功做出來，下一篇要來講解最後一個桶排序和對至今講過的排序法做一個比較٩(●˙▿˙●)۶…⋆ฺ

#include <iostream>;
#include <cstdlib>;
#include<ctime>;
using std::cout;

struct LNode {
	int val;
	LNode* next{ 0 };
	LNode() :next(0) {}
};

//t位整數
LNode *radixsort(LNode *L, int t) {
	int i, j, d, m = 1;
	LNode *temp, *head[10], *tail[10];

	for (j = 1; j <= t; j++) { //初始化佇列0~9
		for (i = 0; i <= 9; i++) {
			head[i] = 0;
			tail[i] = 0;
		}
		while (L) { //將L的每個元素分配到相應的佇列中

			//得到m對應的那一位數字；m=個、十、百
			d = static_cast<int>(L->val / m) % 10;

			//類似get_front+remove_front的函式
			temp = L;
			L = L->next; //下一個節點
			temp->next = 0;

			if (head[d]) { //佇列不為空
				tail[d]->next = temp; //進入佇列
				tail[d] = temp; //末端指針指向新節點
			}
			else { //佇列為空
				head[d] = temp; //佇列頭部指向新節點
				tail[d] = temp; //佇列尾部指向新節點
			}
		}
		//尋找第一的非空的佇列
		d = 0;
		while (!head[d]) 
			d++;

		//佇列頭節點作為收集後的鏈結串列投節點
		L = head[d]; 

		//temp指向鏈結串列L的末節點
		temp = tail[d];
		
		//將其餘非空佇列的節點加到鏈結串列L的末端
		d++;
		while (d < 10) {
			if (head[d]) {
				temp->next = head[d]; //非空佇列d合併到鏈結串列L後面
				temp = tail[d]; //temp指向鏈結串列L的末節點
			}
			d++;
		}
		m = m * 10; //處理更高位
	}
	return L;
}

int main() {
	//初始化亂數發生器種子
	srand(static_cast<unsigned int>(time(NULL)));
	const int size = 20; //生成20個亂數
	int n[size]; //放入n
	int i, max = -1, t = 0; //t表示最大亂數的位數
	
	//生成一組亂數
	LNode* start = 0, * end = 0, * temp = 0;
	for (i = 0; i < size; i++) {
		n[i] = rand(); //用rand生成具體的亂數，並放入n
	}

	//確定最大值並創建一個儲存亂數的鏈結串列
	for (i = 0; i < size; i++) {
		if (n[i] > max) //找最大值
			max = n[i];

		temp = new LNode(); //創建節點
		temp->val = n[i]; //填充亂數

		if (start) { //push_back()；新節點加到鏈結串列尾部
			end->next = temp;
			end = temp;
		}
		else { //新節點成為鏈結串列的第一個節點
			start = temp;
			end = temp;
		}
	}
	while (max > 0) { //確定最大亂數的位數t
		t = t + 1;
		max = max / 10;
	}
	cout << "基數排序前： \n";
	temp = start;
	//for (i = 0; i < size; i++) {
	while (temp) {
		cout << temp->val << " ";
		temp = temp->next;
	}
	cout << "\n";
	//基數排序
	start = radixsort(start, t);

	cout << "基數排序的結果\n";
	temp = start;
	//for (i = 0; i < size; i++) {
	while(temp){
		cout << temp->val << " ";
		temp = temp->next;
	}
	cout << "\n";
	return 0;
}