前言：今天要來介紹的兩個排序法，是基礎排序的最後兩個，讓我們來看看它們的特點吧！

選擇排序法：

也是相當直觀簡單的排序法，只要從一整個排序中選出鍵值最小的，然後和第一個鍵值做交換，接著從剩下的鍵值中選出第二小的和第二個交換鍵值，重複執行直到最後一個鍵值為止。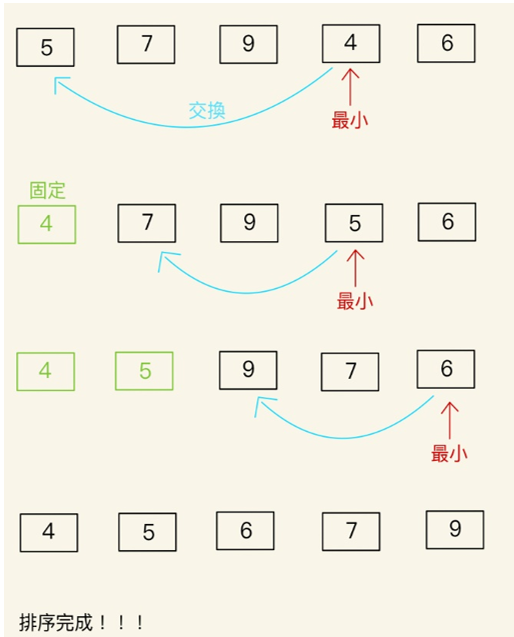

執行效率分析：和氣泡排序一樣，第一層迴圈需要執行n-1次，n是全部排序鍵值的個數，第二層迴圈依序為n-1、n-2、….2、1、0，總次數為n(n-1)/2，時間複雜度為O(n^2)。
不需要額外的記憶體，是一種不穩定的排序，因為元素在交換時可能會交換到相同鍵直的元素。

選擇排序實作：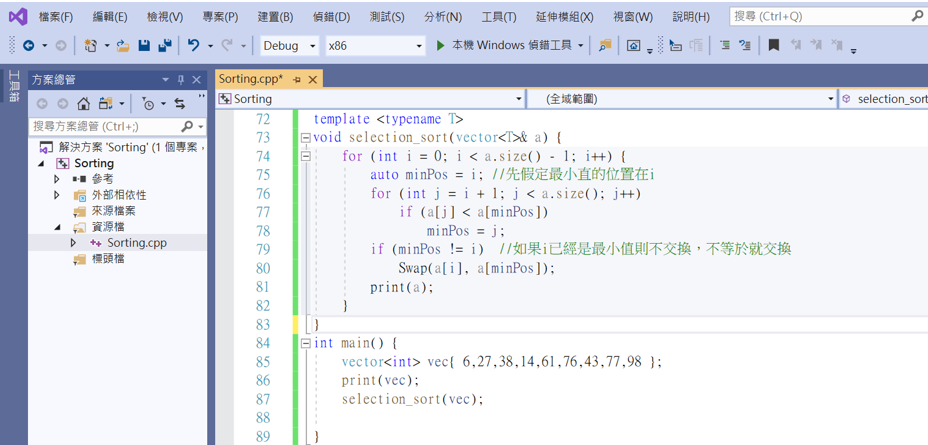

這樣就完成囉！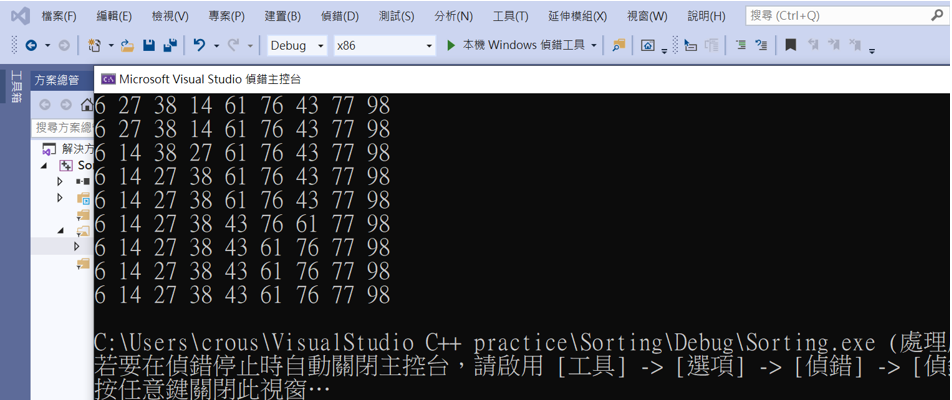

謝爾排序法：

謝爾排序和上一篇講到的插入排序原理非常相似，以插入排序的優點來提升排序效率，是插入排序的改良版。接著用圖解說明一下操作概念。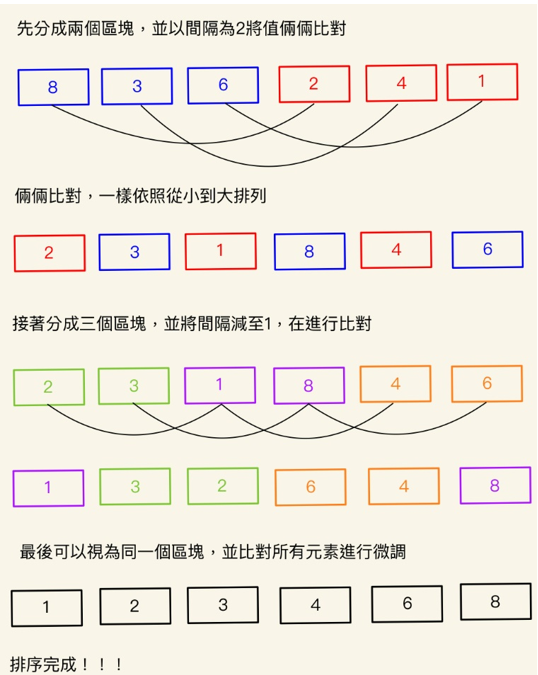

執行效率分析：間隔的可以說是希爾排序最重要的一環，不同的間隔序列會造成不同的效率，常見的可分為三種間隔序列。

謝爾排序法不需要額外的記憶體空間，但是不具有穩定性，因為在排序時會進行分割，然後分別執行插入排序，所以有可能會交換到相同間值的元素。

謝爾排序實作：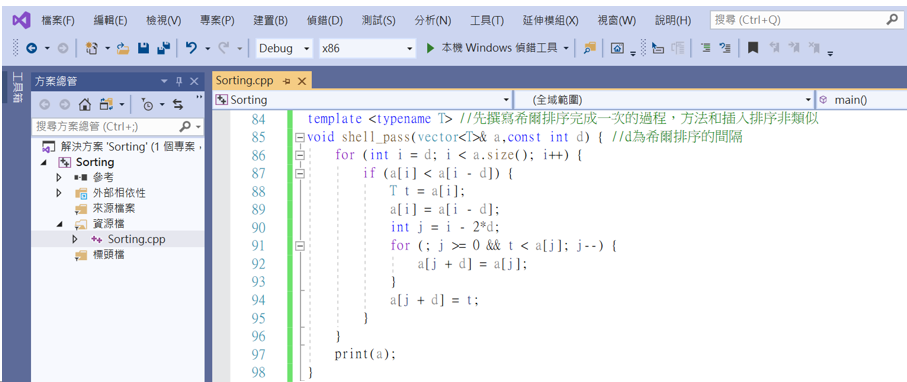

第一行為間隔=5的排序，第二行為間隔=3的排序，第二行為間隔=1的排序，排序過程沒有異常，而且效率非常高！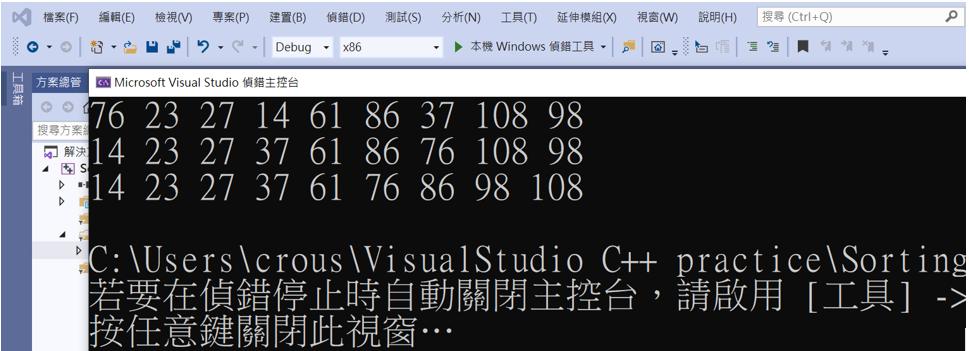

本日小結：今天包含前兩篇文章就結束了基礎排序法的部分，選擇排序和希爾排序的難度都不高，相信大家一定能很快吸收，接下來的排序法會是複雜一點的分割資料的排序法，共有兩種等著大家來攻略(^人^)

選擇排序法

template <typename T>
void selection_sort(vector<T>& a) {
	for (int i = 0; i < a.size() - 1; i++) {
		auto minPos = i; //先假定最小直的位置在i
		for (int j = i + 1; j < a.size(); j++)
			if (a[j] < a[minPos])
				minPos = j;
		if (minPos != i)  //如果i已經是最小值則不交換，不等於就交換
			Swap(a[i], a[minPos]);
		print(a);
	}
}

謝爾排序法

template <typename T> //先撰寫希爾排序完成一次的過程，方法和插入排序非類似
void shell_pass(vector<T>& a,const int d) { //d為希爾排序的間隔
	for (int i = d; i < a.size(); i++) {
		if (a[i] < a[i - d]) { 
			T t = a[i]; 
			a[i] = a[i - d];
			int j = i - 2*d; 
			for (; j >= 0 && t < a[j]; j--) { 
				a[j + d] = a[j]; 
			}
			a[j + d] = t; 
		}
	}
	print(a);
}
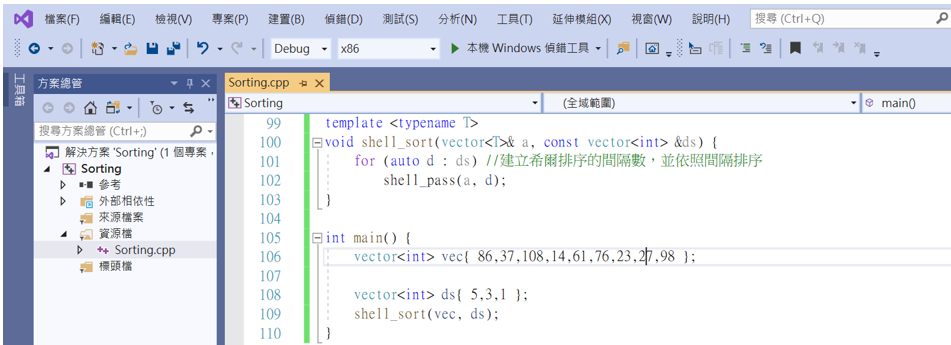
template <typename T> 
void shell_sort(vector<T>& a, const vector<int> &ds) {
	for (auto d : ds) //建立希爾排序的間隔數，並依照間隔排序
		shell_pass(a, d);
}