前言：今天要來介紹第二種分割資料的排序法，就讓我們來看看這個有趣的排序法吧！

合併排序：

首先會將一筆資料分割成兩部分，然後再將這兩部分對半切，直到切到資料的最小單位，之後從小單位開始整合排序，在逐漸合併成排序好的資料。可以重新安排一線性串列成為指定順序的資料，是一種外部儲存裝置最常使用的排序方法，因為儲存在硬碟或循序檔案上的資料就是一種線性串列。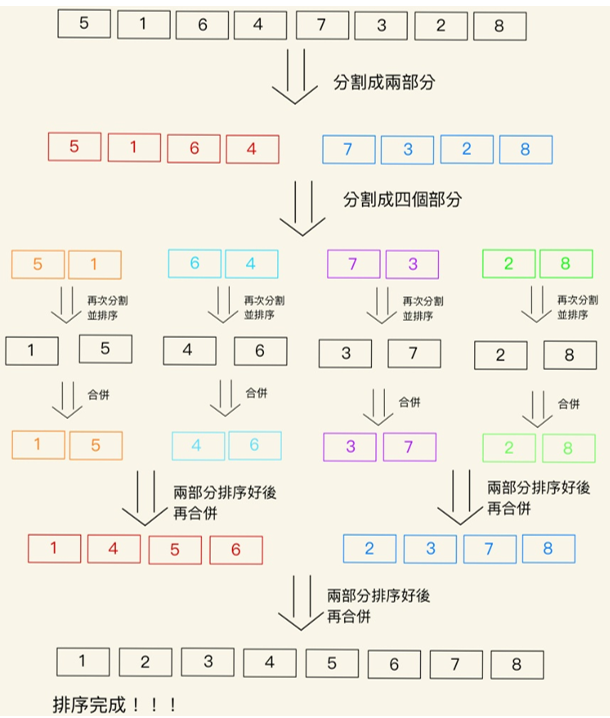

執行效率分析：合併排序的執行效率分成兩部分，在合併部分和排序鍵直數成正比，時間複雜度為O(n)；分割部分每次會分二分之一，處理次數大概為Log n次完成排序，綜合兩次執行其時間複雜度為O(n Log n)。

合併排序需要使用遞迴函式，所以要有額外的記憶體空間來處理遞迴方法。是一種具有穩定性的排序法，因為只有在合併時會交換元素，所以不會交換到相同鍵值的元素。

合併排序實作：在寫好排序法之前，先來實現如何將兩組以排序好的數列合併且整理好，這是合併排序的第一步。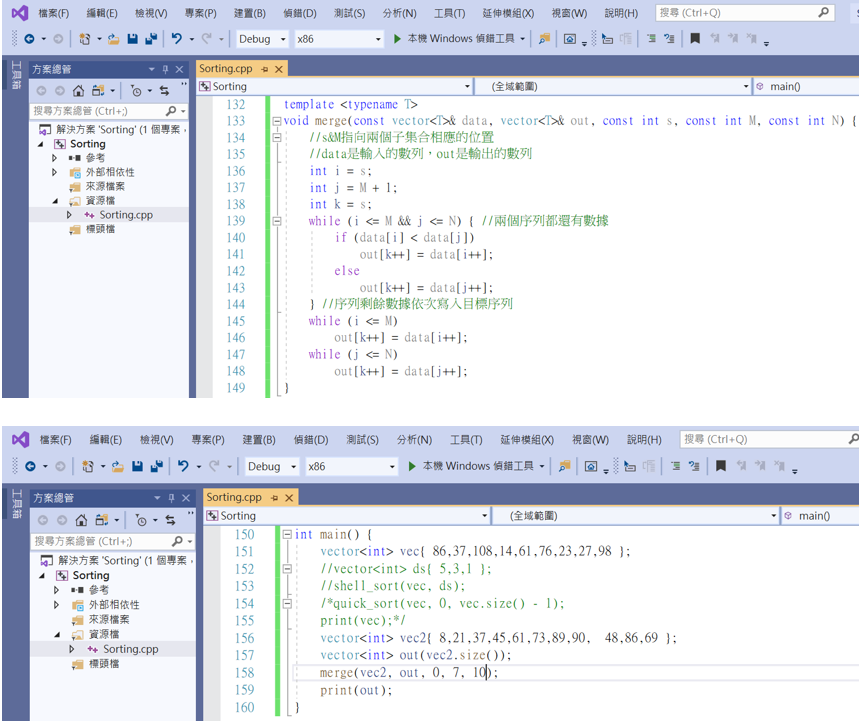

將0~7(共8個元素)的序列，和後面3個元素合併成大小為10的序列。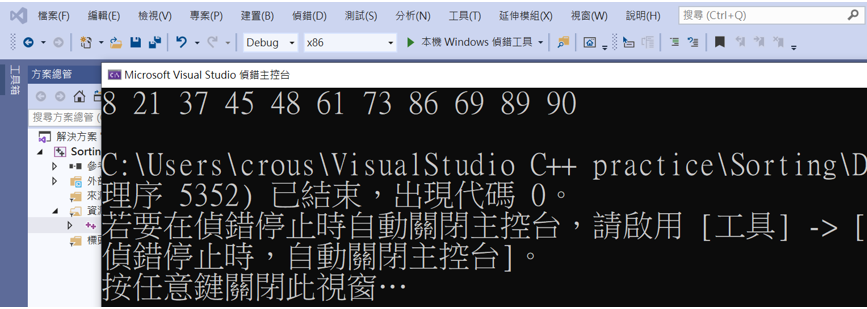

完成此步驟後就可以來撰寫合併排序了。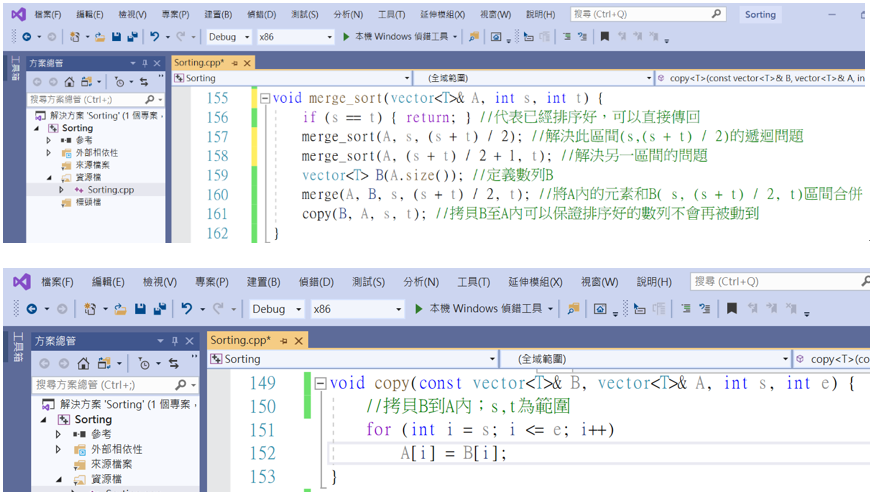

這樣就排序成功了喔！

本日小結：這樣就介紹完了兩個高等的分割資料排序，合併排序法只要分割至最小部分，然後倆倆經過排序再合併成一個數列就完成了，合併時的程式比較複雜也很容易在那邊出錯，設計的程式的時候要格外小心。鐵人賽也已經接近尾聲，之後的篇幅也會著重介紹其他的排序法和實作給大家看，剩下最後幾天大家一起加油吧୧| ⁰ ᴥ ⁰ |୨

template <typename T>
void merge(const vector<T>& data, vector<T>& out, const int s, const int M, const int N) {
	//s&M指向兩個子集合相應的位置
	//data是輸入的數列，out是輸出的數列
	int i = s, j = M + 1, k = s;
	while (i <= M && j <= N) { //兩個序列都還有數據
		if (data[i] < data[j]) 
			out[k++] = data[i++];
		else
			out[k++] = data[j++];
	} //序列剩餘數據依次寫入目標序列
	while (i <= M) 
		out[k++] = data[i++];
	while (j <= N) 
		out[k++] = data[j++];
}

template <typename T>
void copy(const vector<T>& B, vector<T>& A, int s, int e) {
	//拷貝B到A內；s,t為範圍
	for (int i = s; i <= e; i++)
		A[i] = B[i];
}

template <typename T>
void merge_sort(vector<T>& A, int s, int t) {
	if (s == t) { return; } //代表已經排序好，可以直接傳回
	merge_sort(A, s, (s + t) / 2); //解決此區間(s,(s + t) / 2)的遞迴問題
	merge_sort(A, (s + t) / 2 + 1, t); //解決另一區間的問題
	vector<T> B(A.size()); //定義數列B
	merge(A, B, s, (s + t) / 2, t); //將A內的元素和B( s, (s + t) / 2, t)區間合併
	copy(B, A, s, t); //拷貝B至A內可以保證排序好的數列不會再被動到
}