前言：桶排序又名箱排序，究竟這個特殊的排序法是怎麼運作的，讓我們一來探討！

桶排序：

和上一篇的基數排序一樣是非比較型的排序法。運作原理通常是會先建立一些用來存放資料的桶子，每個桶子都有對應的資料區間，再將待排序的元素分別放到對應區間的桶內，並在桶內進行排序(在桶內的排序可以使用其他排序法，又或著可以用遞迴的方式繼續執行桶排序)，最後在把桶內的元素取出就完成了，換言之，桶排序是用分析鍵值的分布來排序的。

執行效率分析：如果共有n個元素需要排序，而這些元素剛好都分散在不同的桶子中，也就是不必在桶內進行額外的排序，這實是最理想的狀況，時間複雜度為O(n+m)(m用來表示桶子的數量)；但如果所有的元素都在一個桶內，則為最差的情況，時間複雜度為O(n^2)。

必須使用桶來暫時存放資料，所以需要用到額外的記憶體空間。屬於穩定性的排序法，因為元素要分別放入桶內進行排序，所以相同鍵值的元素，排序後相對位置不會改變。

桶排序實作：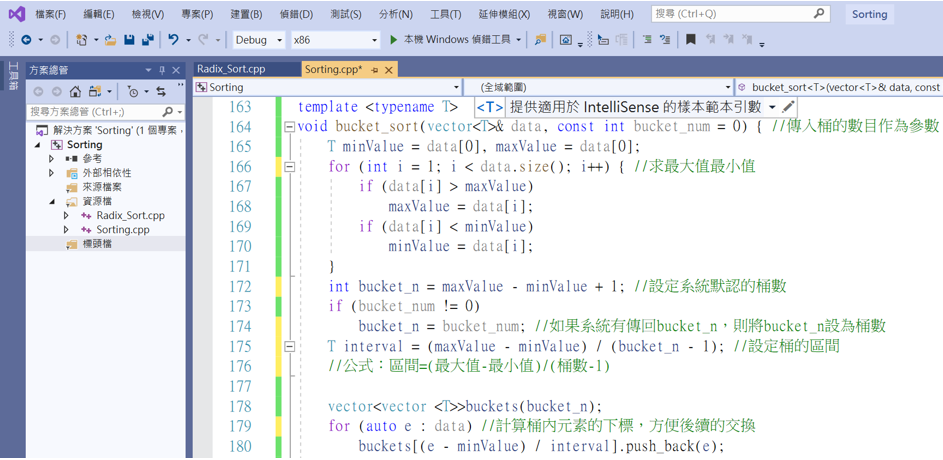

可以看到成功輸出兩組數組，負數也能在排序範圍。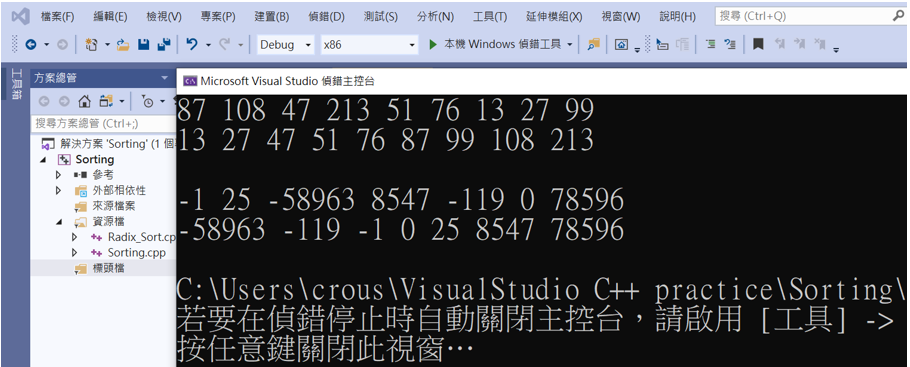

各排序法的比較：最後來複習並比較一下有介紹過的排序法。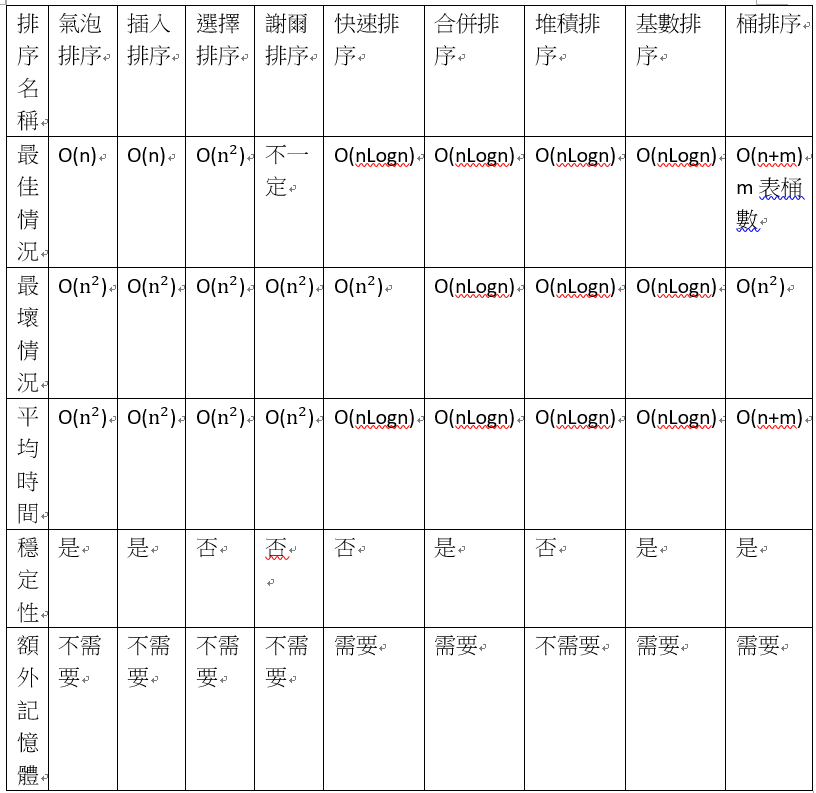

本日小結：總算完結了排序的部分，其實排序法遠遠不止這些，這些是在課堂上比較有接觸到的才分享給大家，如果還有參加鐵人賽，或許還有機會跟大家一起討論，明天就沒有要在講新的東西了，純粹跟大家分享鐵人賽的心得和感想，感謝大家看到最後（〃＾∇＾）o

template <typename T>
void bucket_sort(vector<T>& data, const int bucket_num = 0) { //傳入桶的數目作為參數
	T minValue = data[0], maxValue = data[0];
	for (int i = 1; i < data.size(); i++) { //求最大值最小值
		if (data[i] > maxValue)
			maxValue = data[i];
		if (data[i] < minValue)
			minValue = data[i];
	}
	int bucket_n = maxValue - minValue + 1; //設定系統默認的桶數
	if (bucket_num != 0)
		bucket_n = bucket_num; //如果系統有傳回bucket_n，則將bucket_n設為桶數
	T interval = (maxValue - minValue) / (bucket_n - 1); //設定桶的區間
	//公式：區間=(最大值-最小值)/(桶數-1)

	vector<vector <T>>buckets(bucket_n);
	for (auto e : data) //計算桶內元素的下標，方便後續的交換
		buckets[(e - minValue) / interval].push_back(e);

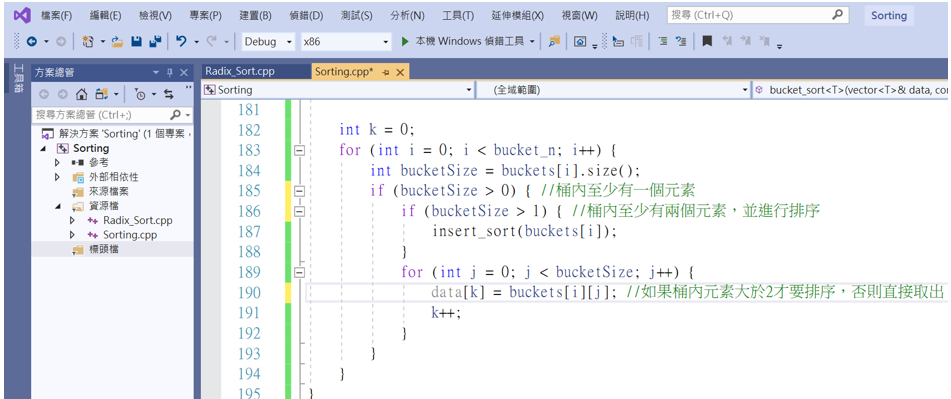
	int k = 0;
	for (int i = 0; i < bucket_n; i++) {
		int bucketSize = buckets[i].size();
		if (bucketSize > 0) { //桶內至少有一個元素
			if (bucketSize > 1) { //桶內至少有兩個元素，並進行排序
				insert_sort(buckets[i]);
			}
			for (int j = 0; j < bucketSize; j++) {
				data[k] = buckets[i][j]; //如果桶內元素大於2才要排序，否則直接取出
				k++;
			}
		}
	}
}