前言：在第16、17天的時候有介紹到堆積，今天要利用堆積的特性來實現排序法，忘記或不知道堆積是甚麼的人可以回去這兩篇看看。

堆積排序：
快速幫大家複習一下，堆積是一顆完整二元樹，且堆積的父節點都比其左右子節點的資料大或相等，而堆積排序就是一種樹狀結構的排序法，最主要的工作就是建立「堆積」。
建立好堆積後就可以開始執行堆積排序，操作步驟可以大致分成三個階段

1. 從二元樹調整節點或建立成堆積。
2. 在輸出堆積的根節點後，將剩下的二元樹節點重建成堆積。
3. 重複操作直到所有節點輸出。
   

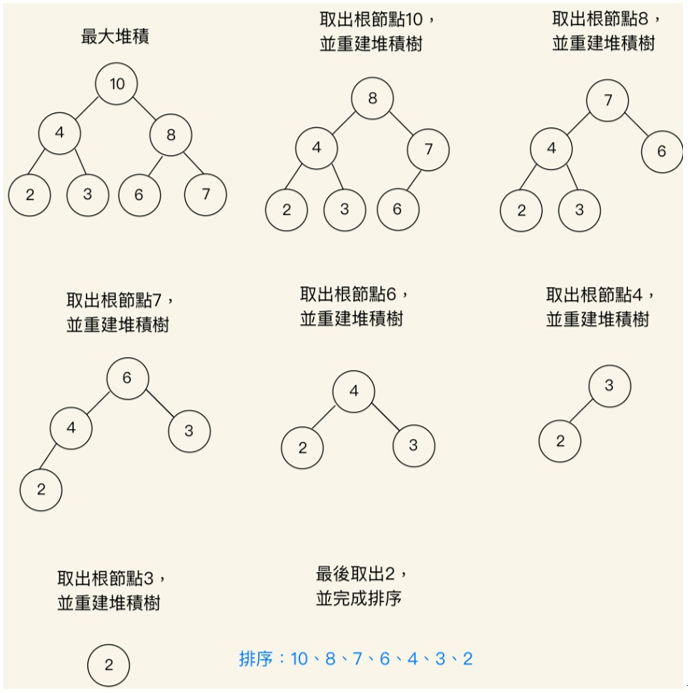
執行效率分析：堆積排序法的執行效率是當排序的資料個數為n時，堆積排序的主迴圈一共執行n-1次，每次執行的效率為樹高(即Log n)，可以得知時間複雜度為O(n Log n)。

堆積排序法不需要額外的記憶體空間，不過這種排序法並不穩定，因為在調節根節點時，可能會交換到相同件值得元素。

堆積排序實作：這次的排序會實作在之前堆積的檔案，因為有很多已經寫好的函示會使用到，大家可以先把堆積實作的檔案找出來。

首先要來修改之前向下調整的函式。
如果不想改原來的程式，可以先複製下來然後照著上面改，但是函式名稱要修改，不然程式會不知道要執行哪個向下調整的方法。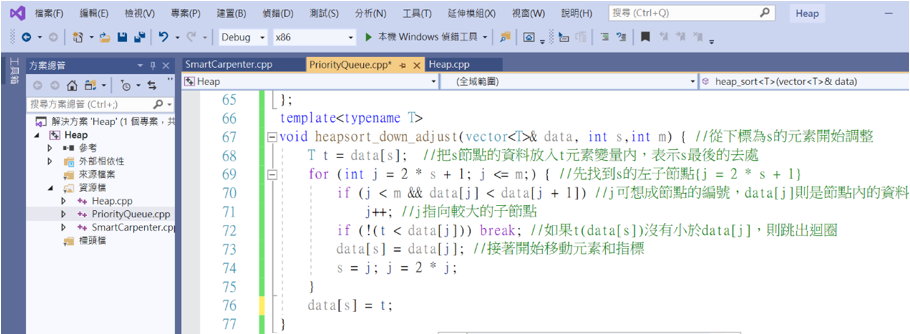

接著是堆積排序的主要執行方法。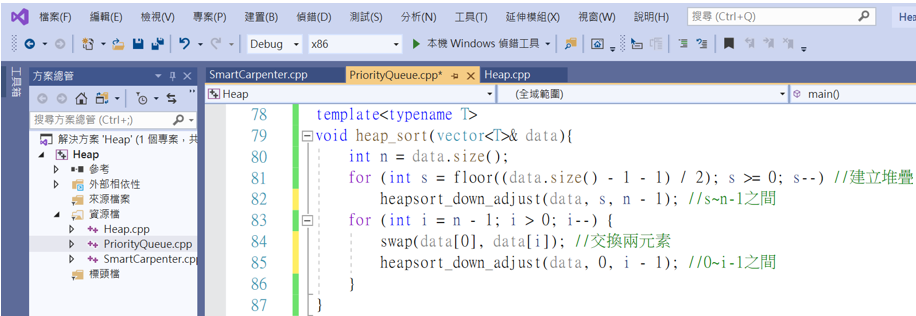

最後來看看執行結果。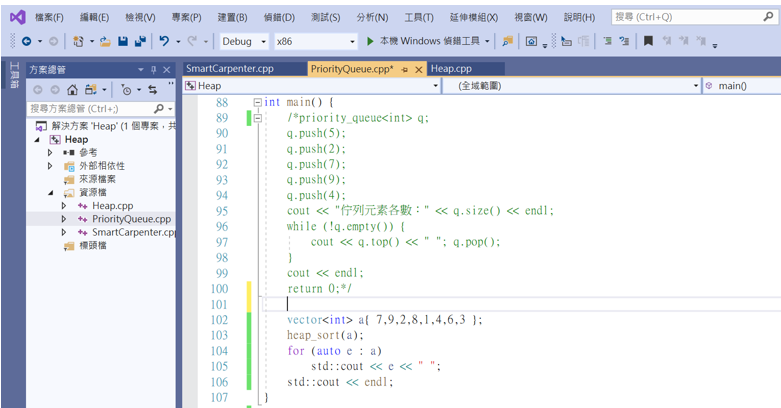

這樣堆積排序就完成了。

本日小結：堆積排序法的執行速度在各排序法中也是佼佼者，但是因為堆積需要使用到樹狀結構，不僅架構時比較麻煩，如果之後有出錯或需要維護的話也會稍嫌困難，在撰寫程式時，這些問題都是必須要納入考量的。雖然這麼說好像很複雜似的，但是簡單的堆積排序其實只要使用一般的陣列就可以時做出來，就如同今天的實作一樣，下一篇要來介紹基數排序法(^・ω・^ )

template<typename T>
void heapsort_down_adjust(vector<T>& data, int s,int m) { //從下標為s的元素開始調整
	T t = data[s];  //把s節點的資料放入t元素變量內，表示s最後的去處
	for (int j = 2 * s + 1; j <= m;) { //先找到s的左子節點{j = 2 * s + 1}
		if (j < m && data[j] < data[j + 1]) //j可想成節點的編號，data[j]則是節點內的資料
			j++; //j指向較大的子節點
		if (!(t < data[j])) break; //如果t(data[s])沒有小於data[j]，則跳出迴圈
		data[s] = data[j]; //接著開始移動元素和指標
		s = j; j = 2 * j;
	}
	data[s] = t;
}

template<typename T>
void heap_sort(vector<T>& data){
	int n = data.size();
	for (int s = floor((data.size() - 1 - 1) / 2); s >= 0; s--) //建立堆疊
		heapsort_down_adjust(data, s, n - 1); //s~n-1之間
	for (int i = n - 1; i > 0; i--) {
		swap(data[0], data[i]); //交換兩元素
		heapsort_down_adjust(data, 0, i - 1); //0~i-1之間
	}
}