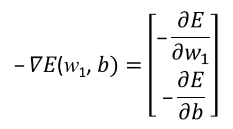上一篇有提到關於如何在向量中求梯度下降的公式，
因此此篇要來講為什麼要向量v跟f(x,y)的偏微分作內積：

• Properties of the Directional Derivative

首先我們已經知道內積可以有兩種算法：
假設現在有 A[a1,a2] 和 B[b1,b2] 要作內積，

1. 直接爆開互乘，A dot B = a1 * b1 + a2 * b2
2. 長度 * A和B之間的cos夾角，A dot B = |A| * |B| * cosΘ

在這邊我們要使用的是第二種方式，
首先假設我們知道公式是，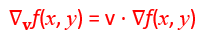
也就是v跟f(x,y)的偏微分作內積，
因此把它展開看可以知道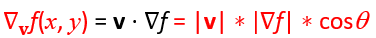

v在這邊不重要，因為v只是代表我們在那個向量v帶入時所得到的梯度下降，所以這邊就先假設他是1，可以得到：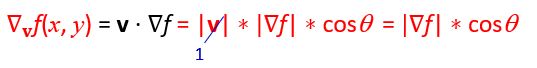

現在可以知道當我們要求出梯度上升的極大值的話，唯一的變數就是cosΘ，而當 Θ = 0°時會有最大值cosΘ = 1，
也就是說當向量v跟f(x,y)重疊時，會有最大的上升值。

相反的，當我們要校正它並測量梯度下降的時候， Θ = 180°時會有最大值cosΘ = -1，
也就是說當向量v向量v跟f(x,y)相反方向時，會有最大的下降值。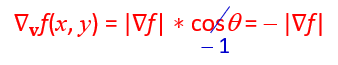

• Gradient Descent of Error Function

於是當我們要透過梯度下降找到最小值的Error Function時，便會採用，
也就是透過對E(w,b)作偏微分，找到error function自己的梯度關係曲線。